Экспериментальное определение сопротивления промежуточ­ных скреплений повороту рельсов относительно шпал

Цикл статей:
Глава 1 – Зависимость устойчивости бесстыкового пути от типов промежуточных рельсовых скреплений и условий их эксплуатации

Глава 2 – Экспериментальное определение сопротивления промежуточ­ных скреплений повороту рельсов относительно шпал

Глава 3 – Оценка устойчивости бесстыкового пути в зависимости от вида и условий эксплуатации промежуточных рельсовых скреплений методом дифференциальных уравнений равновесия

Глава 4 – Определение критических параметров оценки устойчивости бесстыкового пути

От того, насколько верны все основные элементы намечаемых и проводившихся экспериментов, зависят, эксплуатационные нормы уст­ройства и содержания бесстыкового пути, области их применения, техно­логии работ при ремонтах и содержании пути и другие важные практиче­ские решения.

Все методики выполнения экспериментальных исследований нату­ральных конструкций бесстыкового пути, разработанные Е.М. Бромбер- гом, использовались во ВНИИЖТе. Более того, полученные результаты испытаний используются и теперь в нормативных документах МПС по устройству и содержанию бесстыкового пути [28].

Методика определения сопротивления промежуточных скреплений повороту рельса в горизонтальной плоскости заключается в приложении к фрагменту рельса крутящего момента в горизонтальной плоскости на уровне нейтральной оси рельса и регистрации возникающего угла поворо­та рельса относительно шпалы, так как в аналитических методах оценки устойчивости пути рассматриваются уравнения, описывающие продольно- поперечные деформации нейтральной оси рельсовых нитей [22]. Искомую зависимость можно получить, осуществляя нагружение в горизонтальной плоскости фрагмента рельса с помощью специального винтового нагружа- теля, закрепленного на стенде, и регистрируя перемещения с помощью прогибомеров. В проведенных экспериментах была произведена оценка зависимости угла поворота рельса в горизонтальной плоскости относи­тельно шпалы от прикладываемого момента [50].

Автором проводились опыты на специальном стенде, с фрагментом рельса типа Р65 длиной 1 м, фрагментом железобетонной шпалы и про­межуточными рельсовыми скреплениями типов КБ-65, ЖБР-65 и АРС-4. Осью поворота условно принималась точка пересечения продольной оси рельса и оси шпалы. Схема испытательного стенда представлена на рис. 8.

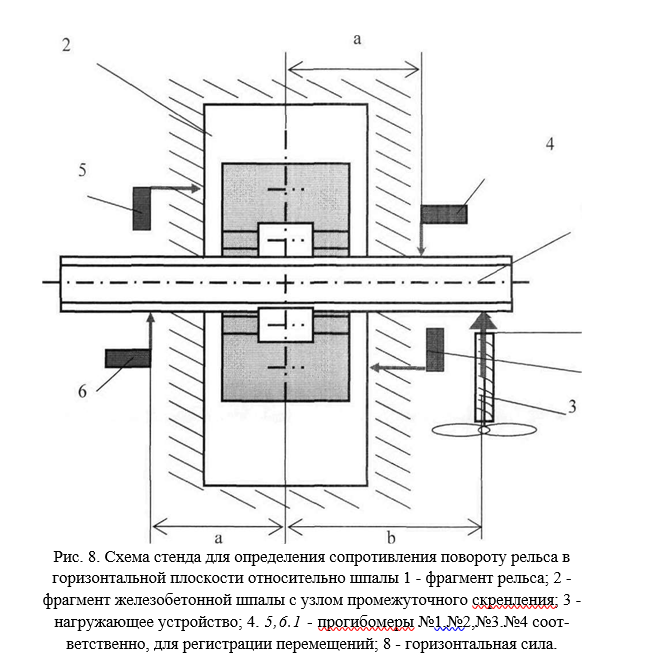
Гайки клеммных болтов затягивались крутящими моментами 50, 100, 150 и 200 Нм, для скрепления типа АРС-4 испытания проводились при 1, 2, 3 и 4 позициях монорегулятора. На стенде через тензометрическое силомерное кольцо к фрагменту рельса монотонно передавалось го­
ризонтальное усилие для поворота вручную с помощью винтового нагружателя [49].

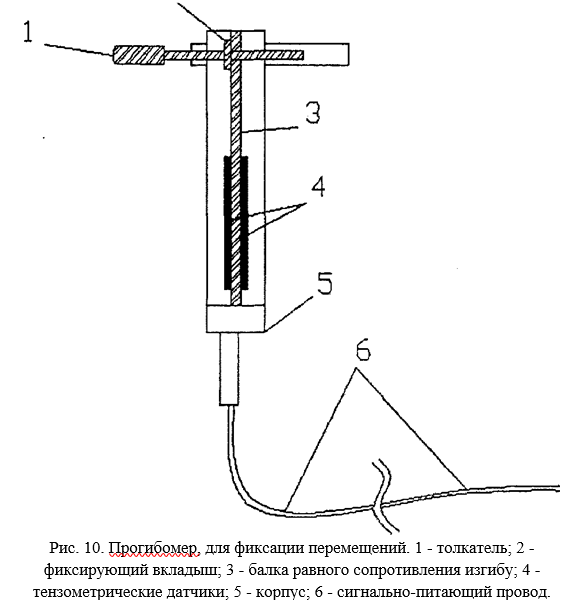
Перемещения фиксировали прогибомерами, показанными на рис. 10.

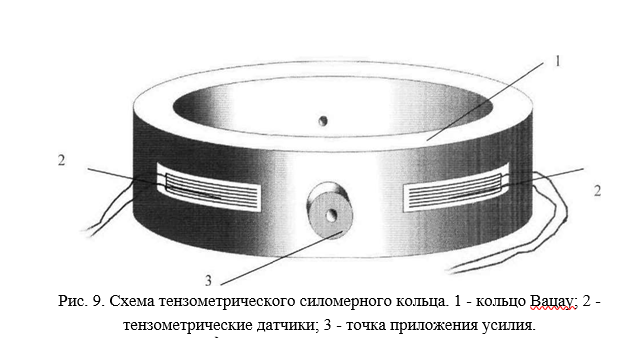
Силу измеряли специальным тензометрическим кольцом, которое устанавливается между винтовым нагружателем 3 и фрагментом рельса 1. Тензометрическое кольцо выполнено из кольца Вацау (динамометр) с на­клеенными на него тензометрическими датчиками рис. 9.

В ходе испытаний определялись следующие параметры:

• угол поворота рельса относительно шпалы, рад;
• реактивный момент, возникающий в узле скрепления рельса, кНм. Схема определения угла поворота рельса относительно шпалы по­казана на рис. 11.

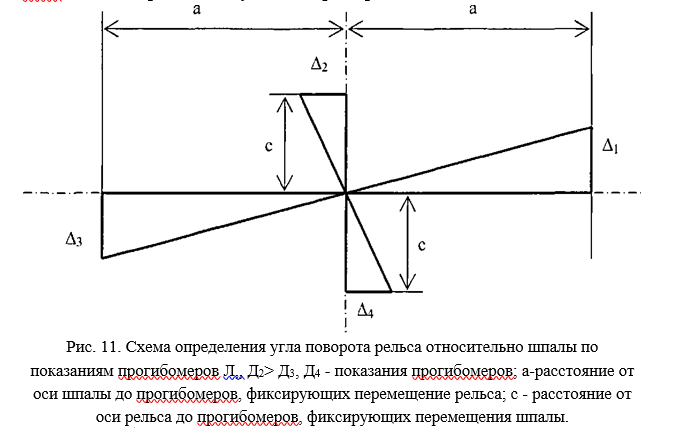
Угол поворота сечения рельса относительно шпалы в горизонталь­ной плоскости ср определялся по формуле

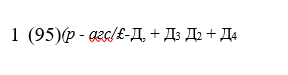
где А] – показание прогибомера № 1; Д₂ – показание прогибомера №2; А₃ – показание прогибомера №3; Д4 – показание прогибомера №4; (р – угол поворота рельса относительно шпалы. Реактивный момент М_Р принимался равным поворотному моменту М_п, который в свою очередь определяется по формуле

где Ь – расстояние от точки приложения горизонтального усилия до оси фрагмента шпалы, м;

<2 – горизонтальное усилие, кН. Горизонтальное усилие фиксируется тензометрическим силомерным кольцом.

Перед началом испытаний проводили тарировку тензометрического силомерного кольца. На кольцо с помощью пресса прикладывали ступе­нями нагрузку от 0 до 10 кН через 1кН, и фиксировали соответствующие им показания тензометрических датчиков, тарировку сохраняли в уста­новках программной среды Са1тап 4.5. Прогибомеры тарировали с помо­щью специальной тарировочной пластины.

Закладные болты подкладочного варианта скреплений должны быть затянуты с крутящим моментом соответствующему нормативному значе­нию для данного типа промежуточного рельсового скрепления.

С помощью винтового нагружателя создавали горизонтальное уси­лие, прикладываемое к фрагменту рельса, причем нагрузку прикладывали монотонно увеличивая. Одновременно с началом приложения нагрузки начинали производить запись показаний тензометрического силомерного кольца и перемещений, регистрируемых прогибомерами.

В ходе испытаний, после каждого поворота рельса относительно шпалы в горизонтальной плоскости и записи, соответствующих ему пока­заний силы и перемещений, ослабляли прижатие рельса к подрельсовому основанию и устанавливали фрагмент рельса перпендикулярно фрагменту шпалы.

Опыты проводятся в объеме 10 циклов для каждого узла промежу­точного рельсового скрепления и определенного усилия прижатия рельса к подрельсовому основанию.

По полученным показателям строят зависимости реактивного мо­мента от угла поворота рельса рис. 7, 8, 9. Затем результаты лабораторных испытаний аппроксимируют трех- параметрической функцией вида:

где R – сопротивление повороту рельса относительно шпал в го­ризонтальной плоскости;

q, М, г – коэффициенты, получаемые при аппроксимации экспери­ментальных данных.

Аппроксимацию выполняли с помощью программы аппроксимации

функции вида R = q-<p+M-arcig— методом наименьших квадратов, напи-

г санной автором на языке программирования Delphi (приложение 2), ин­терфейс которой представлен на рис.12. Для этого необходимо данные по­лученных углов поворота и реактивных моментов сохранить в файлах Ex­cel.

Программа написана таким образом, что исходные данные для ап­проксимации должны сохраняться в файлах Excel, как показано на рис. 13.

После сохранения полученных экспериментальных данных запус­кают программу по аппроксимации этих данных рис. 12. В программе по аппроксимации с помощью функции «настройка» выбирают диапазон и шаг коэффициентов аппроксимации, причем чем меньше будет шаг и больше диапазон, тем точнее рассчитаются коэффициенты.

Полученные экспериментальные значения углов поворота сечения рельса относительно шпалы д> и соответствующие им поворотные момен­ты Л_э, прикладываемые к элементу рельса в испытательной установке приведены на графике (рис. 14)

На рис. 15 приведены результаты аппроксимации сопротивления по­вороту рельса относительно шпал в горизонтальной плоскости для скреп­ления ЖБР-65.

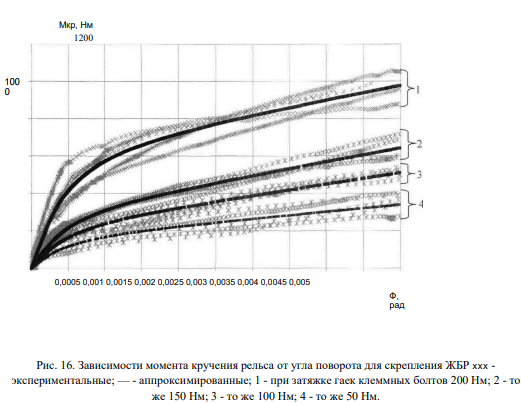
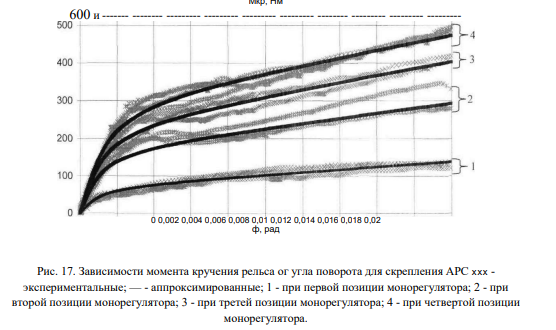
Полученные, в результате аппроксимации значения коэффициентов q, M, г приведены в табл. 5. Коэффициенты аппроксимации q, M, г для скреплений КБ, ЖБР, АРС

Тип скреп­ления	Момент затяж­ки клеммных болтов, Нм (по­зиция моноре­гулятора АРС)	Коэффициенты, характеризующие прижатие скреплений
		г	Эпюра шпал, шт/км
			2000		1840		1600
			M	q	M	q	M	q
КБ-65	50	0,0003	0,4	16	0,368	14,72	0,32	12,8
	100	0,0007	0,64	20,2	0,5888	18,584	0,512	16,16
	150	0,0011	0,88	23,8	0,8096	21,896	0,704	19,04
	200	0,0016	1,22	27,8	1,1224	25,576	0,976	22,24
ЖБР-65	50	0,0004	0,22	70	0,2024	64,4	0,176	56
	100	0,0004	0,3	114	0,276	104,88	0,24	91,2
	150	0,0004	0,4	137	0,368	126,04	0,32	109,6
	200	0,0004	0,84	140	0,7728	128,8	0,672	112
АРС-4	1	0,0009	0,09	7	0,0828	6,44	0,072	5,6
	2	0,0009	0,22	12,5	0,2024	11,5	0,176	10
	3	0,001	0,3	17,5	0,276	16,1	0,24	14
	4	0,0011	0,38	18,5	0,3496	17,02	0,304	14,8

При аппроксимации зависимости Л = следует учитывать важ­нейшее свойство функции ]{(<р) – ее нечетность, т.е. кососимметричность, в силу которой К{-ф) – -Я{<р). Аппроксимация по формуле (97) таким свой­ством обладает. Аппроксимация проводилась методом наименьших квад­ратов.

где Ф{(p-,M,q,r) – функция, зависящая от коэффициентов аппроксима­ции M,q,r при каждом значении q>\

R₃ – сопротивление повороту рельса относительно шпал в горизон­тальной плоскости, полученное экспериментальным путем.

При достижении минимума функции (98), получаем оптимальные значения коэффициентов M,q,r. Для решения данной задачи автором, на языке программирования Delphi, была составлена программа по расчету коэффициентов аппроксимации трехпараметрической функции арктанген­са. С помощью этой программы были найдены коэффициенты M,q,r.