Оценка устойчивости бесстыкового пути в зависимости от вида и условий эксплуатации промежуточных рельсовых скреплений методом дифференциальных уравнений равновесия

Цикл статей:
Глава 1 – Зависимость устойчивости бесстыкового пути от типов промежуточных рельсовых скреплений и условий их эксплуатации

Глава 2 – Экспериментальное определение сопротивления промежуточ­ных скреплений повороту рельсов относительно шпал

Глава 3 – Оценка устойчивости бесстыкового пути в зависимости от вида и условий эксплуатации промежуточных рельсовых скреплений методом дифференциальных уравнений равновесия

Глава 4 – Определение критических параметров оценки устойчивости бесстыкового пути

Существующие методы расчета устойчивости бесстыкового пути пре­дусматривают учет сопротивления повороту рельсов относительно шпал от угла поворота рельса. Однако функция, описывающая сопротивление повороту рельсов относительно шпал, учитываемая в чистом виде, в зави­симости от различных свойств и конструкций промежуточных рельсовых скреплений, может существенно меняться. Далее представлен, разрабо­танный А.Я. Коганом совместно с автором, метод оценки устойчивости бесстыкового пути под действием температурных сил с одновременным определением неблагоприятного сопротивления повороту рельсов относи­тельно шпал в зависимости от угла поворота рельса.

Уравнение сжато-изогнутой рельсовой нити в прямом участке пути имеет вид [7]

где: $у=у(х) – поперечный сдвиг рельсовой плети; EI – изгибная жесткость рельса; f\(y) ~ функция, описывающая сопротивление поперечному пере­мещению рельсовой нити в зависимости от величины перемещения; /₂‘(у’) – функция, описывающая сопротивление повороту рельсов от­носительно шпал в зависимости от угла поворота рельса; Р – продольная сила в рельсе; .Уо =;Уо(*) ” ордината начальной ненапряженной неровности рельсовой нити.

Функцию, описывающую сопротивление рельсовой нити поперечным деформациям можно представить в виде двухпараметрической обратной функцией тангенса, параметры которой, могут быть определены по ап­проксимации экспериментальных данных [27]:

где В, Ь – коэффициенты характеризующие тип балласта, и степень уплотнения. В диссертационной работе Грищенко В.А. на соискание уче­ной степени доктора технических наук был проведен комплекс экспери­ментов по выявлению этих коэффициентов для различных типов балласта и степени его уплотнения. Функцию, описывающей сопротивление повороту рельсов относи­тельно шпал в зависимости от угла поворота рельса, представим в виде трехпараметрической обратной функцией тангенса, параметры которой, могут быть определены также по аппроксимации экспериментальных дан­ных [44]

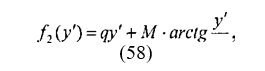
где <7, М, г – коэффициенты, характеризующие тип промежуточного рельсового скрепления и степень прижатия скреплением рельса к подрель- совому основанию. Коэффициенты ц, М, г получают в результате ап­проксимации экспериментальных данных. Методика эксперимента и оп­ределение коэффициентов приведены в следующей главе.

Тогда:

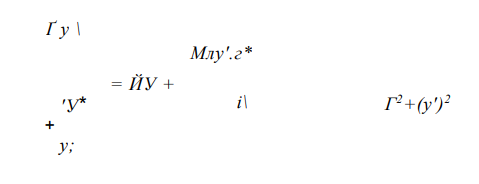
В процессе искривления рельсовой нити в горизонтальной плоскости происходит разрядка продольных сил, поэтому

где Р, – продольная сила, обусловленная изменением температуры рельсов относительно температуры закрепления плетей и принимаемая в дальнейшем за постоянную величину;

Г – продольная сила разрядки в плети при ее искривлении в го­ризонтальной плоскости.

Сила разрядки ) – удовлетворяет интегрально-дифференциальному уравнению [7]

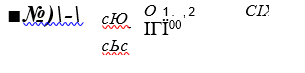
где – погонное сопротивление продольному перемещению сече­ния рельса, зависящее от величины этого перемещения Г – площадь поперечного сечения рельса.

При малых продольных перемещениях функцию /з(С) можно считать линейной

ІЖ) = к £

где к – характеристика погонного сопротивления рельса,

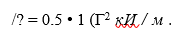
В этом случае уравнение разрядки продольных сил после дифферен­цирования примет вид

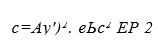
С учетом ограниченности функции О(х) на интервале -со<х<сс реше­ние полученного уравнения может быть записано с использованием функ­ции Грина в следующем виде [15]:

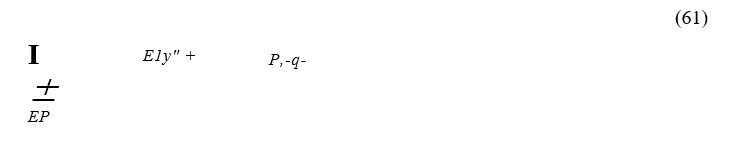
С учетом выражений (57), (59), (60) и (61) уравнение (56) примет вид

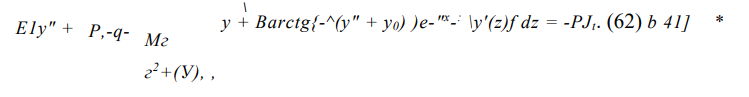
Уравнение (62) описывает продольно-поперечный изгиб рельсовой нити под действием продольной температурной силы Р,. Для исследования устойчивости решения уравнения (62) дадим координате у малое возмущение д, в результате чего система будет совершать возмущенное движение, определяемое также уравнением (62) [46], [47]. На вариацию 3(х) наложим условие, при котором она обращалась бы в нуль в нулях функции у(х). Это требование соответствует наличию в сис­теме равноудаленных друг от друга виртуальных шарниров, определяю­щих начальные условия для кривой изгиба. При соблюдении этого усло­вия функции /, (у + 8) и /₂(/ + 8′;у” + 8″) можно разложить в ряды Тейлора и, учитывая малость д, оставить два первых члена разложения

Функциями, удовлетворяющими уравнению (62) при соответствую­щем выборе формы начальной ненапряженной неровности уо(х) и описы­вающими низшую форму потери устойчивости, являются соответственно

Величины Си»в выражениях (69), (70) и (71) имеют конкретные значения и определяются условием достижения продольной температур­ной силой Р, критического значения Р_1к.

Докажем высказанное положение и вычислим при этом значения кри­тических параметров Р,_к, С и oj, зависящих от размеров начальной нена­пряженной неровности уо(х). Представим начальную ненапряженную неровность у₀(х) в виде

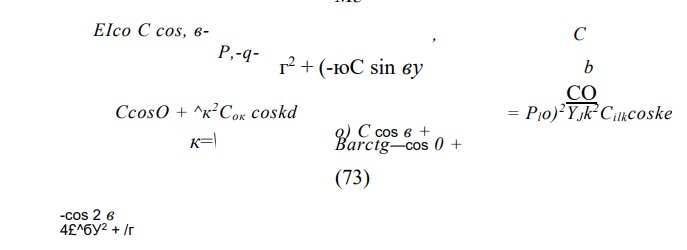
Учитывая, что сила разрядки С(х) определяется нелинейным членом и на порядок меньше продольной температурной силы Р,, в последнем члене левой части полученного равенства можно пренебречь влиянием гармоник разложения (72), так как их учет дает уточнение второго порядка малости. Таким образом, окончательно получим следующее уравнение, связываю­щее параметры напряженной и ненапряженной неровностей:

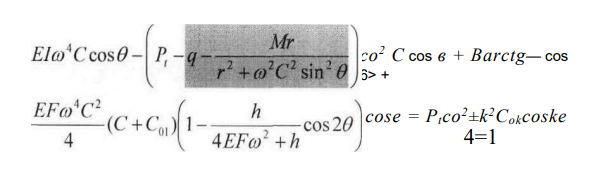
Теперь разложим четные нелинейные функции Barctg—COS,в и

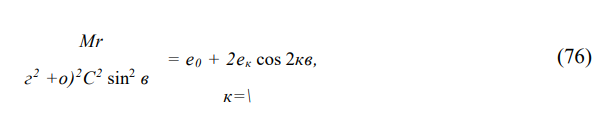
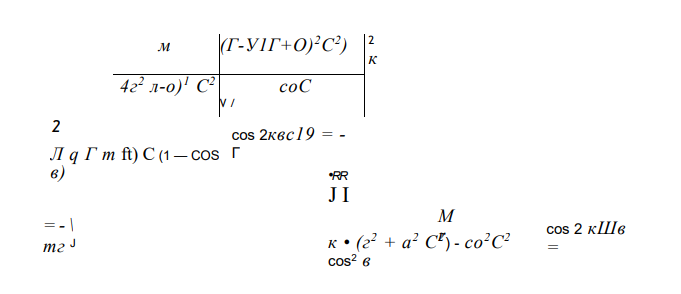
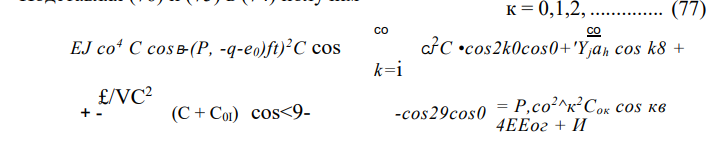
Приравнивая коэффициенты при соб^, получим следующее уравне­ние, связывающее параметры неровностей для низшей формы изгиба

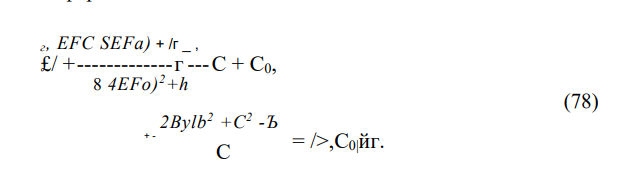
Точно так же, подставляя (76) и (75) в (74) и приравнивая коэффици­енты при cos кб (к=2,3,…), можно получить выражения для величин С₀к:

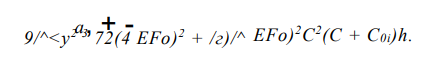
Последний член в выражении для С₀з обусловлен учетом разрядки продольных сил в рельсовых плетях.

Таким образом, при начальной ненапряженной неровности, имеющей вид разложения (71) с коэффициентами С₀к,определяемыми условиями (78) и (79), решение (69) удовлетворяет нелинейному интегрально- дифференциальному уравнению (62).

Практически коэффициенты С_ок (к = 2,3,…) весьма малы, так что с достаточной точностью начальную ненапряженную неровность для рас­сматриваемого неблагоприятного расчетного случая можно считать коси- нусоидной у₀ (х) = С₀ COS (ОХ .

Здесь и далее для упрощения записи принято Сщ = Со.

Вернемся к рассмотрению уравнения в вариациях (68), определяюще­го устойчивость решения (69).

Разложим нелинейные функции в уравнении (68) в ряд Фурье. Ис­пользуя (69) и учитывая, что функции цг{у),4(у’) четные и имеют период л, получим

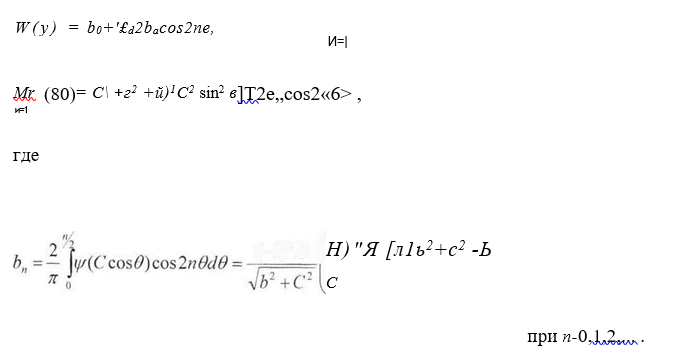
Коэффициенты по прежнему определяются формулой (76)

Подставляя (69), (71), (79) и (80) в (68) и пренебрегая влиянием гар­моник в члене, учитывающем разрядку продольных сил, порождающих величины второго порядка малости, получим

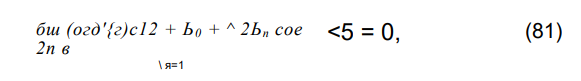
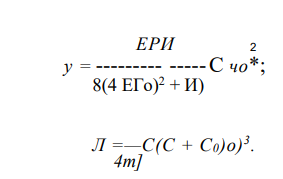
Решение уравнения (80) с учетом требования обращения его в нуль в нулях функции у(х) будем искать в виде

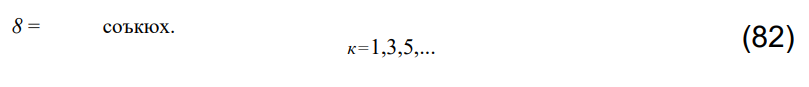
Подставляя (82) в уравнение (81), произведя умножение тригономет­рических функций и интегрирование и приравнивая коэффициенты при одинаковых соъкюх, получим бесконечную систему нелинейных однород­ных уравнений относительно Ск- Группируя члены, запишем эти уравне­ния так:

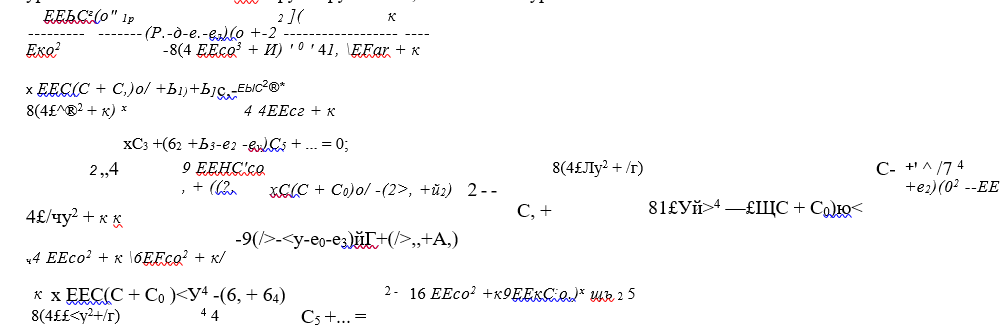
Элементы трех центральных диагоналей определителя, стоящего в ле­вой части уравнения (84), имеют вид

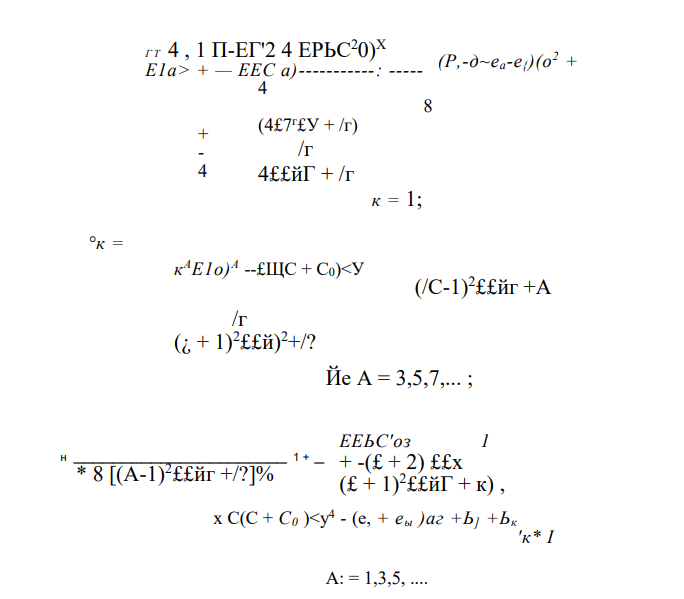
Уравнение (84) по внешнему виду схоже с уравнением критических частот для уравнения Матье – Хилла [48] и решается методом последова­тельных приближений. В первом приближении можно пренебречь влияни­ем гармоник и удержать в определителе диагональные члены. Таким обра­зом, в первом приближении соотношение критических параметров можно определить из выражений

Для низшей формы изгиба (к=1) уравнение (86) принимает вид

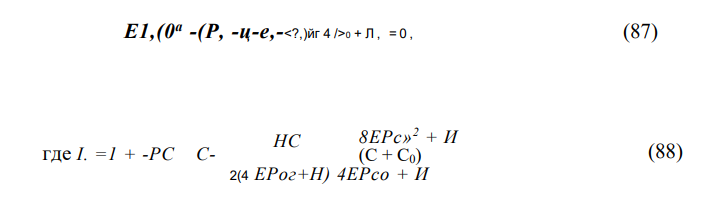
Величину /у можно назвать приведенным моментом инерции рельса, учитывающим разрядку продольных сил в нем.

Поскольку находится периодическое решение (71), величина со в уравнении (87) должна быть действительной и положительной при мини­мальном значении продольной температурной силы Р_т. Это требование приводит к выражениям

Уравнения (89), (90) и (78) совместно с выражением (88) определяют при заданной амплитуде начальной ненапряженной неровности Со=Со/ длину неровности Ь=2ж/со, амплитуду напряженной неровности С и кри­тическую температурную силу Р,*.

Для решения системы (91) может быть использован метод итераций, основанный на том, что второе слагаемое в выражении для приведен­ного момента инерции (88) на порядок меньше первого.

Для кривого участка пути при перемещении рельсовой нити во внеш­нюю сторону кривой, в ней возникают относительные продольные удлине­ния.

На практике невозможно разделить ненапряженную и напряженную (силовую) неровности. В эксплуатации, возможно замерить только их сум­му, бытовую неровность С_б = С₀ + С. Система трансцендентных уравнений для кривого участка будет вы­глядеть так

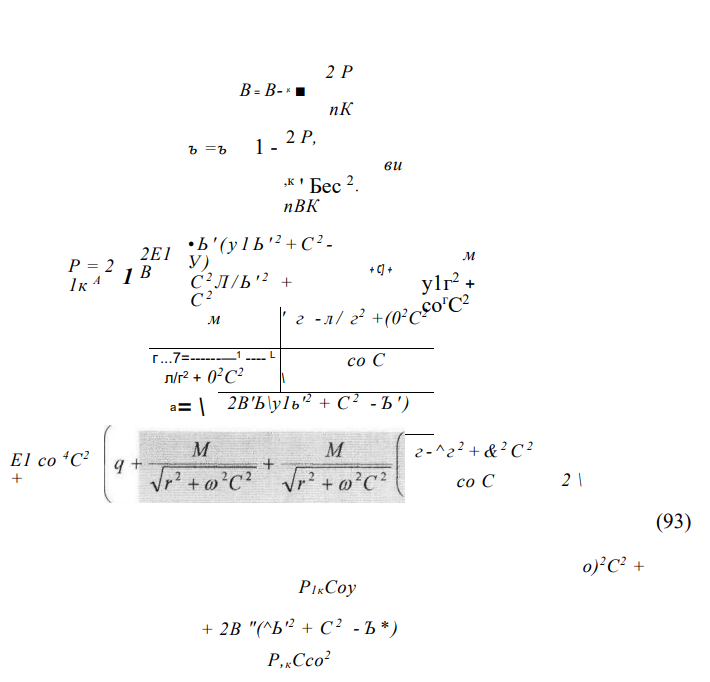
При проведении расчетов по формулам (93) следует проверять соблю­дение условия

При несоблюдении условия (94) полностью исчерпывается несущая способность пути в поперечном горизонтальном направлении, и рельсы на­чинают интенсивно перемещаться в наружную сторону кривой (без выбро­са).

Значения коэффициентов М, ц и г, входящих в систему уравнений (93), определяются аппроксимацией экспериментальных данных, зависят от конструкции промежуточных рельсовых скреплений и степени прижатия рельса к подрельсовому основанию.

Алгоритм решения системы (93) строится следующим образом. Зада­ются в первом приближении значением критической продольной силы, на­пример Р_1к = 2 -10³ кН, и решают первые три уравнения системы (93), при раз­
личных значениях переменной С. Во втором приближении расчет ведут с уче­том полученного в первом приближении значения критической продольной силы Р_1к. Для получения практически точного результата достаточно про­ведения трех итераций для каждого значения аргумента С.