Цикл статей:
Глава 1 – Методы и алгоритмы диагностики неисправностей стрелок с электродвигателями переменного токаГлава 2 – Анализ неисправностей стрелок с электродвигателями переменного тока
Разработка методов логического анализа функции мощности перевода стрелок с электродвигателями переменного тока
Использование нейронной сети, обученной на выборке, содержащей примеры всех рассмотренных неисправностей, не позволяет произвести полное диагностирование стрелок с электродвигателями переменного тока, т.к. наблюдается большой процент ошибочного классифицирования. Причиной этому является то, что классы, описывающие неисправности Н3-Н7 [Приложение Г], расположены в пересекающихся областях пространства диагностических критериев, что затрудняет их разделение. Для снижения процента ошибок распознавания разработаны методы логического анализа функции мощности перевода для определения неисправностей Н3, Н4, Н6, Н7.


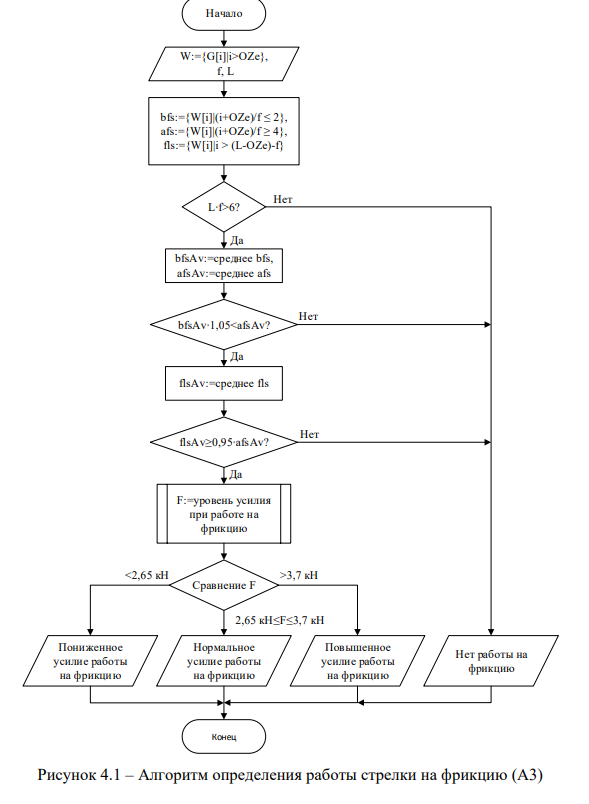
Для определения наличия и степени проявления неисправности «Не параллельное прилегание остряка к рамному рельсу» используется алгоритм А4 (рисунок 4.2).
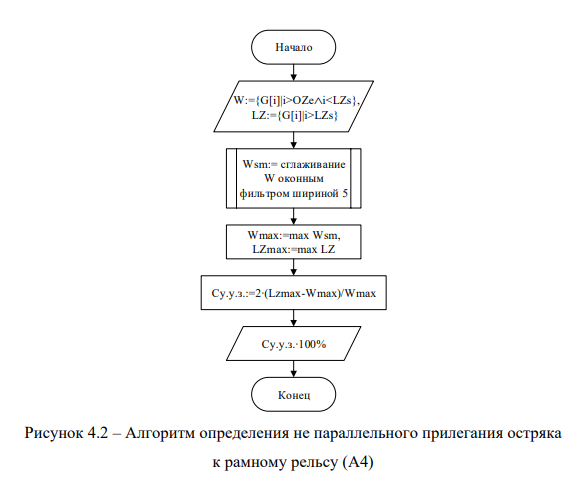
Исходным данными являются множество точек графика мощности в рабочей зоне W и множество точек графика мощности в зоне запирания LZ. Производится сглаживание W с помощью оконного фильтра [65] с окном шириной 5 по формуле (4.3). Применение оконного фильтра позволяет исключить влияние случайных резких пиков графика мощности в рабочей зоне на работу алгоритма.

Разработка алгоритмов выделения зон режимов работы стрелочного электропривода на графиках мощности перевода
Различные неисправности стрелочных переводных устройств с электродвигателями переменного тока отличаются не только по месту неисправности (электропривод, гарнитура, цепи питания) в устройстве, но и по месту проявления неисправности на графике мощности перевода. Так, наличие переходного сопротивления на фазах питания ЭД проявляется в начальной области графика перевода, наличие пружинности стрелочных остряков — ближе к центральной части графика, не параллельное прилегание остряка к рамному рельсу можно выявить в конечной области, а остальные неисправности проявляются на всей длительности работы шибера. Поэтому актуальной является задача выявления на графике мощности перевода областей, позволяющих рассчитать ДК и диагностировать неисправности.
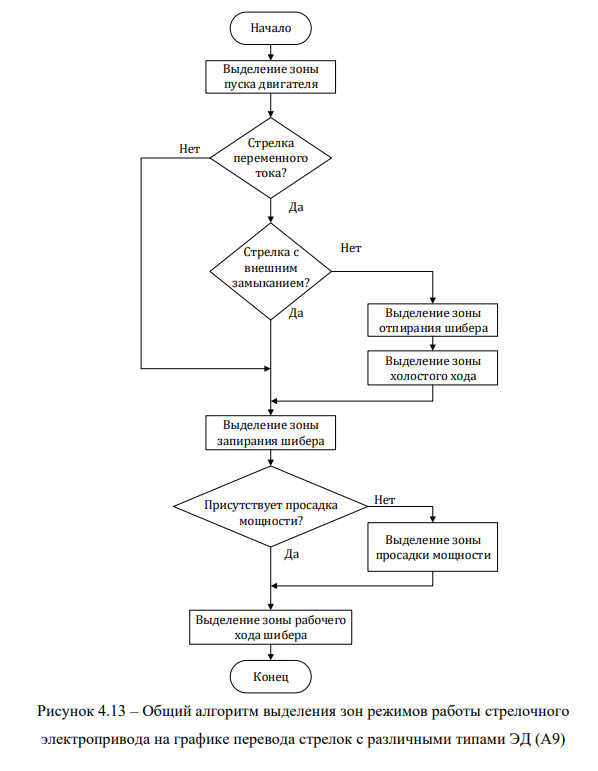
У графиков мощности перевода стрелок с ЭД переменного тока можно выделить следующие области графика перевода, характерные для различных режимов работы стрелочного электропривода (рисунок 4.3):
- Зона пуска двигателя.
- Зона холостого хода.
- Зона отпирания шибера.
- Зона просадки мощности (при наличии пружинности стрелочных остряков).
- Зона работы шибера (рабочая зона).
- Зона запирания шибера.
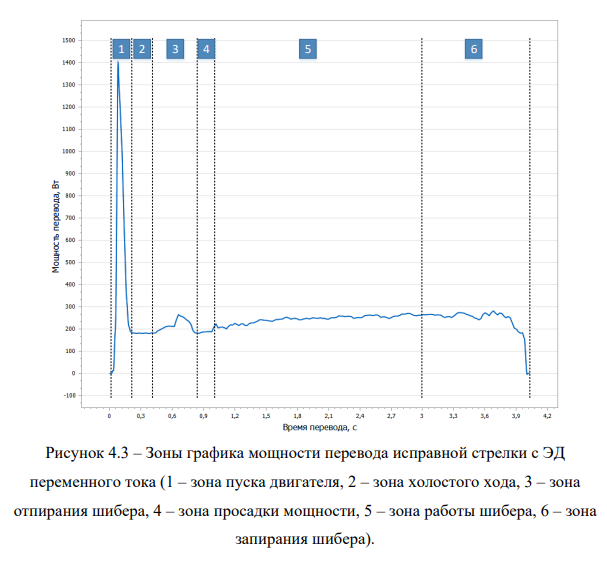
Зона пуска двигателя определяется границами стартового пика перевода или совокупности пиков, объединенных в один стартовый пик. При поиске этой зоны на графике перевода следует помнить о возможности ситуации, когда на одном графике перевода приводится перевод двух спаренных стрелок, или, когда происходит работа стрелки на фрикцию, и на схемах управления имеется функция автовозврата стрелок в исходное положение при длительной работе на фрикцию (рисунок 4.4).
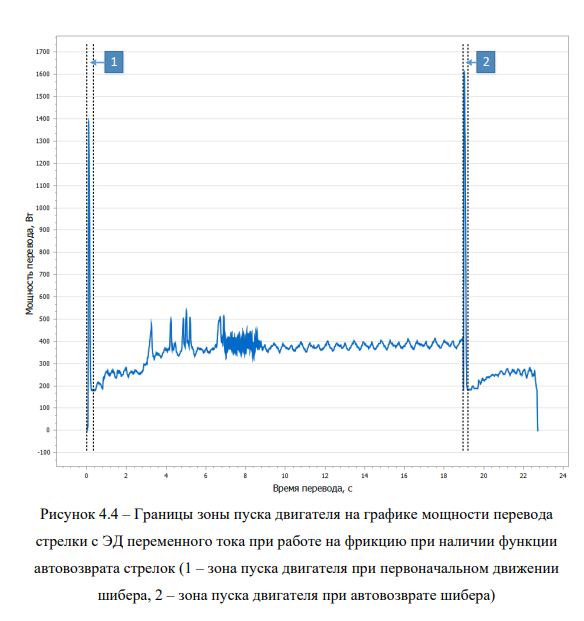
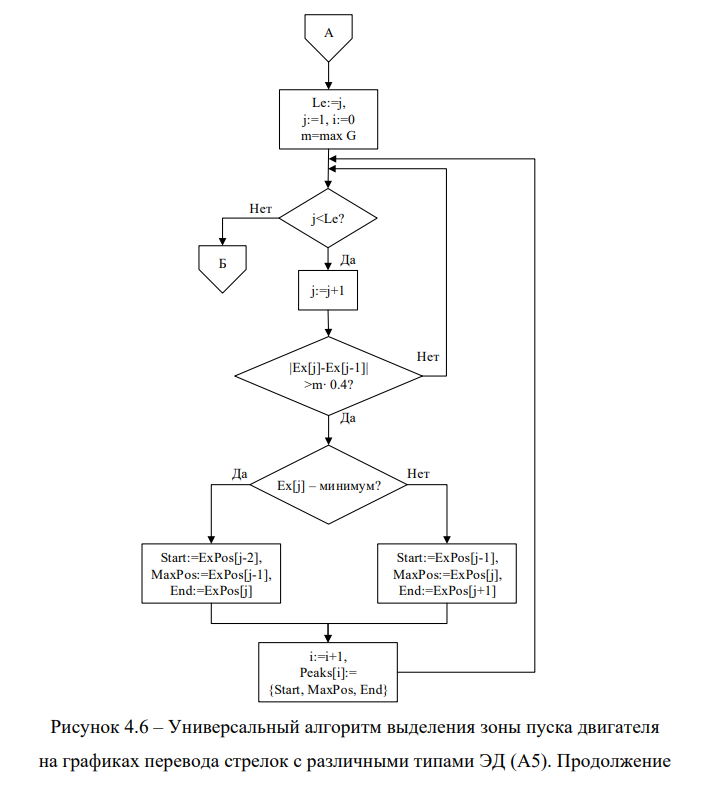
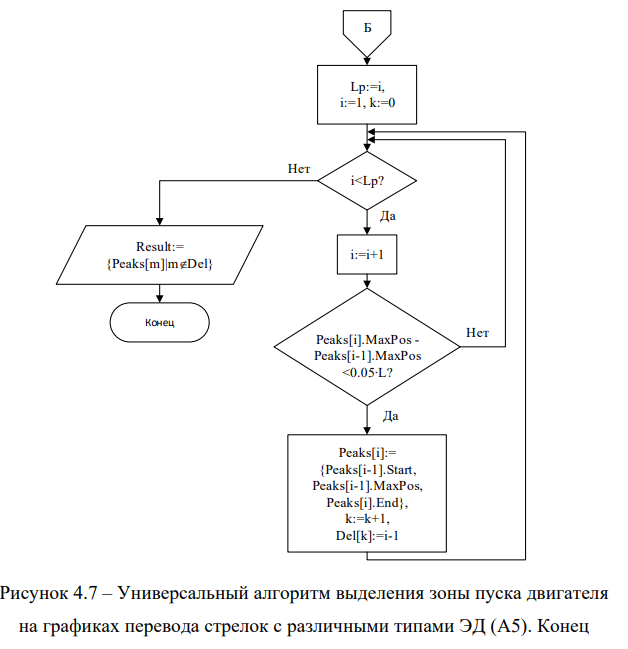
С учётом вышеизложенных возможных ситуаций разработан универсальный алгоритм выделения зоны пуска двигателя на графиках перевода стрелок с различными типами ЭД (А5) (рисунки 4.5-4.7).
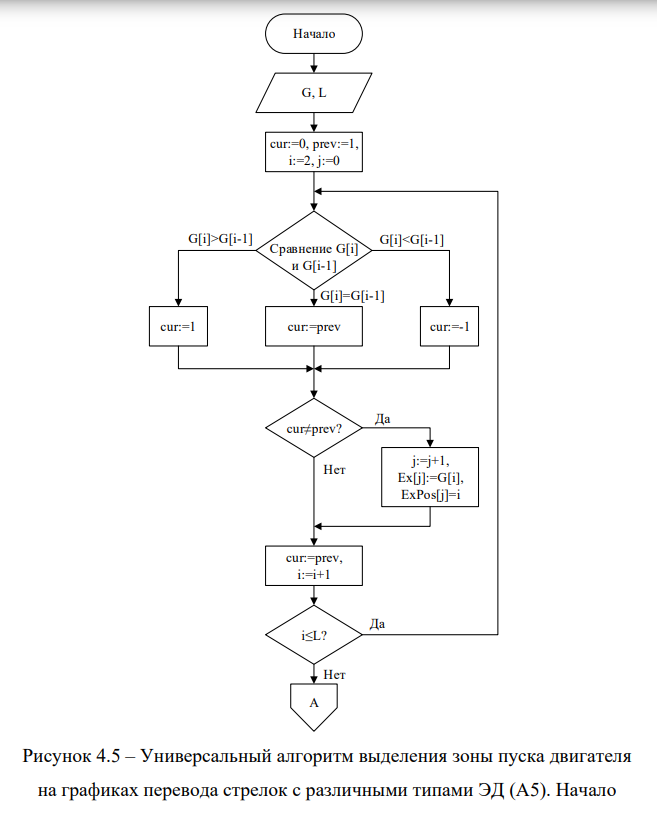
На вход алгоритма подаётся вектор всех точек графика перевода G размерностью L. Объявляются переменные prev и cur, описывающие соответственное предыдущее и текущее направление изменения графика. При этом «1» означает рост графика на отрезке, а «-1» — падение графика. Переменной prev присваивается значение «1», так как очевидно, что любой график будет начинаться с роста значений.
Далее в цикле сравниваются G[i] — значение текущего элемента вектора G — со значением предыдущего элемента G[i-1]. Если текущий элемент больше предыдущего, значит, график имеет тенденцию к росту, и переменной cur присваивается «1 ». Если текущий элемент меньше предыдущего, значит,
наблюдается падение графика, и переменной cur присваивается «-1». При равенстве значений считается, что график продолжает изменяться в том же направлении, поэтому cur получает то же значение, что есть у prev. Затем происходит сравнение направлений изменения графика. Если они не равны, значит G[i] — экстремум графика. Таким образом, происходит наполнение массива Ex значениями экстремумов графика G и наполнение массива ExPos индексами положения экстремумов в векторе G. Затем в prev записывается текущее направление изменений, и алгоритм переходит на следующий шаг цикла.
Объявляется переменная m для хранения максимального значения точек вектора G, и ей присваивается значение. Объявляется переменная Le — размер массивов Ex и ExPos. Далее в цикле проверяются все найденные экстремумы. Находится разница между текущим и предыдущим значением вектора Ex по модулю, и сравнивается с величиной 40% от m. Это позволяет выделить самые большие перепады значений на графике. Если полученная величина больше необходимого уровня, то это свидетельствует о наличии пика рядом с этим экстремумом. Вычисляются индексы начала, конца и индекс максимального значения пика в зависимости от того, является ли экстремум минимумом или максимумом. Полученные индексы полностью описывают пик, который добавляется в список всех пиков перевода Peaks.
После этого в цикле проверяются все элементы вектора Peaks размерностью Lp. Сравниваются индексы максимальных значений двух соседних пиков. Если разница между индексами меньше, чем 5% длительности перевода — пики считаются соседними и объединяются в один, с индексом старта первого пика и индексом конца второго пика. Информация о новых границах объединенного пика записывается вместо текущего пика, а индекс предыдущего пика сохраняется в массив Del индексов, которые предстоит удалить из вектора Peaks. Полученный в итоге вектор пиков Result является списком всех зон пуска двигателя, найденных на графике. Зная зоны пуска двигателя, можно разделить график с несколькими последовательными переводами на одиночные переводы, и выделить следующие зоны режимов работы стрелочного электропривода.
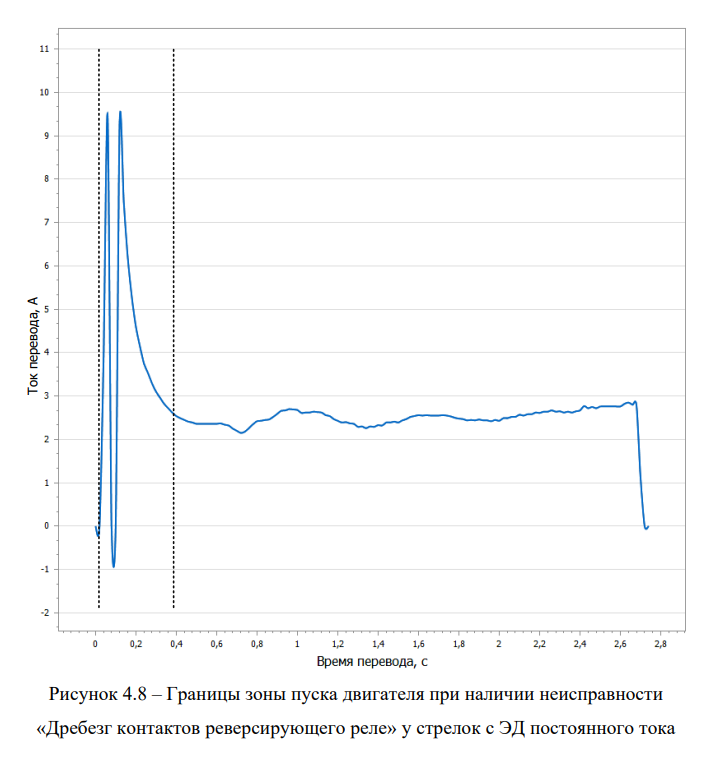
Алгоритм является универсальным, т.к. его можно использовать в задаче диагностики стрелок с ЭД постоянного тока. Алгоритм учитывает ситуации, при которых возникает необходимость в объединении нескольких пиков в один стартовый пик, например, при наличии неисправности «Дребезг контактов реверсирующего реле» стрелок с ЭД постоянного тока (рисунок 4.8).
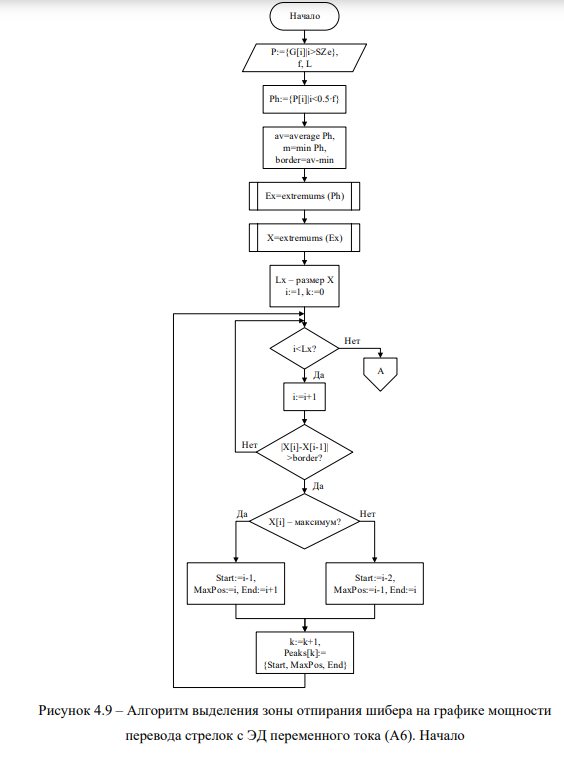
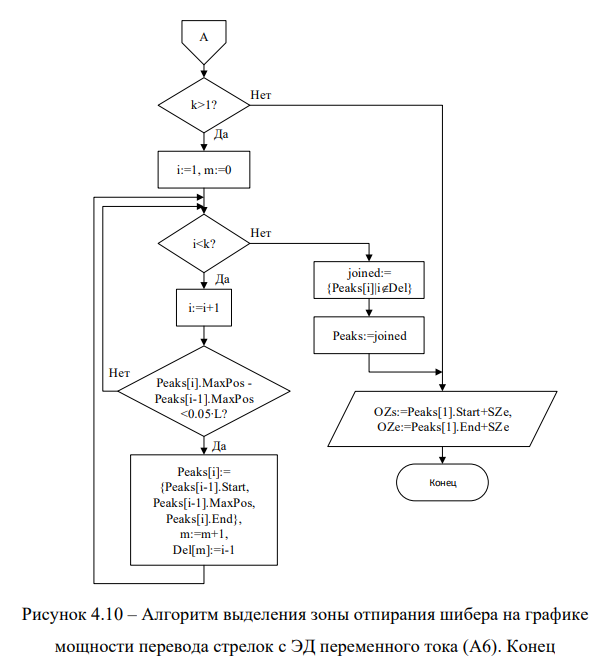
Следующей зоной, которую необходимо определить для выделения остальных зон, является зона отпирания шибера. Наличие этой зоны характерно для всех графиков мощности перевода стрелок с ЭД переменного тока, кроме стрелок с внешним замыканием. Алгоритм выделения зоны отпирания шибера (А6) представлен на рисунках 4.9-4.10.
На вход алгоритма подаётся вектор P всех точек графика мощности одиночного перевода за исключением зоны пуска двигателя, индекс конца зоны пуска двигателя SZe, частота дискретизации измерений f и число точек на графике мощности перевода L (количество элементов вектора G). Из этого вектора в вектор Ph выделяются точки, описывающие первые полсекунды перевода после конца зоны пуска двигателя — предполагаемую область холостого хода. По точкам вектора Ph рассчитывается значение переменной border, которая понадобится для поиска сильного изменения на графике.
Затем аналогично подобной операции в алгоритме выделения зоны пуска двигателя, из вектора Ph выделяются экстремумы, которые заполняют вектор Ex. Затем в вектор X заносят экстремумы вектора Ex. Это позволяет отфильтровать небольшие изменения на графике и анализировать только ключевые точки перегиба.
Далее в цикле сравнивается разница между текущим и предыдущим элементом вектора X. Если эта разница больше величины border, это является признаком наличия выпуклости на графике. Вычисляются индексы начала, максимальной точки и конца области выпуклости графика, в зависимости от того, является ли текущее значение X[i] максимумом или минимумом графика мощности перевода. Полученные значения заносятся в массив Peaks.
Затем в цикле элементы массива Peaks проверяются на близкое расположение максимальных точек. Аналогично подобной операции в алгоритме выделения зоны пуска двигателя, близкие элементы объединяются в один, лишние элементы удаляются. Вычисляются индекс OZs начала зоны отпирания шибера и индекс OZe конца зоны отпирания шибера.


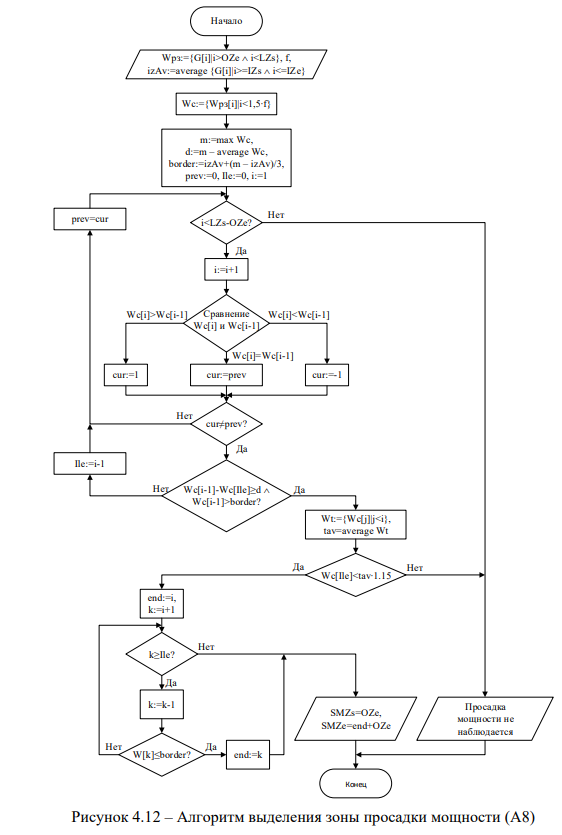
Для выделения зоны просадки мощности на вход алгоритма подается вектор Wp3, который содержит точки вектора G от OZe — индекса конца зоны отпирания, до LZs — индекса начала зоны запирания шибера. Также подается величина izAv, описывающая среднее значение мощности перевода в зоне холостого хода двигателя. Из вектора Wрз выделяют вектор Wc, который содержит точки Wрз от 0 до индекса, описывающего 1,5 с перевода. Производится расчет величины d, описывающей требуемую разницу между значениями вектора Wc в текущей точке цикла и в месте последнего экстремума Ile, и величины border, описывающей граничный уровень мощности, после которого проявляется рост мощности после просадки. Затем в цикле выделяются экстремумы графика, и каждый последующий экстремум сравнивается с предыдущим. Если разница между экстремумами больше d и значение мощности в этой точке больше border, это является признаком, что наблюдается наличие просадки мощности. Затем в цикле от к до Ile выполняется поиск элемент массива Wc, чьё значение меньше border. Индекс этого элемента описывает начало роста мощности после просадки. Индексом начала зоны просадки мощности принимается индекс конца зоны отпирания шибера.
Таким образом, для выделения всех зон режимов работы стрелочного электропривода на графике мощности перевода стрелки следует использовать алгоритм А9 (рисунок 4.13). Информация о границах всех зон, полученная с помощью этого алгоритма, позволяет рассчитать диагностические критерии и произвести диагностику стрелок с ЭД переменного тока. Алгоритм А9 можно использовать в задаче диагностики неисправностей стрелок с ЭД постоянного тока (например, для определения границ, необходимых для расчёта ДКП в [34]). Но в отличие от графиков мощности перевода стрелок с ЭД переменного тока, на графиках тока перевода стрелок с ЭД постоянного тока можно визуально выделить только зоны пуска двигателя, рабочую зону и зону запирания шибера.
Интегрированный метод определения неисправностей стрелок с ЭД переменного тока. Обработка результатов классификации
В результате сбора базы примеров неисправностей было определено, что 65% графиков переводов, записываемых СТДМ, имеют некорректную форму. Это связано с местом установки датчиков СТДМ, контролирующих ток и напряжение перевода. Контроллеры подключаются в общую цепь питания стрелочных электроприводов, поэтому при одновременном переводе происходит наложение графиков друг на друга, что делает невозможным анализ одиночных переводов (рисунок 4.14). Поэтому возникает необходимость фильтрации графиков по их типу. На рисунке 4.15 представлен алгоритм определения типа графика (А10).

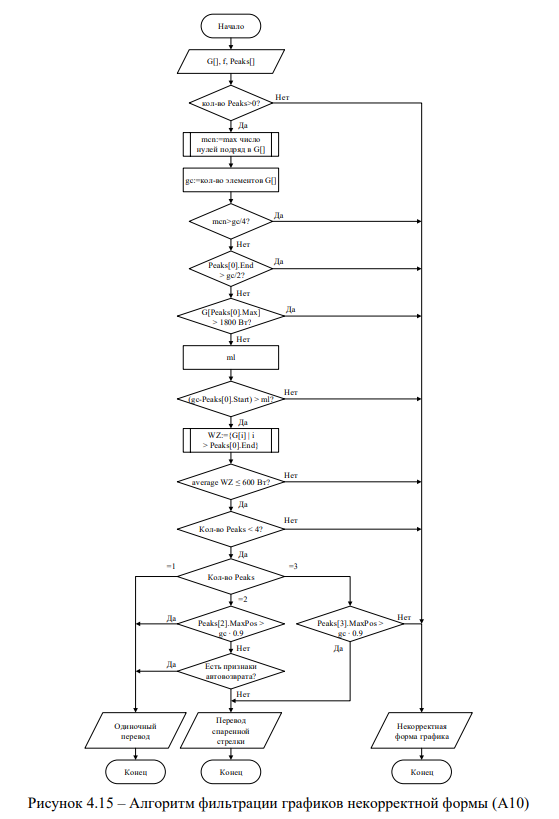
Входными данными для алгоритма являются массив измерений мощности перевода G, частота измерений f и список пиков графика Peaks. Отсутствие пиков на графике перевода (количество элементов списка Peaks равно 0), определенных алгоритмом определения зон пуска (алгоритм А5), является первым признаком некорректной формы графика.
Оценивается количество mcn идущих подряд нулевых элементов массива G. Определяется gc — длина массива G. Если максимальное число подряд идущих нулевых элементов больше, чем четверть длины массива мощности перевода, то график имеет некорректную форму. Также график имеет некорректную форму, если конец стартового пика находится позже середины графика перевода, или если пусковая мощность превышает 1800 Вт.
Устанавливается минимальная допустимая длительность перевода в секундах ml. Для графиков мощности перевода стрелок с ЭД переменного тока ml=3 сек, для постоянного тока ml=1.5 сек.
Выделяется массив WZ, который состоит из элементов массива G, расположенных после стартового пика, и описывает предполагаемую рабочую зону перевода. Среднее значение элементов этого массива должно быть меньше 600 Вт.
Затем анализируется количество элементов массива Peaks. Если число элементов равно 1 — значит график имеет корректную форму и описывает одиночный перевод стрелки. Если количество пиков равно 2, и отсутствуют признаки увеличенной мощности в конце перевода или наличия функции автовозврата стрелки при работе на фрикцию, то график имеет корректную форму и описывает перевод спаренных стрелок. Если указанные признаки присутствуют на графике мощности перевода, значит график имеет корректную форму и описывает одиночный перевод стрелки. Если количество пиков равно 3 и присутствует признак наличия увеличенной мощности в конце перевода, значит график имеет корректную форму и описывает перевод спаренных стрелок. Иначе алгоритм определяет некорректную форму графика.
Для повышения качества классификации технических состояний было решено применять интегрированный метод определения неисправностей. Результаты работы нейронной сети и методов логического анализа объединяются в один массив результатов R, при этом первые 4 элемента массива соответствуют выходам нейронной сети, а остальным выходам присваивается значение, характеризующее степень проявления неисправностей, определяемых с помощью методов логического анализа. Интегрированный алгоритм А11 приведен на рисунках 4.16-4.17:
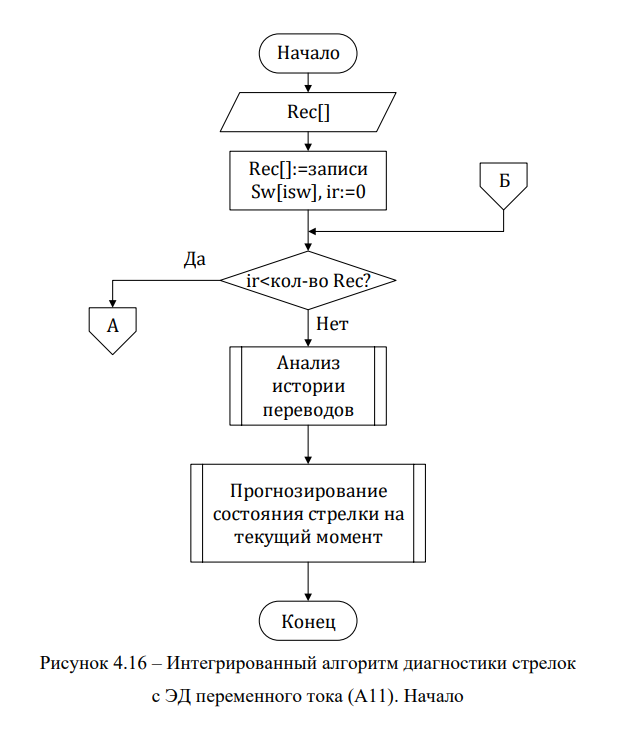
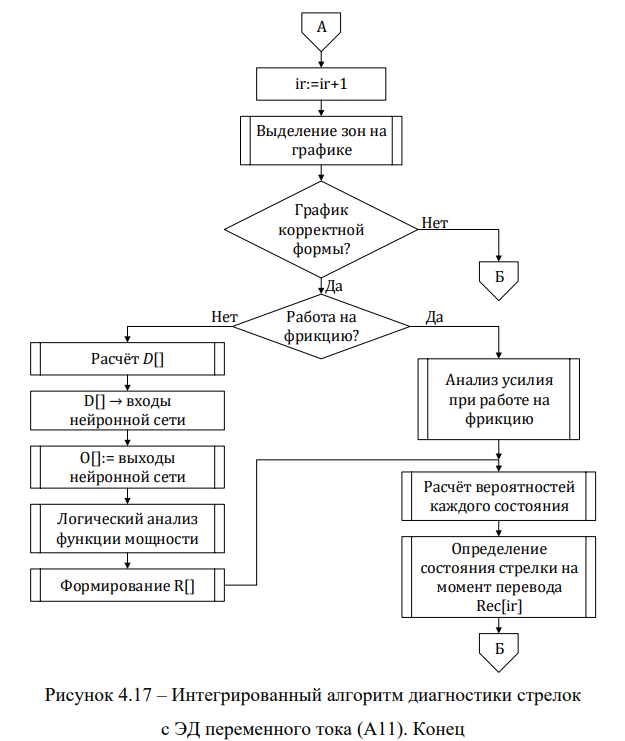
В цикле анализируется техническое состояние каждого перевода Rec из архива переводов стрелки, хранимого в СТДМ. По алгоритму А9 выделяются зоны графика перевода стрелки, затем с помощь алгоритма фильтрации (алгоритм А10) отсеиваются графики некорректной формы. Если форма графика перевода соответствует графику работы стрелки на фрикцию, анализируется уровень усилия перевода при работе на фрикцию, чтобы определить наличие или отсутствие разрегулировки фрикционного сцепления (неисправности Н3, Н4).
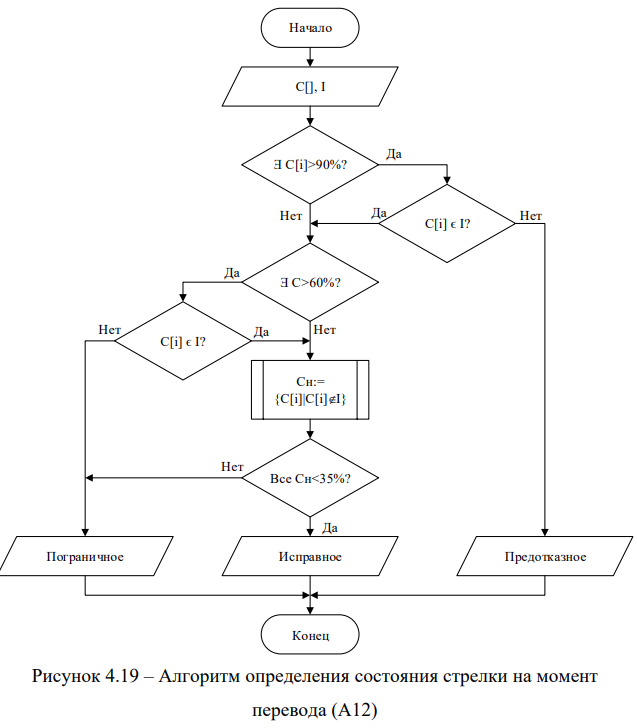
Если отсутствуют признаки работы стрелки на фрикцию, производится вычисление диагностических критериев и формирование массива входов нейронной сети. В результате вычислений, производимых нейронной сетью, появляется массив выходов, описывающий степень проявления неисправностей Н1, Н2, Н5. Затем определяется степень проявления неисправностей Н6 и Н7. Формируется единый массив результатов R и рассчитывается вероятность каждого из состояний, и затем оценивается состояние стрелки на момент перевода. Затем с помощью линейной регрессии по последним пяти переводам прогнозируется техническое состояние стрелки на текущий момент.
Предложена следующая диаграмма технических состояний (рисунок 4.18), основанная на диаграмме возможных состояний систем ЖАТ [66].
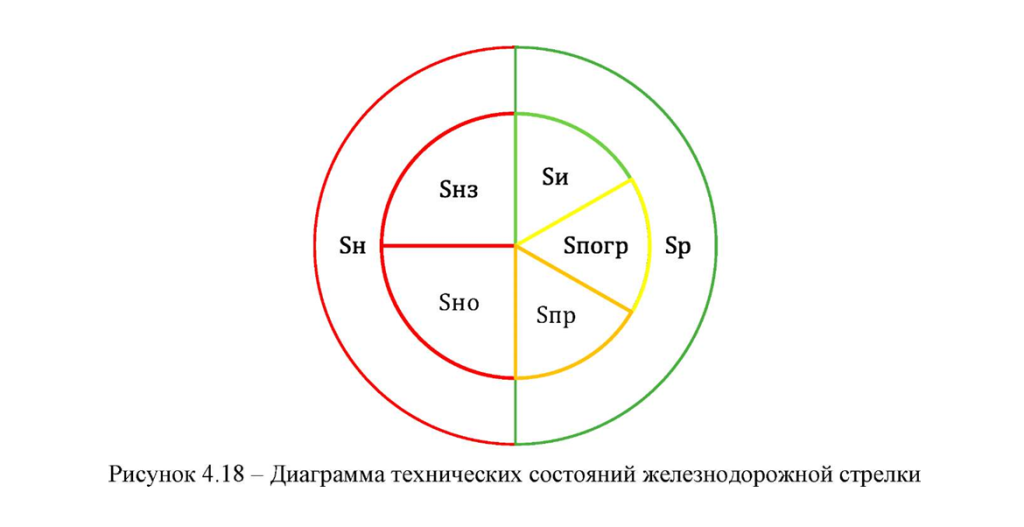


Определение состояния стрелки на момент перевода позволяет проанализировать историю переводов и определить необходимость срочного ремонта стрелки.
Выводы
В [34] приведены диагностические критерии для модели диагностики СПУ с ЭД постоянного тока, но не были разработаны методы выделения зон режимов работы электропривода на графике функции тока, необходимых для расчёта этих критериев. Для возможности расчёта диагностических критериев и работы методов логического анализа функции мощности перевода стрелок с ЭД переменного тока разработаны алгоритмы и методы выделения зон режимов работы электропривода на графике функции мощности перевода.
- Для расчёта ДК de разработан универсальный алгоритм выделения зоны пуска двигателя на графиках перевода стрелок с различными типами ЭД (алгоритм А5).
- Разработан алгоритм выделения зоны отпирания шибера на графике мощности перевода стрелок с ЭД переменного тока (алгоритм А6), обеспечивающий выделение рабочей зоны рабочего хода шибера.
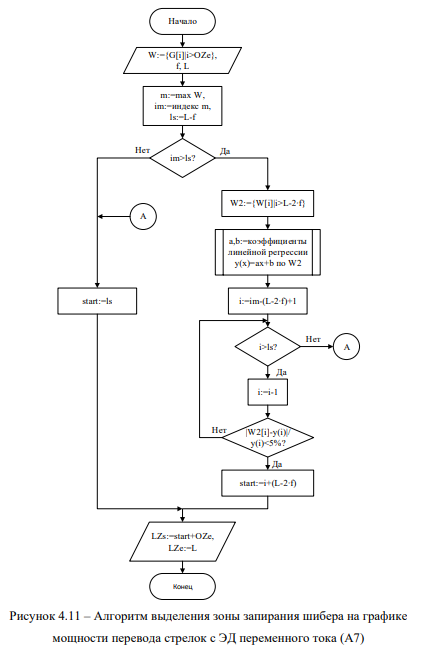
- Разработан алгоритм выделения зоны запирания шибера на графике мощности перевода стрелок с ЭД переменного тока (алгоритм А7), позволяющий рассчитать ДК d9 и позволяющий выделить зону рабочего хода шибера.
- Разработан алгоритм выделения зоны просадки мощности (алгоритм А8), необходимый для определения неисправности Н6.
- Рабочая зона перевода определяется по границам зоны отпирания шибера, зоны просадки мощности и зоны запирания шибера. Информация о границах рабочей зоны позволяет рассчитать ДК di-d5, di, ds, dio.
- Разработан общий алгоритм выделения зон режимов работы стрелочного электропривода на графике перевода стрелок с ЭД как переменного тока, так и постоянного тока (алгоритм А9).
- Для снижения процента ошибок распознавания разработаны методы логического анализа функции мощности перевода стрелок с электродвигателями переменного тока, применяемые для определения неисправностей Н3 (алгоритм А3), Н4 (алгоритм А3), Н6 (формула 4.2) и Н7 (алгоритм А4).
- Исследование архивов переводов стрелок из СТДМ показало, что примерно 65% графиков имеют некорректную форму по причине того, что контроллеры подключаются в общую цепь питания стрелочных электроприводов, и при одновременном переводе нескольких стрелок на станции происходит наложение графиков одиночных переводов друг на друга. Для решения этой проблемы разработан алгоритм фильтрации графиков некорректной формы (А10).
- Для объединения результатов работы нейросетевой модели диагностирования и метода логического анализа функции мощности перевода синтезирован интегрированный алгоритм диагностики стрелок с ЭД переменного тока (А11).
- Разработан алгоритм оценки состояния стрелки на момент перевода (А12): исправного, пограничного и предотказного. Введенная градация состояния позволяет различать исправные стрелки; стрелки, ремонт которых необходимо запланировать; и стрелки, требующие немедленного ремонта.
Список литературы
- Lu D. A survey of image classification methods and techniques for improving classification performance [Текст] / D. Lu, Q. Weng //International journal of Remote sensing. — 2007. — Т. 28. — №. 5. — С. 823-870.
- Garrett D. Comparison of linear, nonlinear, and feature selection methods for EEG signal classification [Текст] / D. Garrett et al. // IEEE Transactions on neural systems and rehabilitation engineering. — 2003. — Т. 11. — №. 2. — С. 141-144.
- Лаптин Ю. П. О некоторых подходах к проблеме построения линейных классификаторов в случае многих классов [Текст] / Ю. П. Лаптин, А. П. Виноградов, А. П. Лиховид // Pattern Recognition and Image Analysis. — 2010. — Т. 20. — №. 2. — 21 с.
- Дмитриев Е. А. Метод опорных векторов [Текст] / Е. А. Дмитриев // Научные исследования и разработки студентов. — 2017. — С. 131-132.
- Hearst M. A. Support vector machines [Текст] / M. A. Hearst et al. // IEEE Intelligent Systems and their applications. — 1998. — Т. 13. — №. 4. — С. 18-28.
- Ben-Bassat M. Sensitivity analysis in Bayesian classification models: Multiplicative deviations [Текст] / M. Ben-Bassat, K. L. Klove, M. H. Weil // IEEE Transactions on Pattern Analysis and Machine Intelligence. — 1980. — №. 3. — С. 261-266.
- Журавлев Ю. И. Построение нелинейных классификаторов в случае многих классов [Текст] / Ю. И. Журавлев, Ю. П. Лаптин, А. П. Виноградов // Applicable Information models. ITHEA, Sofia. — 2011. — С. 7-13.
- Хайкин С. Нейронные сети [Текст]: полный курс, 2-е издание. — Издательский дом Вильямс. — 2008.
- Зуев. Д. В. Синтез объектной нейросетевой модели распознавания образов и ее применение в задачах железнодорожной автоматики [Текст]: дис. … канд. техн. наук: 05.13.18 / Д. В. Зуев. — СПб.: Санкт-Петербург. гос. ун-т путей сообщения. — 2013.
- Благовещенская Е. А. Приложения сверточных нейронных сетей к задачам распознавания схем железнодорожной автоматики. Особенности применения [Текст] / Е. А. Благовещенская и др. // Международная конференция по мягким вычислениям и измерениям. — Федеральное государственное автономное образовательное учреждение высшего образования Санкт-Петербургский государственный электротехнический университет ЛЭТИ им. ВИ Ульянова (Ленина). — 2017. — Т. 1. — С. 471-473.
- Генрихов И. Е. Классификация на основе полных решающих деревьев [Текст] / И. Е. Генрихов, Е. В. Дюкова // Ж. вычисл. матем. и матем. физ., 52:4. – 2012 — С. 750-761
- Степанов Р. Г. Технология Data Mining: интеллектуальный анализ данных [Текст] / Р. Г. Степанов // Казань: КГУ. — 2008.
- Болодурина И. П. Построение дерева решений при решении задачи классификации факторов, влияющих на востребованность учебной литературы [Текст] / И. П. Болодурина, П. А. Болдырев, С.Т. Дусакаева. // Тр. междунар. конф. «Перспективные инновации в науке, образовании, производстве и транспорте. — С. 85-89.
- Андреев И. М. Описание алгоритма CART [Текст] / И. М. Андреев // Exponenta Pro: Математика в приложениях. — 2004. — №. 3-4. — С. 48-53.