Цикл статей:
Глава 1 – Зависимость устойчивости бесстыкового пути от типов промежуточных рельсовых скреплений и условий их эксплуатацииГлава 4 – Определение критических параметров оценки устойчивости бесстыкового пути
Введение
Актуальность темы. Одним из основных направлений повышения надежности и эффективности железнодорожного пути является расширение сферы применения бесстыкового пути.
В годы строительства в России железных дорог, в частности дороги Санкт-Петербург — Москва, в путь укладывались очень короткие рельсы (длиной 3,675; 4,572 и 5,486 м). При столь коротких рельсах на каждом километре железнодорожного пути возникало от 360 до 540 рельсовых стыков [1]. В конструкцию пути тогда входили весьма легкие рельсы, (масса 26,3 кг/м), слабые стыковые соединения и песчаный балласт. При такой конструкции большая часть затрат труда и средств путейцев уходили на поддержание в исправном состоянии рельсовых стыков, смену рельсов из-за их изломов в тех же рельсовых стыках, выправку пути в плане и профиле, на устранение угона пути и т.д. В результате угона пути многие рельсовые стыки оказывались предельно растянутыми или сжатыми. Так, например, на перегоне Торбино — Боровинка Николаевской дороги летом 1866 г. около 200 рельсов оказались настолько плотно сжатыми в стыках, что, не имея возможности свободного температурного удлинения при их естественном нагреве, стали коробиться кверху, искривились вбок в сторону путевой канавы и опустились на поверхность балласта; так произошел один из первых «выбросов пути» на железных дорогах России [2]. В те же годы при низких температурах в зимнее время наблюдались многочисленные случаи разрыва рельсовых стыков и даже рельсов на тех участках, где в результате угона на значительном протяжении пути стыки оказались предельно растянутыми, и растягивающие усилия срезали болты в этих стыках. Все это побуждало путевых работников вводить в практику более длинные рельсы. К началу первой мировой войны в России средняя длина рельсов превышала первоначальную в 2 — 3 раза. И все же, принятая тогда концепция о необходимости уменьшать в рельсах продольные температурные силы за счет зазоров в стыках продолжала господствовать в практике железных дорог России вплоть до 20 — 30-х годов XX века [3]. В 90-е годы прошлого столетия инженеры-путейцы на своих съездах и страницах журналов уже обсуждали проблемы создания бесстыкового пути. Естественно, что первые шаги в решении проблемы бесстыкового пути делались в направлении разработки его конструкций с периодической сезонной разрядкой продольных температурных сил в рельсовых плетях, а также попытки создания конструкции с автоматической саморазрядкой продольных усилий в рельсах. К такого рода предложениям необходимо отнести конструкции пути И.Р. Стецевича (1896 г.), А.И. Ольденборгера (1904 г.), И.А. Бородкина (1938 — 1940 гг.), М.С. Боченкова (1948 г.) [4]. В 50 — 60-е годы XX века многократно возросла грузонапряженность железных дорог России, увеличились нагрузки от подвижного состава на путь, скорости движения поездов. Все это потребовало повсеместного значительного повышения прочности и устойчивости верхнего строения пути за счет применения тяжелых типов рельсов, более совершенных типов рельсовых скреплений, железобетонных шпал, щебеночного балластного слоя, защиты пути от угона и т.п. Но еще ранее, в 20 — 30-е годы, рядом ведущих ученых начали проводиться экспериментальные и теоретические работы по созданию конструкций температурно-напряженного бесстыкового пути (работы Членова М.Г.). Эти исследования позволяли начать разработку конструктивной, технологической и нормативной базы для проектирования и применения таких конструкций на железных дорогах, создать Технические условия их применения в эксплуатации, технологий их укладки, ремонта, текущего содержания и диагностики устойчивости бесстыкового пути.
Естественно, все это потребовало большого объема экспериментальных и теоретических исследований, наблюдений за опытными участками бесстыкового пути различных конструкций при действии в его рельсовых плетях больших продольных сжимающих сил.
Разработкой аналитических методов определения значений предельно допускаемых по устойчивости бесстыкового пути продольных сжимающих температурных сил в рельсовых плетях занимались многие исследователи. Так, в бывшем СССР методы расчета устойчивости бесстыкового пути разрабатывали К.Н. Мищенко [5], С. П. Першин [6], А.Я. Коган [7], С.И. Морозов [8] и др.; во Вьетнаме — Нгуен Ван Туен [9] в Венгрии — И. Немешеди, Э. Немчек [10], в Германии — Г. Майер [11], Ф. Рааб; в Австрии — Э. Энгель [12]; во Франции — А. Мартине [13] и Р. Леви; в Чехословакии — Л. Сакмауэр [14]; в Англии — Д. Бартлет и Д. Туор; в Японии — М. Нумато [15] и др.
В процессе эксплуатации возникают как конструктивные, так и технологические отказы, снижающие эффективность конструкции бесстыкового пути. При этом ряд отказов имеет специфический характер, определяемый особенностями бесстыкового пути и условиями эксплуатации.
Введение в обращение тяжеловесных поездов повышенной массы привело к увеличению сил действующих на путь от подвижного состава. В частности, исследования на Дальне-Восточной железной дороге показали, что продольные силы в пути вызывают увеличение боковой нагрузки в крутых кривых выше 100 кН. Поэтому, возникает необходимость повышения боковой устойчивости пути, особенно в крутых кривых. По мнению автора, этого можно добиться путем дифференциации промежуточных рельсовых скреплений по условиям эксплуатации. Для бесстыкового пути необходима дифференциация промежуточных скреплений в зависимости от плана пути (радиус кривых участков), регионов его укладки и т.п.
Цель настоящей работы — повышение устойчивости бесстыкового пути и расширение сферы его применения за счет дифференциации требований к промежуточным рельсовым скреплениям.
Для достижения данной цели необходимо:
исследование конструктивных и технологических особенностей работы промежуточных рельсовых скреплений;
определение сопротивления повороту рельса относительно шпалы в зависимости от типа скрепления и условия его эксплуатации;
разработка дополнений к техническим требованиям к промежуточным рельсовым скреплениям.
Методика исследования основана на использовании комплекса теоретических и экспериментальных исследований, среди которых:
- методы нелинейной устойчивости бесстыкового пути;
- методы статистической обработки результатов экспериментов;
- экспериментальные исследования по определению сопротивления промежуточного рельсового скрепления повороту рельса относительно шпалы в горизонтальной плоскости.
Научную новизну представляют:
- дополнения и уточнения физико-математической модели расчета устойчивости бесстыкового пути, касающиеся учета типа промежуточного рельсового скрепления и условий его эксплуатации в данной конструкции пути;
- экспериментально определенные коэффициенты, характеризующие сопротивление скрепления повороту рельса относительно шпалы в горизонтальной плоскости;
- методика и программа расчета устойчивости бесстыкового пути с определением численных значений, написанная на языке программирования Delphi, разработанная на основе методов исследования нелинейной устойчивости упругих систем.
Практическая ценность диссертации:
- установлено влияние типа промежуточного рельсового скрепления и условий его эксплуатации (прижатие рельса к подрельсовому основанию) на устойчивость бесстыкового пути;
- на основе разработанной методики получены рекомендации уточняющие значений допускаемых повышений температур рельсовой плети по условию устойчивости в зависимости от типа скреплений;
- дифференцированная таблица повышений температур рельсовых плетей допускаемых по условию устойчивости пути против выброса для типов скреплений КБ-65, ЖБР-65, АРС-4 (рекомендации к Техническим указаниям по устройству, укладке, содержанию и ремонту бесстыкового пути, табл. П.2.1., Допускаемые повышения температур рельсовых плетей).
На защиту выносятся:
- дополненная и уточненная физико-математическая модель расчета устойчивости бесстыкового пути, позволяющая оценить промежуточные рельсовые скрепления и условия их эксплуатации в данной конструкции пути;
- программа расчета устойчивости бесстыкового пути с определением критических параметров, написанная на языке программирования Delphi;
- предложения по изменению технических требований к промежуточным рельсовым скреплениям ЦП 1 -86;
- предпосылки для разработки рекомендаций к техническим указаниям по устройству, укладке, содержанию и ремонту бесстыкового пути.
Результаты работы и ее отдельные предложения докладывались на конференции «Развитие железнодорожного транспорта в условиях реформирования» на экспериментальном кольце ВНИИЖТ в г. Щербинка в 2006 г. и на конференции «Организация перевозок опасных грузов наземным транспортом» Московская обл., п. Ильинское ОЦ «Ласточка».
Анализ основных методов определения устойчивости бесстыкового пути
Первые методы оценки устойчивости пути появились еще в 19 веке. По существу они отражали лишь какой-то определенный этап работы конструкции, который был исследован разработчиками опытным путем. После появления бесстыкового пути со сварными стыками возникла необходимость разработки теории, которая бы реально отражала его состояние в процессе эксплуатации.
Начало теоретических исследований устойчивости бесстыкового пути относится к 1913 г [16]. За последующие годы были созданы разные варианты методов расчета величин продольных критических сил в рельсах: энергетический, интегральных уравнений, дифференциальных уравнений и др. Значительный вклад в решение этих вопросов внесли российские ученые: В.Г. Альбрехт, М.С. Боченков, Е.М. Бромберг, М.Ф. Вериго, Н.П. Виногоров, В.А. Грищенко, Н.Б. Зверев, Э.П. Исаенко, Н.И. Карпущенко, С.И. Клинов, А.Я. Коган, A.A. Кривобородов, B.C. Лысюк, К.Н. Мищенко, С.И. Морозов, В.И. Новакович, С.П. Першин и другие, а так же зарубежные ученые: О. Амман, М. Балух, К. Грюневальдт, Д. Игнятич, Г. Майер, Нгуен Ван Туен, И. Немешди-Немшек, Э. Немежди, М. Нумата, Р. Леви, и другие. В каждом из предложенных методов сделаны упрощающие расчетную схему допущения, приняты различные формы деформаций рельсов в плане до выброса, имеются различия в исходных уравнениях равновесия и в величинах задаваемых исходных данных. Выбор метода расчета зависит от многих факторов, главные из которых:
а) необходимая точность расчета — один метод прост для решения, но менее точен, другой метод имеет более высокую степень точности, но требует трудоемких вычислений и большого объема исходных данных;
б) большинство методов позволяют определить только предельные величины, без отслеживания переходных процессов, однако именно переходные процессы при потере устойчивости представляют наибольший интерес, так как именно они дают более глубокое понимание сущности процесса выброса пути.
Энергетический метод расчета устойчивости бесстыкового пути
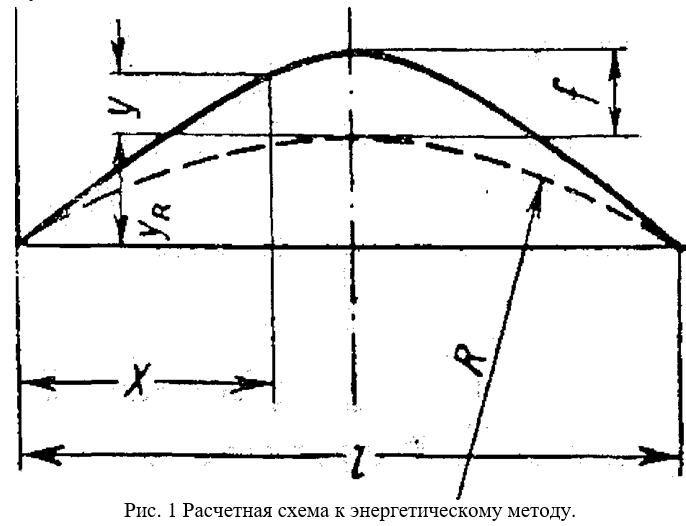
Впервые в законченном виде данный метод был опубликован немецким специалистом К. Грюневальдтом в 1931г. В качестве условия равновесия в этом методе используют либо равенство нулю суммы элементарных работ (обобщенных сил), либо условие экстремума потенциальной энергии системы, из которых находят критическую сжимающую силу. Расчетная схема к энергетическому методу приведена на рис. 1.
Основные допущения, которые применялись при энергетическом методе расчета:
1) Колея условно принимается в виде однородного стержня, с собственным сопротивлением изгибу =£х2У (Е — модуль упругости рельсовой стали, 2.1 — момент инерции двух рельсов относительно вертикальной оси);
2) Силы сопротивления продольным перемещениям и деформациям поворота рельсов считаются равномерно распределенными по длине деформируемого участка пути;
3) В первоначальном состоянии стержень считается прямым или очерченным строго по круговой кривой, то есть начальные неровности не учитываются.
Условие равновесия при энергетическом методе расчета устойчивости пути базируется на принципе возможных перемещений из равенства элементарных работ.
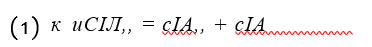
где с1Ак — элементарная работа сжимающих сил на концах искривления; £¿4//- элементарная работа деформации изгиба рельсов; с!АБ— элементарная работа по преодолению сил сопротивления «среды».
Элементарные работы определяются по следующим формулам
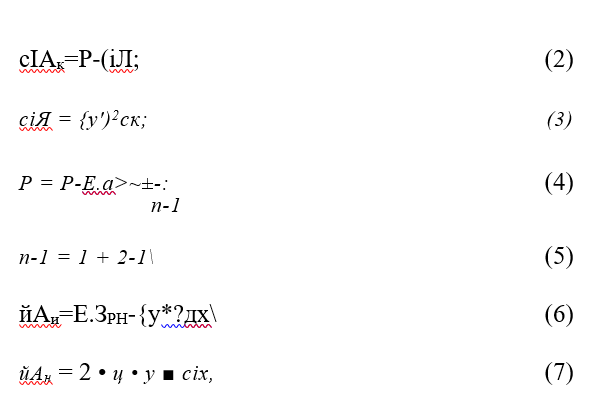
где Р — продольная температурная сила в плети;
^ — продольная сила в плети на концах искривления (с учетом разрядки напряжений за счет удлинения при изгибе);
со — площадь поперечного сечения рельсов;
3РВ— момент инерции 2-х рельсов относительно вертикальной оси;
/- длина хорды изогнутой части плети;
/, — длина изогнутой части плети;
X = (/, — /) — удлинение стержня при деформации;
Ь — длина деформируемых прямолинейных участков стержня;
д — погонное сопротивление поперечному сдвигу;
то — реактивный момент сопротивления одного комплекта скрепления;
е — междушпальное расстояние (по осям шпал); п — безразмерный коэффициент, выражающий отношение полной длины, на которой происходит деформация, к длине искривленной части стержня;
/- стрела изгиба кривой;
г — погонное сопротивление сдвигу рельсошпальной решетки; У =ДХ) ~ уравнение функции изогнутой оси рельса. Полные работы определяются интегрированием элементарных составляющих по следующей формуле
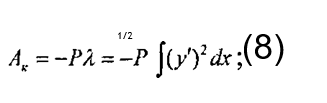
Формой искривления при энергетических методах решения задаются, поэтому функция у=/(х), описывающая упругую линию стержня при изгибе, является заданной.
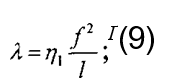
Энергия нагрева расходуется на упругий изгиб стержня и в работу по преодолению сил сопротивления среды.
Работа по преодолению равномерно распределенного по длине стержня сопротивления среды

Как видно из формул, численное решение напрямую зависит от принятого уравнения изогнутой оси пути.
В своей работе, опубликованной в 1932 г.,[16], инж. А. Блох в качестве кривой изгиба принял уравнение (13) рис. 2

Постоянные ц в уравнениях конечных работ имеют вид: г]к =л2/4, т]и =л\ т]и =1/2. Для большей наглядности при решении уравнений А. Блох применял графоаналитические методы. Однако смещенная синусоида не отвечает реальным условиям изгиба в части изменения кривизны. В начале и в конце искривления кривизна скачкообразно изменяется от 0 до некоторого конечного значения, что соответствовало бы заделке концов стержня, которой нет на самом деле. К. Н. Мищенко нашел другие уравнения, которые более полно отвечают реальным условиям искривления оси пути [17]. Так, для случая одностороннего искривления он принял уравнение следующего вида
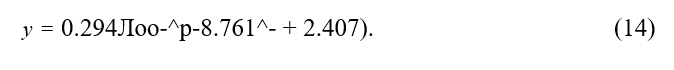
Полученные при этой кривой изгиба, постоянные коэффициенты, имеют следующие значения: 77^ = 2,786, ^,=2,68, ^2=7,18. Решение, полученное К.Н. Мищенко, дало результаты критического усилия на 5% меньше, чем при использовании уравнения смещенной синусоиды.
Для нахождения расчетных уравнений при двустороннем выбросе колеи в горизонтальной плоскости К. Н. Мищенко предложил составную 8 — образную кривую, которая в отличие от использованных ранее кривых не имеет скачков кривизны в начале, конце и точках сопряжения составляющих кривых. Начальный и конечный участок этой кривой на длине — определяются уравнением (14), средний участок на длине — уравнением (15)
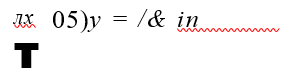
В результате, им были получены следующие значения для коэффициентов: щ =2,416, =5,81, щ =19,18, 7/4 =2,88 .
В дальнейшем, многие исследователи, применявшие для решения задачи определения критической силы в бесстыковом пути энергетический метод, предлагали различные варианты уравнений изогнутой оси. Г. Мей- ер в своей работе, опубликованной в 1937г. предложил следующие уравнения для изогнутой оси пути: для изгиба колеи в одну сторону на кривой, уравнение имеет вид (16)
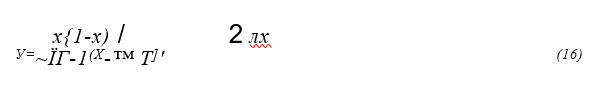
где — радиус кривой изгиба;
для двухстороннего £ — образного изгиба на прямом участке применяется составная кривая, определяемая формулой (17)
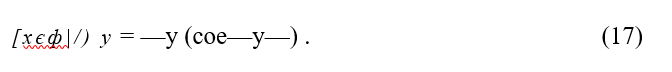
Ординаты кривой (17) являются суммой ординат у, параболы, которой заменяется окружность, радиуса Я ввиду малости центрального угла дуги с хордой /, и ординат у2 смещенной синусоиды. В начале искривле
ния в обоих случаях допускаются скачки кривизны. Скачок в изменении первой и второй производных в составной кривой имеет место и в точках сопряжения смещенной синусоиды с косинусоидой. Таким образом, принятая форма искривления отвечает реальным условиям изгиба лишь в части изменения ординат. Такой же 8-образной кривой пользовался и К. Грю- невальдт.
Японский исследователь Н. Нумата в 1957г получил универсальную формулу, справедливую для всех наблюдавшихся при опытах формах искривления [15]. К рассмотрению принимались следующие кривые, характеризующие форму деформированного пути:
а) при одностороннем искривлении — смещенная синусоида (13);
б) при 8 — образном искривлении — составная кривая (17);
в) при волнообразном искривлении с тремя волнами — составная кривая, определяемая формулой (18):

г) при волнообразном искривлении, составная кривая, вида (19)
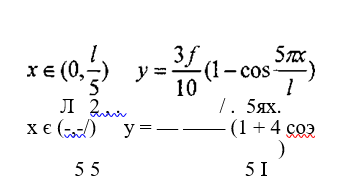
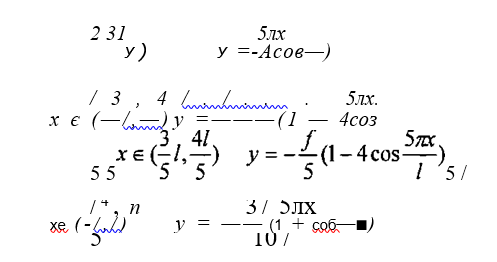
Все составные кривые, принятые в данном решении имеют скачкообразное изменение кривизны в начале, конце искривления и точках сопряжения кривых. Таким образом, в части соответствия принятых уравнений реальной форме искривления это решение имеет существенные недостатки. В случае рассмотрения изгиба колеи на круговой кривой ординаты последней учитываются как ординаты параболы, аналогично методу Г. Мейера, рассмотренному выше. Окончательная формула, связывающая критическую стрелу и критическую силу, имеет вид:
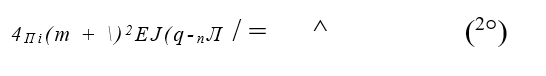
Значения коэффициентов ц5, rj7) rjs, в зависимости от числа волн искривления т приведены в таблице 1.
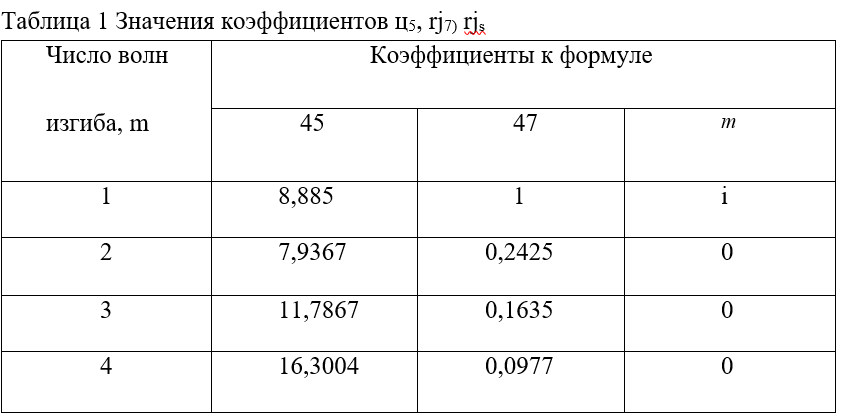
Аналогичное по характеру решение, так же учитывающее различные формы искривления, разработано в 1958г. в Венгрии, доцентом Э. Немеш- ди [18], [19]. Автор применил энергетический принцип при составлении условий равновесия для своих выводов, однако он отказался от общепринятого выражения кривой изгиба через тригонометрические функции, которые заменил на алгебраические многочлены. Коэффициенты для этих многочленов находятся в соответствии с граничными условиями для искривления той или иной формы. Так, для одностороннего искривления на прямой, которое во всех рассмотренных решениях, кроме решения К. Н, Мищенко, выражается смещенной синусоидой, Э. Немешди подобрал уравнение, вида (21)
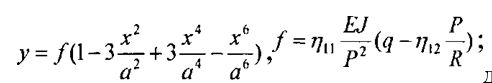
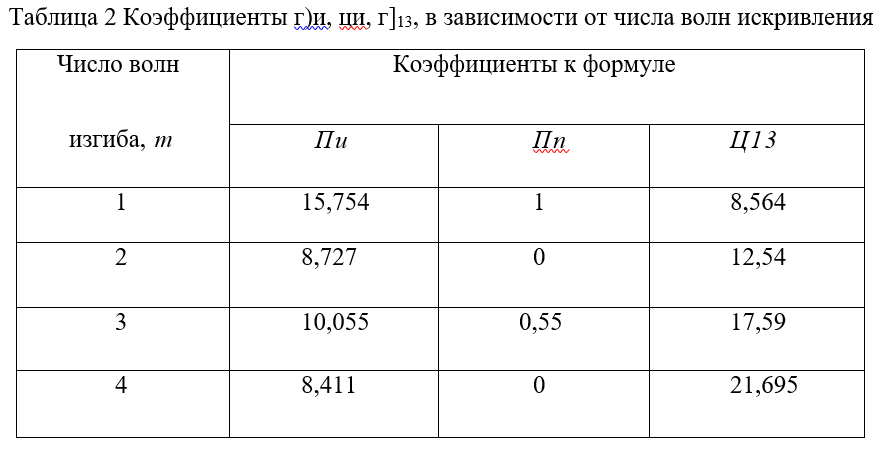
где а = И2, которое удовлетворяет следующим условиям: при х = О, у = /, у’ = 0; при х = ±а, у = у’ = у» = 0. Таким образом кривые, принятые Э. Немешди отвечают реальным условиям изгиба и не имеют скачков кривизны или угла наклона касательной, как кривые решения Г. Мейера и др. Из условий равновесия Э. Немешди нашел расчетную формулу (22)
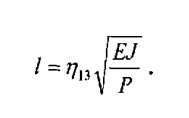
Значения коэффициентов приведены в табл. 2.
В своей работе [16] С. П. Першин сделал расчеты критических сил по всем вышеперечисленным методам с применением различных кривых, описывающих искривленное состояние пути. По результатам расчетов, критические силы Р, полученные при вычислениях с одинаковыми исходными данными, различались на величину АР = ± 5%, что не превышает точность расчетов подобного рода.
Однако у всех описанных выше решений есть ряд существенных недостатков, которые значительно отдаляют результаты расчетов от экспериментально полученных значений критической силы. Самый главный из них — это предпосылка о наличии постороннего силового фактора, выводящего колею из первоначального состояния устойчивого равновесия, который необходим потому, что колея до деформации считается геометрически правильного очертания (идеальная прямая или кривая), следовательно, во всех решениях отсутствует учет начальных неровностей пути, всегда присутствующих на реально существующем пути. Кроме того, в этих решениях не учитывается реальный характер изменения противодействующих искривлению сил — сопротивление сдвигу решетки в балласте и сопротивление повороту шпалы в узлах промежуточных скреплений.
На основе анализа выявленных недостатков С. П. Першин разработал способ решения задачи устойчивости бесстыкового пути темпера- турно-напряженного типа, в котором он, на основе энергетических зависимостей, вывел уравнения, более точно учитывающие реальный характер сил сопротивления изгибу рельсошпальной решетки, а так же ввел в расчет величины начальных неровностей.
Расчет выполняется при следующих начальных предпосылках:
- рельсовая колея имеет отступления от своего геометрически идеального очертания (имеются начальные неровности в плане), которые могут быть выражены математической формулой;
- уравнение изогнутой оси рельса удовлетворяет условиям плавности изгиба колеи. Изгибающий момент и угол поворота изменяется монотонно, без скачков, следовательно, выполняется условие у’= 0, / = 0;
- сопротивление сдвигу шпалы 8 в поперечном оси пути направлении изменяется по линейной зависимости — £ = + К-у, где
(¿о — начальное сопротивление сдвигу, К — коэффициент пропорциональности, у — величина поперечной сдвижки шпалы;
- момент сопротивления повороту рельса в узле скрепления М0 принимается пропорциональным углу поворота сечения в месте закрепления шпалы и определяется зависимостью М0=т0-р, где гп0 — коэффициент пропорциональности, (3 — угол поворота сечения в узле прикрепления рельса.
В основе предлагаемого С. П. Першиным метода расчета лежит принцип возможных перемещений, с помощью которого находится положение равновесия сжатой рельсовой колеи (24)

где с!Ак — элементарная работа сжимающих сил на концах искривления;
с1Аи — элементарная работа деформации изгиба рельсов; с1Аб- элементарная работа по преодолению сил сопротивления балласта при сдвиге;
¿Ас — элементарная работа сил сопротивления, возникающих при повороте шпал в горизонтальной плоскости.
Элементарные работы определяются по следующим формулам
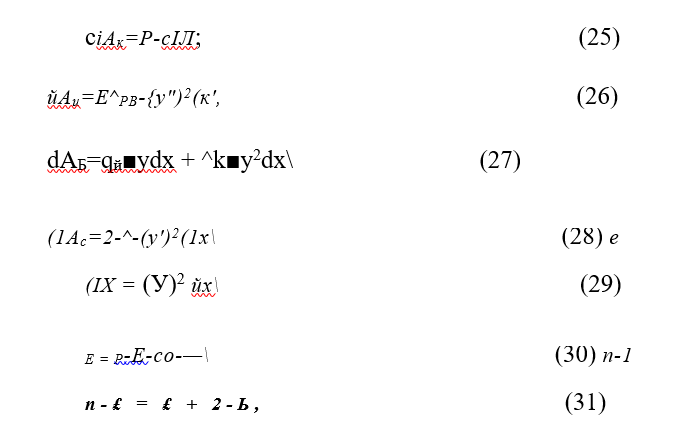
где Р — продольная температурная сила в плети; — продольная сила в плети на концах искривления (с учетом разрядки напряжений за счет удлинения при изгибе);
со — площадь поперечного сечения рельсов;
Лд- момент инерции 2-х рельсов относительно вертикальной оси;
I — длина хорды изогнутой части плети; — длина изогнутой части плети;
Л = (£,-£) — удлинение стержня при деформации;
Ь — длина деформируемых прямолинейных участков стержня;
п — безразмерный коэффициент, выражающий отношение полной длины, на которой происходит деформация, к длине искривленной части стержня;
<7о = (Vе — начальное погонное сопротивление сдвигу шпалы в балласте;
е — междушпальное расстояние (по осям шпал);
к = К/е — погонный коэффициент пропорциональности;
/- стрела изгиба кривой;
г — погонное сопротивление сдвигу рельсов;
У =ЯХ) ~ уравнение функции изогнутой оси рельса;
Полные работы находятся интегрированием элементарных работ с подстановкой различных форм изгиба у =/(х), которые С. П. Першин определял двукратным интегрированием уравнения второй производной с учетом граничных условий: х = ±£/2, у = 0, у’ = 0, у» = 0; при х = 0,у = /,у’ = 0.
В результате интегрирования в зависимости от формы искривления были принятые следующие уравнения изогнутой оси рельса:

На основании вычисленных кривых изгиба и интегрирования формул элементарных работ С. П. Першин получил выражения полных работ (см. таб. 3), в зависимости от формы искривления пути.
| Полные работы | Формы искривления | ||
| Односторонний изгиб на прямой | Двухсторонний изгиб на прямой | Односторонний изгиб на круговой кривой,радиуса Я | |
| Работа сжимающих сил на концах искривления, Ак | 2,757.Р/2+2/о/ / | 12.1613Р/2+2/о/ / | Д2.757/2 +2/о/ + / + 0.4287-) К |
| Работа деформации изгиба рельсов, Аи | 133.567—— /3 | 1 \5ЪА51ЫС | 133.567 £/{2 /3 |
| Работа по преодолению сил сопротивления балласта, Аб | 0.4287</0/7 + + 0.1564к/21 | 0.5135</0/7 + + 0.1997к/21 | 0.4287</0/7 + + 0.1564к/21 |
| Работа по преодолению сил сопротивления скреплений, Ас | 2-2.757 е1 | 2 • 12.1618 е! | 2-2.757т°/2 е! |
Дифференцируя элементарные работы по перемещению: = = можно прийти к выводу, что равенство элементарных работ
В таблице 4, представлены формулы, для вычисления обобщенных сил, в зависимости от различного вида кривой изгиба.
| Обобщенные силы | Формы искривления | ||
| Односторонний изгиб на прямой | Двухсторонний изгиб на прямой | Односторонний изгиб на круговой кривой,радиуса Я | |
| Ок | 2-2.757Р п 1 | /Ч 2/1 2-12.1613Р ■/0 / | 2-Р(2.15Т) ■/0 + / + 0.4287-) 2к |
| О, | 2-133.567 13 | 2-1153.457^ /3 | 2-133.567 ^ |
| <3б | 2 -0.4287^/ + + 2-0.1564кА | 2 -0.5135^/ + + 2-0.1997^/7 | 2-0.4287^/ + + 2-0.1564А/7 |
| <3с | 4-2.757Шо/ е1 | 4-12.16187«о/ е1 | 4-2.757то/ е1 |
Пользуясь данными таблицы 4 можно составлять уравнения равновесия обобщенных сил, которые разрешаются относительно продольной силы. С. П. Першин показал, что сходимость результатов расчета по его методике и результаты моделирования расходятся на 5-8 %, в то же время расчеты, сделанные по методикам, рассмотренным ранее, дают разницу с экспериментальными данными до 100 % и более.
Энергетический метод достаточно точно описывает критическое (конечное) состояние равновесия бесстыкового пути и может быть использован для определения коэффициента устойчивости бесстыкового пути, а так же определения минимально необходимых параметров сопротивления
деформациям решетки из условия обеспечения устойчивости пути от выброса.
К плюсам энергетического метода следует отнести простоту решения и возможность графического анализа состояния бесстыкового пути. Однако существенный недостаток энергетических методов — это полная зависимость точности решения от соответствия принятых уравнений форм изгиба реальному очертанию возможного искривления пути при деформации.
Метод дифференциальных уравнений равновесия
Данный класс методов более точен, т.к. уравнением упругой линии уже не задаются, а оно выводится в ходе решения и полностью соответствует схеме нагружения, что было выполнено в работах Когана А.Я. [7], [20], [21], [22].
Основное дифференциальное уравнение изгиба имеет вид:

Зная выражение для изгибающего момента Мх в любом сечении деформированного пути, получают дифференциальное уравнение в развернутом виде. При этом по концам стержня приходится вводить опорные реакции и опорные моменты.
Методом дифференциальных уравнений пользовались многие ученые, как в России, так и за рубежом, начиная с начала 20 столетия.
Р. Леви составил систему уравнений (37), симметричной половины волны, предполагая, что при волнообразном искривлении реакция балласта в двух крайних четвертях волны уравновешиваются реакциями двух средних четвертей.
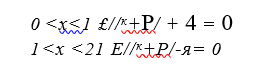
С.И. Морозов предложил расчет устойчивости бесстыкового пути, использующий дифференциальное уравнение изгиба балки:

где ц(у), ш(у’) — реактивная сила и момент; у, уо — суммарные ординаты прогиба и начальных неровностей оси рельсошпалыюй решетки.
В. И. Новакович предложил использовать элементы теории ползучести при расчетах бесстыкового пути методом дифференциальных уравнений [24]. Д. Игнятич в дифференциальных уравнениях устойчивости пути учел неравномерность нагрева плетей [25, 26].
Наиболее полное решение по определению устойчивости бесстыкового пути методом дифференциальных уравнений дано в работах А.Я. Когана [21,22,27].
В основу положена расчетная схема, изображенная на рис. 3.
Поставленная задача была решена при следующих допущениях:
1) продольные силы в обеих нитях одинаковы и постоянны N = const, величина продольной силы при этом равна полусумме факти¬чески действующих в обеих рельсовых нитях сил;
2) радиус кривизны обеих нитей один и тот же р(х), при этом кри¬визна 1/р равна полусумме кривизны наружной и внутренней нитей;
3) при деформации пути шпалы перемещаются параллельно сами
себе.
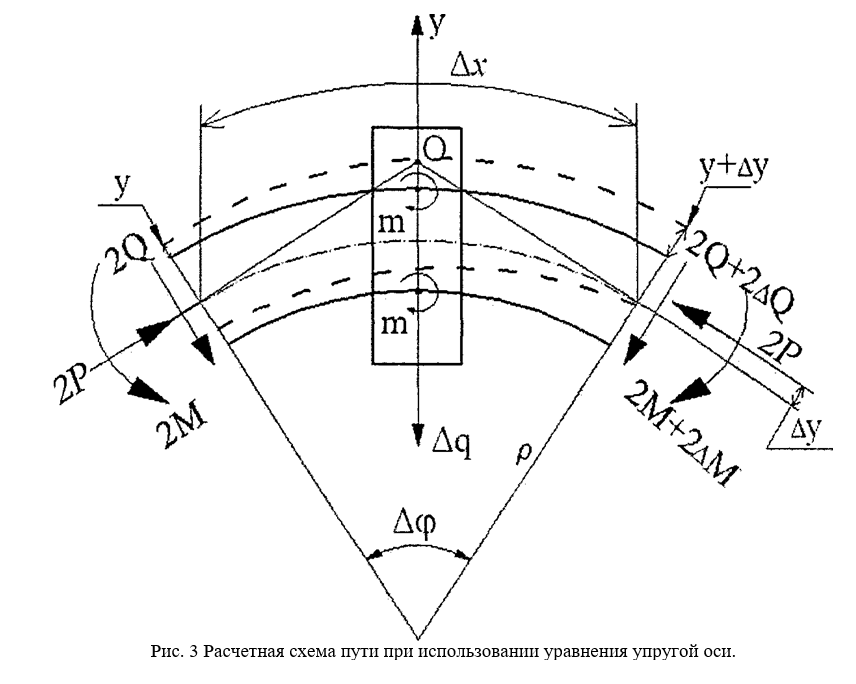
Как следует из второго предположения, изгибающий момент и поперечная сила в обеих рельсовых нитях одинакова.
Вырежем элемент пути Ах, размером, равным расстоянию между соседними шпалами и рассмотрим его равновесие.
Составляя сумму моментов относительно точки О, получим:
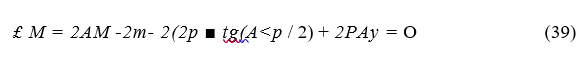
где АМ — приращение изгибающего момента в рельсе на длине Ах; т — момент, прикладываемый к рельсу со стороны скрепления; Дф — угол, стягивающий дугу Ах; Ау — приращение поперечного перемещения рельса на дуге Ах.
Деля равенство (39) на величину 2Ах и учитывая соотношение

Теперь, заменяя отношение приращений отношением дифференциалов и вводя функцию:

где J°z — момент инерции рельса относительно главной вертикальной оси;
X — продольное перемещение сечения рельса.
Вторым членом в соотношении (50) можно пренебречь в связи с его малостью [12]. С учетом всего вышесказанного получим следующее выражение:
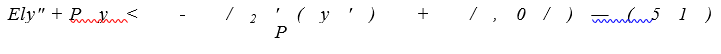
После подстановки: f2(y’)-ry’ и /¡(у) = B-arctg(y/b) в выражение (51) получим основное уравнение устойчивости бесстыкового пути:
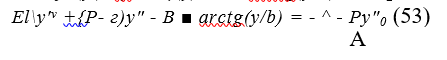
где R — радиус кривой; г, В, Ь — эмпирические коэффициенты к функциям сопротивлений. Решение уравнения (53) без учета начальных неровностей, с помощью системы трансцендентных нелинейных уравнений, было получено проф. А. Я. Коганом в 1963 г.:
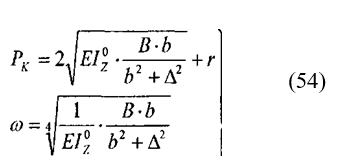
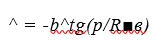
где Рк — продольная критическая сила; со — частота неровности пути; д — неровность пути. В последующих работах уравнение (53) решается с учетом влияния неровностей пути методами определения нелинейной устойчивости. Так, в работе [14] приведено решение с использованием уравнения Матье-Хилла.
Метод имитационного моделирования
Профессором М. Ф. Вериго разработана модель устойчивости бесстыкового пути на основе дифференциального уравнения упругой оси балки, в реализацию и расчетную схему которого были внесены существенные и очень важные изменения.
Он впервые в теории расчетов устойчивости бесстыкового пути разработал математическую модель для получения динамики развития деформаций при потере устойчивости бесстыкового пути. В данной теории можно задать экспериментально полученные, нелинейные по отношению к перемещениям, значения реактивных силовых факторов, промоделировать любую ситуацию, с последующей оценкой ее вероятности и определить необходимые и достаточные условия обеспечения заданного уровня устойчивости бесстыкового пути. Основное отличие этой модели исследования потери устойчивости бесстыкового пути то, что в ней рассматривается динамика процесса деформирования и выброса рельсошпальной решетки.
В качестве основного используется дифференциальное уравнение динамического равновесия (56) элемента бесстыкового пути длиной (см. рис.4), при действии на него продольной температурной силы.
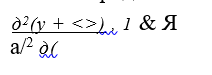
где £ — абсцисса точки на оси пути; ґ- время; у = у(з, ї) — горизонтальное поперечное перемещение оси пути в точке £ в момент времени Ґ.
На основании уравнения (56) было получено решение по методу конечных разностей. Алгоритм этого решения был реализован при создании имитационных моделей работы бесстыкового пути — ИМ1 и ИМ2. Данные модели позволяют проследить цикл работы бесстыкового пути при нагру- жении его продольными и вертикальными силами. В моделях учтена возможность расчета с различными неровностями в плане, а так же неравномерность затяжки гаек клеммных болтов по длине пути.
Результаты расчета выдаются в графическом виде (график распределения перемещений по длине участка моделирования в определенный момент времени, см. рис. 5) и текстовом (таблица результатов расчета).
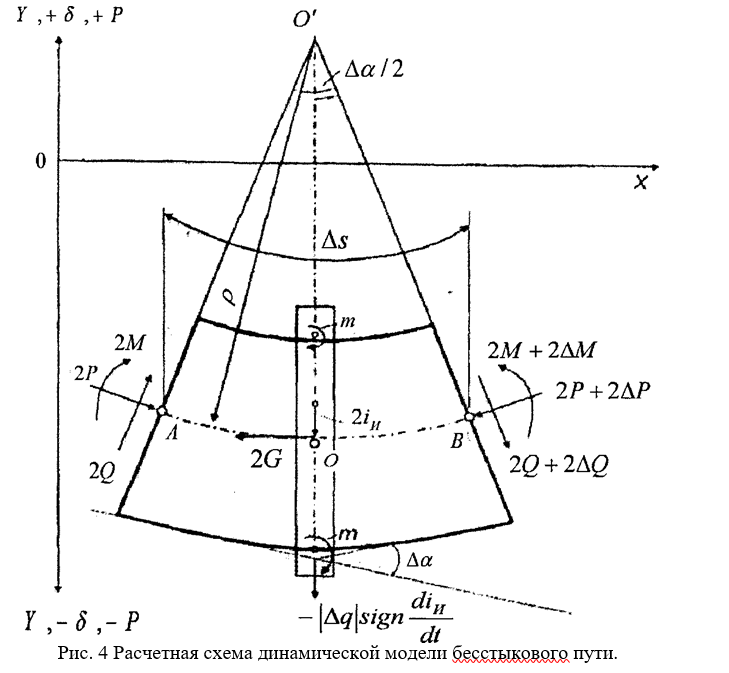

Данная модель работы бесстыкового пути на устойчивость свободна от недостатков энергетических методов, т.к. уравнением изгиба задаваться не приходится, и в отличие от существовавших до этого, решений, основанных на дифференциальных уравнениях, позволяет оценить весь процесс, а не только его конечные состояния.
Метод конечных элементов
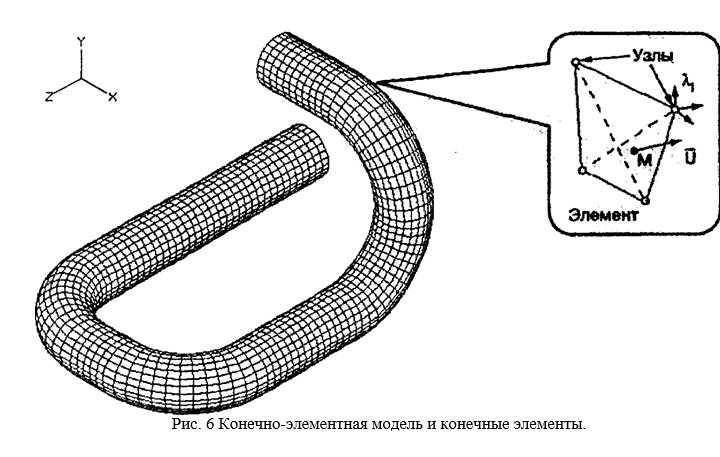
Метод конечных элементов является одной из разновидностей численных методов расчета в механике сплошных сред [35], [36], [37], [38]. Термин «метод конечных элементов» далее МКЭ сейчас применяется для описания очень большой совокупности методов расчета задач, описываемых различными типами уравнений и комбинаций, связанных с рассмотрением в конечном числе точек величин характеризующих состояние системы. При этом обычно, чем больше точек рассматривается, тем точнее получается описание. Во многих задачах, где увеличение числа рассматриваемых точек (далее будет использоваться общепринятый в методе конечных элементов термин «узлы») не ведет к сходимости, могут быть использованы специальные типы конечных элементов, отражающие свойства особенностей, приводящих к сходимости расчетов с использованием стандартных типов элементов.
Метод конечных элементов получил очень широкое распространение и стал одним из основных методов расчета конструкций [39], [40], [41]. Это обусловлено универсальностью подхода, лежащего в основе МКЭ, заключающегося в представлении геометрии любого деформируемого тела в виде совокупности элементов простейшей формы: треугольной, четырехугольной и др. (рис. 6).
Элементы бывают одномерными, плоскими и пространственными, с прямолинейными или криволинейными сторонами. Вдоль каждой из них может быть два или более узлов.
Методом конечных элементов давно и успешно решаются разнообразные задачи расчета, как отдельных элементов конструкции пути, так и рельсошпальной решетки в целом, в частности, задача определения устойчивости бесстыкового пути.
Корейские исследователи К. X. Чу и П. X. Ли [42], предложили конечно-элементную модель бесстыкового пути, которая состоит из 3-х участков: среднего нагруженного, и двух ненагруженных. Каждый участок включает в себя конечные элементы, опирающиеся на упругие пружины, с нелинейными характеристиками, различными для нагруженного и нена- груженного участков.
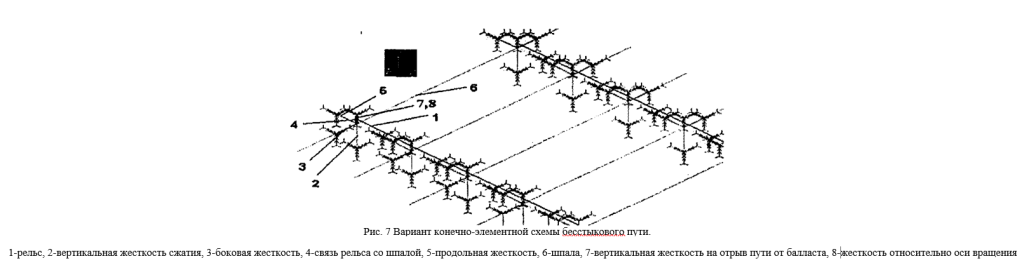
В России известна конечно-элементная модель устойчивости бесстыкового пути, разработанная М. В. Безруковым, в среде конечно- элементного моделирования Cosmos/M, под руководством Э. П. Исаенко [5].
В модели учитывается вертикальная, поперечная и продольная упругость пути и возможность поворота рельса в узле скрепления без отрыва от подкладки. Эта модель для прямых и кривых может учитывать прижатие рельса клеммой скрепления, отступления от норм содержания пути (просадки пути и углы в плане), ослабления пути при производстве работ (количество освобожденных от балласта торцов шпал), многие другие факторы и заметно реагирует на изменение исходных данных в соответствующих областях значений, (см. рис.7).
Вертикальная жесткость пути (при малых вертикальных перемещениях) принята пропорциональной весу шпалы и сопротивлению увлекаемого ею балласта. В зависимости от типа шпалы она изменяется от 50тс/м для железобетонных шпал до 20тс/м для деревянных шпал.
Продольная жесткость пути в модели может быть принята в диапазоне от 50 до 200тс/м.
В результате расчетов были получены формы изгиба при нагревании рельсошпальной решетки в зависимости от плана линии, условий закрепления и расчетных параметров жесткостей. Однако в модели принимаются линейные зависимости сил сопротивления изгибу, что несколько отдаляет полученные расчетом, данные от реальных значений для действующего пути. Принятый метод расчета — Buckling — устойчивость, так же не позволяет проследить весь процесс деформирования бесстыкового пути под действием продольных температурных сил.
Выводы
В данной работе были проанализированы ранее разработанные методы определения усилий, при которых возможна потеря устойчивости бесстыкового пути. Ставится задача выявления дальнейших уточнений решений по определению практических сил, при которых происходит выброс бесстыкового пути, и, что представляется важным для более полного определения роли промежуточных рельсовых скреплений по отношению к этому сложному явлению.
Были рассмотрены основные методы расчета устойчивости бесстыкового пути: энергетический, метод дифференциальных уравнений, метод имитационного моделирования, метод конечных элементов, приведены их теоретические основы. После их рассмотрения и анализа можно сказать, что на современном этапе развития методов расчета бесстыкового пути на поперечную устойчивость каждый из рассмотренных методов обладает как преимуществами, так и недостатками по отношению друг к другу.
— Энергетический метод:
Основное преимущество данного метода — это предельная простота алгебраических решений и возможность быстрого получения критических параметров для бесстыкового пути, а основной недостаток — полная зависимость точности решения от принятых форм изгиба пути. В работах С.П. Першина показано, что разность расчетных параметров с результатами экспериментальных данных, полученных при применении в качестве кривой изгиба одноволновой смещенной синусоиды и при постоянных значениях сил сопротивления перемещениям рельсошпальной решетки, может составлять почти сто процентов. В то же время, применяя созданную им методику вычисления уравнения «составной кривой формы изгиба», он получил разницу с экспериментальными данными в 5-8 %. Данный метод позволяет вычислять предельные значения силовых (критическая продольная сила), и геометрических (длина волны и стрела изгиба), параметров искривлений, без возможности получения промежуточных данных процесса деформирования.
— Метод дифференциальных уравнений:
Основное преимущество данного метода, по сравнению с энергетическим — это независимость точности решения от формы принятого искривления, т.к. форма искривления пути получается в результате расчета, а не задается в начальных условиях. Более точный метод учета разрядки продольных сил в рельсах. Точность решения данного метода определяется точностью решения системы уравнений и точностью исходных данных.
В зависимости от применяемой расчетной схемы можно получить различные расчетные параметры.
Метод имитационного моделирования:
Основное преимущество — переход от уравнений статики к уравнениям динамики, и как следствие, возможность вычисления промежуточных значений параметров деформации пути.
К недостаткам метода можно отнести необходимость применения индивидуальной программы (ИМ-1, ИМ-2) для производства расчетов. К преимуществам — высокое приближение расчетной схемы к реально происходящим процессам и как следствие, высокая точность расчета, а так же возможность прослеживания всего процесса деформирования пути, а не только его конечных или критических параметров.
— Метод конечных элементов:
Основное преимущество — широкий круг решаемых задач, большая наглядность модели и результатов моделирования (возможность просмотра процесса в режиме реального времени), большое количество существующих пакетов для конечно — элементного моделирования (ANSYS, Cosmos, Nastran и др.), общепризнанное лидерство в мире в качестве стандартного метода расчета конструкций и их элементов. К недостаткам данного метода относятся большое количество исходных данных.
В ходе анализа основных методов определения устойчивости бесстыкового пути для выявления дальнейших уточнений решений по определению практических сил, при которых происходит выброс пути, выбран метод дифференциальных уравнений равновесия. Используя предложенный метод можно более подробно определить роль промежуточных рельсовых скреплений в процессе потери устойчивости бесстыкового пути.
Список литературы
- Карейша С. Д. Исторический очерк постепенного развития и улучшения верхнего путевого строения // Тр. НТК НКПС. Вып. 20: Столетие железных дорог. М.: Транспечать НКПС, 1925. С. 175 — 192.
- Чернявский А. Непрерывный железнодорожный путь // Железнодорожное дело. 1903. №4.
- Вериго М. Ф. Новые методы в установлении норм устройства и содержания бесстыкового пути / ВНИИЖТ.- М.: Интекст, 2000. 184 с.
- Першин С. П. Развитие строительно-путейского дела на отечественных железных дорогах. М.: Транспорт, 1978. 296 с.
- Мищенко К. Н. Бесстыковой рельсовый путь. М.: Трансжелдориз- дат, 1950. 62 с.
- Першин С. П. Метод расчета устойчивости бесстыкового пути // Тр. МИИТ. Вып. 147: Путь и путевое хозяйство. М., 1962. С. 28 — 97.
- Коган А. Я. Продольные силы в железнодорожном пути //Тр. ВНИИЖТ. Вып. 332. М.: Транспорт, 1967. 166с.
- Морозов С. И. Устойчивость температурно-напряженного железнодорожного пути: Автореферат докторской диссертации. М.: ВНИИЖТ, 1982. 35 с.
- Нгуен Ван Туен. Определение допускаемой температурной продольной силы на прямых участках бесстыкового пути (на основе теории случайных функций): Автореферат кандидатской диссертации. М.: МИИТ, 1970. 18с.
- Немчек Э. Расчет горизонтальной устойчивости бесстыкового пу¬ти / Перевод ЦНТБ МПС П-7850. 58 с.
- Майер Г. Упрощенный метод теоретического исследования вы¬броса бесстыкового пути / Перевод ЦНТБ МПС, П-8264. 65 с.
- Энгель Э. Устойчивость бесстыкового пути в условиях изменения температуры / Перевод ЦНТБ МПС П-8314. 41 с.
- Мартине А. Выпучивание бесстыкового пути в балласте и рельсы большой длины // Rev. Jen. de Chemins de Fer. 1936 №4. P. 212-231.
- Сакмауэр Jl. Расчет бесстыкового пути на действие продольных сил // Eisenbahntechnische Rundschau. 1960. Т VIII. № 8. S. 389 — 397.
- Нумато М. Сопротивление сварных длинных рельсов продольному изгибу/ Перевод ЦНТБ МПС П-8465. 29 с.