Цикл статей:
Глава 1 – Совершенствование малообслуживаемых рельсовых скреплений для железобетонных шпал бесстыкового пути Глава 3 – Упругие элементы рельсовых скреплений
Кольцевые волнистые шайбы
Расчет волнистых шайб до начала их посадки на опорную плоскость
В современной технике кольцевые волнистые шайбы (рис. 2.1) получают все большее применение и выпускаются самых различных размеров. Пружинящие шайбы представляют собой полого гофрированные кольца прямоугольного поперечного сечения; штампуются из тонкой холоднокатаной стальной ленты (сталь 60С2А) и после термообработки подвергаются заневоливанию.
Ширина прямоугольного сечения колец Ь ориентировочно равна (5-10)8 при внешнем диаметре £)«=(10-18)6, поэтому они могут рассматриваться как кривые брусья. Высота готовых шайб, имеющих п=3-4 полных синусоидальных волн, составляет #=(2~3)6.
Кольцевые волнистые шайбы, компактные по габаритам и простые в из- готовлении, служат надежным упругим элементом, обеспечивающим нужный натяг в различных узлах конструкций. Представляется, что достаточно достоверной расчетной схемой для кольцевой волнистой пружины является плоское кольцо, нагруженное в местах контакта с опорными плоскостями силами, нормальными плоскости кольца, в предположении заделки опорных сечений АА, ВВ, СС… (рис. 2.2, а), за которыми сохраняется при сжатии шайбы лишь свобода для поступательного движения в радиальном направлении. В связи с этим контактные силы в любом из опорных сечений при их приведении к оси кольца сводятся не только к силе Р/п, где Р — полная нагрузка, воспринимаемая шайбой, но и к дополнительному моменту т, препятствующему повороту сечения в соответствующей радиальной плоскости (рис. 2.2, б).
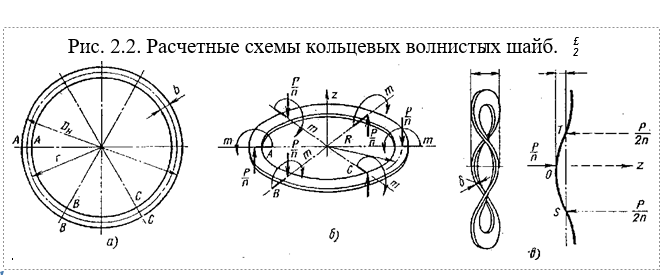
Средний радиус К кольца, представляющего собой развернутую на плоскость волнистую шайбу, несколько больше ее среднего радиуса г (рис. 2.2, а), при расчете этим можно пренебречь.
Расчетная схема, представленная на рис. 2.2, б, является несколько приближенной, но при значительных нагрузках, т. е. в сильно деформированном состоянии, волнистая шайба действительно развертывается почти в плоское кольцо, а расчет конструкций на прочность по размерам в деформированном состоянии, как известно, является более точным, чем расчет по начальным размерам [101].
Некоторые сомнения могут возникнуть при расчете по этой схеме прогиба А, волнистой шайбы, поскольку в рассматриваемом случае имеют место относительно большие перемещения. Однако экспериментально полученные упругие характеристик волнистых шайб до начала посадки гофра на плоскость практически линейны, что позволяет считать перемещения на этом этапе нагружения малыми.
Расчет по принятой схеме показывает, что в сечениях кольца (рис. 2.1, б) возникают изгибающие и крутящие моменты. Их значения определяются после раскрытия статической неопределимости. Крутящие моменты по величине
оказываются меньше изгибающих, но одновременно с последними достигают наибольших значений в опорных сечениях, где поэтому напряжения максимальны [102].
Используя вычисленные значения внутренних силовых факторов и применяя интеграл Мора, можно подсчитать осадку X гофрированной шайбы при ее сжатии. Теоретически построенная упругая характеристика гофрированной шайбы, т. е. зависимость ее осадки от нагрузки, на начальном этапе нагружения (до начала посадки гофра на опорные плоскости) подтверждается экспериментально.
Однако все рабочие формулы, полученные по рассмотренной расчетной схеме, достаточно сложны, и расчет по ним требует довольно много труда и времени. Это заставляет обратиться к более простой, хотя на первый взгляд и более грубой, расчетной схеме. В этом случае полуволна шайбы, ось которой представлена на рис.2.2,в, перекрывающая участок ST и имеющая в развертке длину 1=лг/п, рассматривается как прямая двухопорная балка длиной /, нагруженная в середине пролета силой Р/п [101].
Расчет прост и достаточно точен. Наибольшие напряжения изгиба возникают,
как и у кольца, в сечении, расположенном под точкой приложения силы
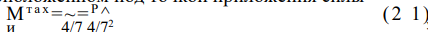
Уменьшение X высоты волнистой шайбы оценивается как двойной прогиб в
середине пролета рассматриваемой балки, т. е.
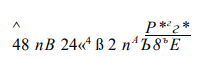
где В — жесткость сечения кольца, при его изгибе из своей плоскости
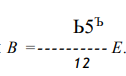
Сопоставляя результаты двух методов расчета, можно отметить, что в первом случае более правильно отражено напряженное состояние волнистой шайбы при ее деформации. В процессе сжатия шайба действительно испытывает одновременно изгиб и кручение, в то время как во втором методе расчета учитывается только один изгиб. Однако можно показать, что последний оказывается несколько завышенным, в связи с чем наибольшие эквивалентные напряжения в опасных точках шайбы в обоих расчетах практически совпадают. Кроме того, расчет на прочность рассматриваемых упругих элементов по номинальным напряжениям является условным, так как волнистые кольцевые пружины подвергаются пластическому обжатию (заневоливанию).
Что касается жесткости шайбы, подсчитываемой по первому и второму методам расчета, то в обоих случаях получается почти один и тот же результат. В связи с этим расчет волнистых шайб целесообразно вести по расчетной схеме (рис. 2.2в). Этот подход достаточно хорошо отражает их поведение при сжатии, и в то же время он более простой. Поэтому его и следует рекомендовать для инженерной практики.
Таким образом, осадку волнистой шайбы X до начала посадки гофра на опорную плоскость можно определить по формуле (2.2), которая достаточно хорошо подтверждается экспериментом. На начальном участке характеристика волнистой пружины действительно практически линейна. Заметное искривление наблюдается лишь с момента начала посадки гофра на опорные плоскости.
Исследование посадки волнистой шайбы на опорную плоскость
Примем приближенно, что волна гофра является дугой окружности, поэтому легко определить ее радиус.
Начало посадки наступает в сечении наибольшего Ми при силе Ршъ которая определяется из условия
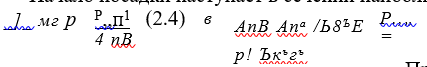
При нагрузке Р>Рип когда гофр на участках длиной 5 с каждой стороны от вершины волны О (рис. 2.2,в) уже сел на опорную плоскость, сближение опорных плоскостей по принятой упрощенной схеме будет
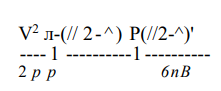
где сила Р связана с длиной ^ зависимостью
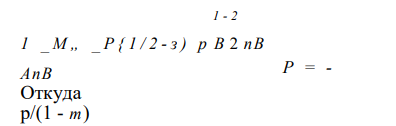
где т = 2^/7 — коэффициент посадки гофра на плоскость; 2з — участок дуги, пришедшей в соприкосновение с опорной плоскостью на длине полуволны I (см. рис. 2.2, в).
Первое слагаемое формулы (2.6) выражает свободное поступательное движение сечений гофра до их прихода в соприкосновение с опорной плоскостью на участке 5. Второе слагаемое определяет сближение опорных плоскостей, вызванное поворотом сечений в месте посадки сечений гофра из наклонного до перпендикулярного положения к опорной плоскости. Третье слагаемое — это перемещение в связи с изгибом еще не осевшей части гофра (балки).
После преобразования формулы (2.6) получим
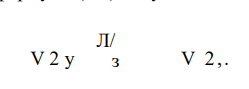
В начале посадки, когда т = О, Я = Ли п = — / (см. выше). В конце посадки т = 1, Я = Я = /, а Рд = да
Исключая из формул (2.8) и (2.9) коэффициент посадки т, получаем уравнение характеристики волнистой шайбы, связывающей нагрузку и перемещение на последнем участке деформирования шайбы от начала ее посадки, когда Р = Рп.н., ДО ПОЛНОГО сплющивания при Р = Рпред,
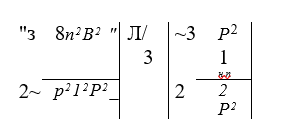
Теоретическая характеристика хорошо согласуется с экспериментальной.
Однако рассчитывать на идеальное совпадение теории с практикой в условиях посадки вряд ли возможно. Ничтожно малые зазоры, теоретически еще сохраняющиеся между опорными плоскостями и гранями сложным образом деформированной шайбы при нагрузках, близких к предельным, частично перекрываются. Это связано с наличием допусков на все размеры шайбы и недостаточно качественным ее изготовлением. Этим же объясняется также, некоторый разброс точек в криволинейной части характеристики при повторных на- гружениях, что связано и с нестабильностью сил трения, возникающих на поверхности соприкосновения шайбы с опорными плоскостями при ее сплющивании. Силами трения объясняется небольшая петля гистерезиса, наблюдаемая в процессе нагружения и разгрузки шайбы (рис. 2.3) [101].
Расчет волнистых шайб в связи с их пластическим обжатием
Переходя к расчету волнистых шайб на прочность, заметим, что коэффициент запаса прочности г] у заневоленных шайб следует определять не по напряжениям, а путем сравнивания предельной относительной линейной деформации термообработанной пружинной ленты 8пРеД «2,5-3,0% с максимальной деформацией Бтах > £т, возникающей при первой развертке волнистой шайбы-заготовки на плоскость етах ~8/2р0 в связи с ее заневоливанием (1 /р0 наибольшая кривизна гофра шайбы-заготовки).
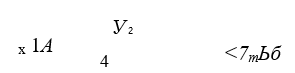
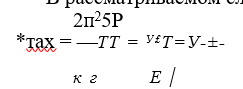
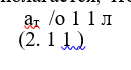
В рассматриваемом случае предполагается, что кривизна гофра у шайбы- заготовки постоянна. Используя формулу (2.3), имеем (У— предельно возможный прогиб шайбы-заготовки при заневоливании путем полного ее обжатия). Тогда

где Д — пластическая осадка шайбы-заготовки при заневоливании; V > 1 — коэффициент степени заневоливания (у = ^- = — «2.0-2.5, где ? — высота упругого слоя в прямоугольном сечении шайбы толщиной 8).
Таким образом, высота шайбы-заготовки Н = Б+8, а радиус ее гофра
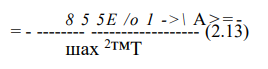
Из работы [102] по диаграмме пластически деформируемого материала без упрочнения с пределом текучести ат в изогнутом за предел упругости брусе прямоугольного поперечного сечения шириной Ъ и толщиной 8 изгибающий момент
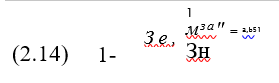
При разгрузке и выходе шайбы из плоскости кривизна образующегося гофра готовой шайбы

Откуда по формулам (2.14) и (2.15)

Максимально возможная осадка готовой волнистой шайбы

высота готовой волнистой шайбы с учетом зависимостей (2.3) и (2.16)
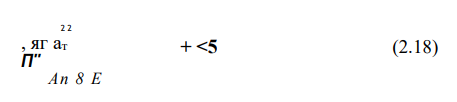
Пластическая осадка шайбы при заневоливании по формулам (2.12) и (2.17)
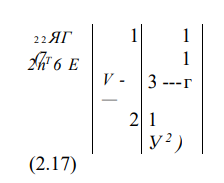
Результаты расчета гофрированных шайб
Произведем расчет двух гофрированных шайб диаметром Вн = 70 мм, толщиной 8— 5 мм для стыковых болтов и второй шайбы наружным диаметром Д, = 50 мм, толщиной 8= 3 мм для клеммных и закладных болтов. Численные значения параметров этих шайб согласно рис 2.2 приведены в табл. 2.1.
Уменьшение высоты волнистых шайб Я до начала их посадки на опорную плоскость определяем по формуле 2.2. При этом значение модуля упругости стали Е = 2 • 105 Мпа. Расчетная нагрузка для шайб под гайки стыковых болтов Р ~ 80 кН, а для клеммных и закладных болтов Р = 20 кН. Упругая осадка шайб под гайки стыковых болтов Я = 1,7 мм, а для клеммных и закладных болтов Я = 0,3 мм.
Нагрузку, при которой начинаются посадки волнистых шайб на опорную плоскость, определяем по формуле (2.5). Для стыковых болтов Рнп = 168 кН; для клеммных и закладных Рнп = 22 кН.
| Назначение шайб. | Численные значения параметров, мм. | ||||||
| Бн | Бв | 5 | в | г | f | п | |
| Для стыковых | |||||||
| болтов. | 70 | 28 | 5 | 21 | 38,5 | 1 | 3 |
| Для клеммных и | |||||||
| закладных болтов. | 50 | 23 | 3 | 13,5 | 18,2 | 1 | 3 |
Наибольшую пластическую осадку, которую могут выдержать шайбы без разрушения, определим по формуле (2.19). Для шайб под гайки стыковых болтов Д = 1,5 мм, а шайб под гайки клеммных и закладных болтов А = 0,6 мм.
Высоту волнистых шайб определяем по формуле (2.18). Для стыковых болтов Ь = 7 мм. Для клеммных и закладных болтов Ь = 3.7 мм.
Полную высоту шайб с учетом их возможных пластических деформаций определяем по формуле (2.19). Для стыковых болтов Н = 7 + 1,5 = 8,5 мм. Для клеммных и закладных болтов Н = 3.7 + 0,6 = 4,3 мм.
Тарельчатые пружины
Конструкция, изготовление и назначение тарельчатых пружин
Тарельчатые пружины (рис. 2.3) штампуются из листовой стали в форме оболочки, имеющей вид усеченного конуса (угол подъема 0=2-6°; ^ « 2.0-3.0).
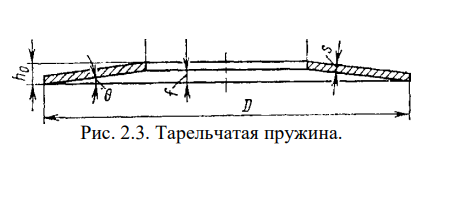
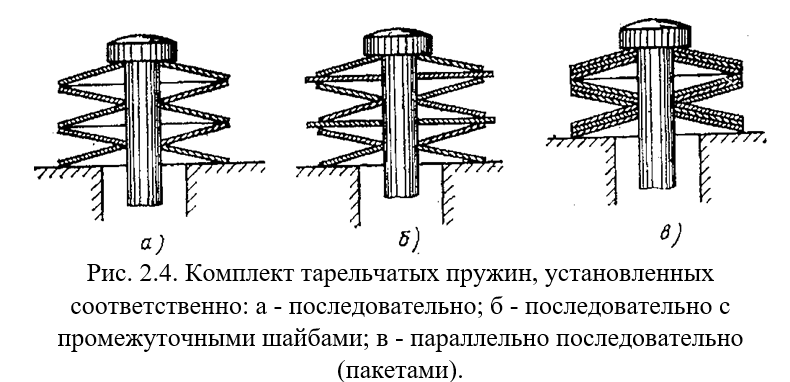
В ГОСТ 3057-79 включены тарельчатые пружины диаметром 0=28-300 мм из листовой стали толщиной 1-20 мм, с габаритной высотой конуса \ =0.6-9.0 мм. Наибольшая сжимающая рабочая нагрузка, воспринимаемая этими пружинами, достигает 52*104Я. Сжимающие усилия Р, распределенные равномерно по периметру кромок (наружной и внутренней), изгибают стенки оболочки и уменьшают угол подъема 0. Осадка одной тарелки при этом не должна превышать 0,8/ где/- высота внутреннего конуса (см. рис. 2,3), так как при большей осадке жесткость тарелки резко возрастает в связи с отгибом ее внутренней кромки внутрь и переносом в связи с этим сжимающего усилия Р на больший диаметр [103]. Для получения нужного осевого перемещения упругий элемент составляется из ряда секций, каждая из которых образуется двумя тарелками, соприкасающихся наружными кромками. Секции монтируются в гильзе или на общей центрирующей оправке (рис. 2.4,а).
Отдельные секции взаимодействуют. Соприкасаясь внутренними кромками. Образуемые таким образом весьма жесткие конструкции предназначаются для восприятия больших усилий и используются, главным образом, как мощные буферные пружины во всякого рода амортизаторах.
Для большего гашения энергии ударов, воспринимаемых пружинами, между тарелками можно устанавливать шайбы диаметром > О (рис. 2.4,6). В этом случае жесткость конструкции еще несколько возрастает за счет сил трения, развивающихся на внешних кромках тарелок при их скольжении по шайбам. При наличии особо больших нагрузок пружины можно устанавливать пакетами, вкладывая конус в конус так, чтобы верхняя тарелка своей внутренней поверхностью ложилась на наружную поверхность нижней тарелки (рис. 2.4,в) при этом рабочая нагрузка может быть увеличена примерно пропорционально числу пружин в пакете.
Тарельчатые пружины изготавливают из листовой стали марки 60С2А по ГОСТ 14959-79 или других равноценных по механическим свойствам марок. Листы стали должны иметь чистую поверхность. Пружины из листов толщиной до 6 мм штампуются в холодном состоянии.
Предварительно из листов вырезаются полосы-заготовки, из которых вырубаются шайбы; последние выгибают на специальных штампах.
Пружины, подвергнутые термообработке, должны иметь мелкозернистую структуру и твердость НЯС = 44-50. Поверхность пружины очищают от окалины и заусенцев травлением, пескоструйным аппаратом и обработкой на наждачных кругах. Острые углы кромок закругляются с радиусом 0,1 б.
Периметры опорных кромок пружин повышенной прочности шлифуются наждачными кругами. Ширина опорных плоскостей пружин в зависимости от наружного диаметра приведена в ГОСТ 3057-79.
Заключительной технологической операцией изготовления жестких тарельчатых пружин является их нагружение до полного сплющивания, при котором они получают, как правило, некоторую пластическую осадку; в этом состоянии их выдерживают определенное время. Эта операция называется заневоливанием, которое повышает несущую способность тарельчатых пружин в пределах упругости, если при эксплуатации сохраняется нормальная температура. Никакая термообработка после пластического обжатия не допускается. Если при обжатии возникают пластические деформации, то высота пружины-заготовки должна быть несколько больше высоты пружины по чертежу.
При приемке пружины подвергают внешнему осмотру и проверяют по размерам. Допуски и размеры тарельчатых пружин приведены в ГОСТ 3057-54. Там же указаны технические условия приемки и испытаний тарельчатых пружин.
Расчет тарельчатых пружин
Тарельчатая пружина представляет собой малоподъемную коническую оболочку, которая при деформации получает большие перемещения.
Расчет тарельчатых пружин в такой строгой постановке -задачи был разработан В.И. Феодосьевым [104]. Однако для конструкции пружин, встречающихся
в практике, с отношением диаметров
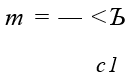
можно довольствоваться более простым приближенным методом расчета, опирающимся на предположение о недеформируемости меридионального сечения диска. Ниже излагается именно этот приближенный метод.
Рассмотрим тарельчатую пружину (рис. 2.5,а), нагруженную силой Р (силу Р будем считать положительной в том случае, когда она стремится уменьшить угол 9).
Примем, что меридиональное сечение пружины в процессе деформации не искривляется, а лишь поворачивается как жесткое целое около неподвижной точки О. Это предположение оправдывается тем лучше, чем меньше отношение т=Б/с1 и больше толщина диска б.
Допустим, что под нагрузкой Р меридиональное сечение пружины, не изменяя в соответствии с принятой гипотезой своей формы, повернулась на угол а около некоторой точки О, находящейся на расстоянии с от оси пружины (рис. 2.5,а).
Выберем вспомогательную систему координат ху с началом в координат в точке О (ось х направим параллельно образующей конических поверхностей тарелки). При повороте сечения на угол а (рис. 2.5,а) некоторая точка А с координатами х, у, которой остаются неизменными, приблизиться к оси пружины на величину 5 (рис. 2.6,а):
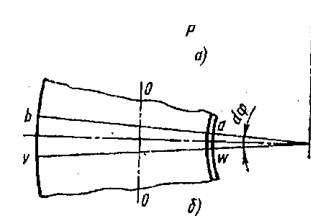
Рис. 2.5. Схема поворота

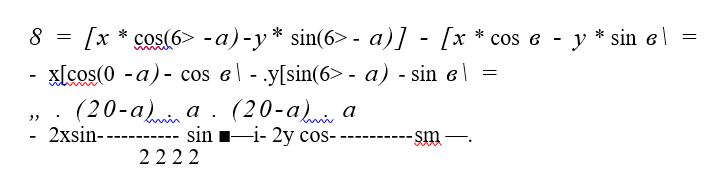
Из-за малости углов в и а можно принять, что
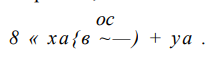
Относительная линейная деформация в окружном направлении в точке А на расстоянии р от оси диска (рис. 2.6,6)
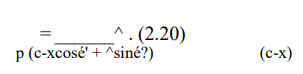
Относительная линейная деформация в направлении осей л: и у в соответствии с принятой гипотезой о неизменности меридионального сечения во внимание не принимается. Рассматривается тело пружины как кольцевой брус, нормальные напряжения в меридиональном сечении в соответствии с законом Гука
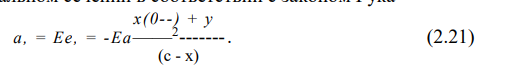
Из условия равновесия полутарелки, нагруженной вертикальными силами, видно, что равнодействующая всех внутренних сил в меридиональном сечении равна нулю, т.е.

Это условие позволяет определить величину с.
Действительно, подставим в зависимость (2.22) выражение для напряжения (2.21) и выполним интегрирование.
Полагая по-прежнему приближенно, что Бтв~вп соубМ, имеем
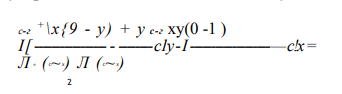
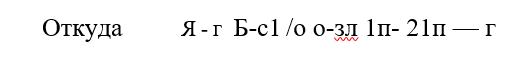
где В-2Я и ¿-2г — наружный и внутренний диаметр пружины.
Разлагая 1пОМ при И/с1> 1 в ряд, можно показать, что точка поворота О лежит несколько ближе к оси пружины, чем центр тяжести Н меридионального сечения тарелки (рис. 2.5,а). Двумя меридиональными (по условию симметрии — главными) сечениями, образующими угол ¿(р, выражен элемент тарелки аЪуу? (рис. 2.5,6). Сумма моментов всех сил, действующих на выделенный элемент аЪ\ж относительно оси 00 (рис. 2.5,6), дает (рис. 2.6,6)
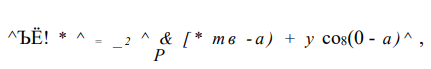
или, учитывая малость углов 9 и а, имеем 4яг ^
Подставляя в последнюю зависимость выражение (2.21) для напряжения <тп получаем
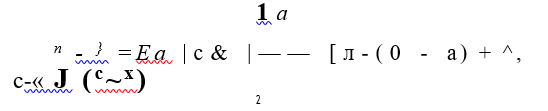
откуда, выполняя интегрирование, имеем
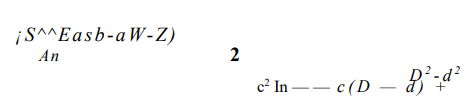
После подстановки в последнее выражение с по формуле (2.4) получим
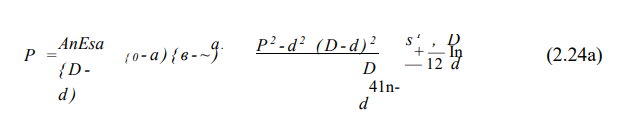
Заменяя 0 и а выражениями 2f/(D-d) и 2Я, /(D — ¿7) соответственно, где f — начальная высота внутреннего конуса, а Я/ — осадка одной тарелки, имеем
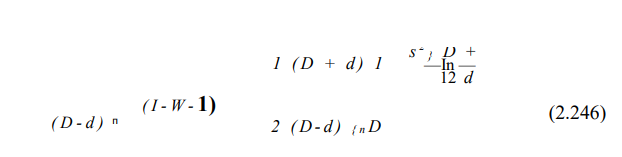
Решение обратной задачи, т.е. определение величины осадки пружины по заданной нагрузке, приводят к значительно большим вычислительным трудностям, так как требует решения кубического уравнения. В этом случае удобно предварительно построить характеристику пружины, т.е. начертить в координатах (Я/, Р) график, представляющий связь осадки Я1 и усилия Р по формуле (2.25); необходимые величины определяют по этому графику.
Характеристики, построенные по уравнению (2.25), представлены на рис. 2.5. Их вид в сильной степени зависит от толщины тарелки
Проследим изменение осадки Я/ по виду характеристики пружины.
Вид характеристики тарельчатой пружины, т.е. ее жесткость, в сильной степени зависят от отношения 2=/%, где/- полная высота внутреннего конуса.
При 2 < 42 осадка жесткой тарельчатой пружины с увеличением нагрузки Р монотонно возрастает. В этом случае характеристика представлена на рис. 2.7 кривой ОИ.
При 2 >42 осадка с увеличением нагрузки монотонно растет только до известной ее величины Ра (рис. 2.7). при этой нагрузке тарелка уже заметно теряет свою конусность.
Как следует из рис. 2.7, в рассматриваемом случае перемещения, превышающие Ла, соответствуют нагрузкам меньшим, чем Ра.
При Я>Ла на характеристике пружины проявляется участок с отрицательной производной, который можно назвать участком отрицательной жесткости. В этом случае характеристика тарельчатой пружины представлена на рис. 2.7 точками О, а, с, е, / От точки а к точке е происходит внезапное увеличение перемещения X. Имеет место скачок на величину ае, после чего с увеличением нагрузки прогибы продолжают монотонно расти. Характеристика пружины при нагрузке представлена на рис. 2.7 точками £ е, с, а, к, О, при этом на участке ск опять имеется скачок в уменьшении перемещений.
У гибких тарельчатых пружин при условии, что г > 242, характеристика, построенная по формуле (2.25), имеет вид, представленный на рис. 2.7 линией ОАВСЭЕР, причем деформированное состояние пружины на участке характеристики ABC является неустойчивым. Это проявляется во внезапном скачкообразном росте осадки при возрастании нагрузки больше Ра.
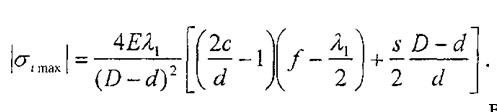
Осадка стремительно возрастает на значительную величину, изображенную в масштабе на рис. 2.7 отрезком АЕ. Происходит выщелкивание. Пружина получает обратную конусность и вновь способна нести нагрузку. При дальнейшем увеличении нагрузки прогиб пружины будет опять возрастать монотонно, чему соответствует ветвь характеристики EF.
При разгрузке и уменьшении силы Р до нуля осадка убывает лишь до величины OD, и разгруженная пружина остается в выщелкнутом положении. Чтобы вернуть ее в исходное состояние, направление нагрузки Р следует изменить на обратное, что на графике (рис. 2.7) отразится переходом FD в область отрицательных ординат (кривая DC).
Когда эта новая «отрицательная» нагрузка достигнет некоторой величины Рс, деформированное состояние тарельчатой пружины станет вновь неустойчивым и опять произойдет скачок, при котором перемещение внезапно уменьшится на величину СК. После этого скачка в перемещении пружина принимает вид первоначального усеченного конуса. Однако, находясь под нагрузкой «отрицательного направления», высота конуса будет несколько больше, чем заданная. При уменьшении нагрузки Р до нуля тарелка вернется к своим исходным размерам (участок характеристики КО).
Гибкие тарельчатые пружины находят применение в автоматических устройствах, связанных с внезапным включением и выключением системы.
В общем машиностроении обычно используют тарельчатые пружины, у которых Z « л/2.
Для жестких тарелок первым слагаемым в квадратных скобках формулы (2.25) можно пренебречь.
Напряжение а, в меридиональном сечении диска пружины определяется по
формуле (2.21). Выражая в ней углы айв, учитывая их малость, через осадку тарелки Я/ и начальную высоту внутреннего конуса f соответственно, как это делалось выше, имеем
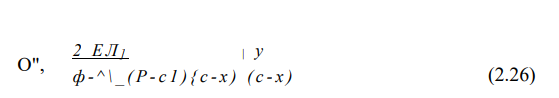
На рис. 2.8 представлены эпюры изменения напряжений по контуру меридионального сечения диска (Л]</). Наибольшее по абсолютной величине напряжение (напряжение сжатия) возникает в верхней точке 1 внутренней кромки (при х = с-с1 /2, у = 5/2).
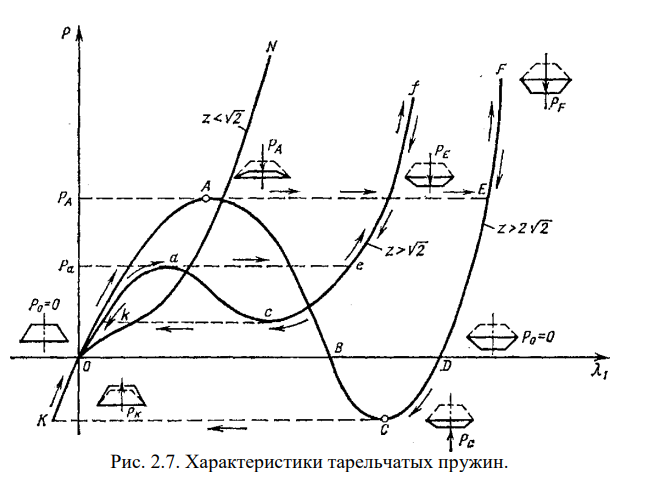
По толщине внутренней кромки тарельчатой пружины напряжения изменяются по линейному закону. Наибольшие напряжения возникают в нижней точке 2 внутренней кромки (при х=с-ё/2, у=-з/2).
Из сказанного следует, что предусмотренное ГОСТ 3057-79 скругление острых углов у кромок диска является весьма рациональным, так как этим устра
няются зоны, в которых возникают пики напряжений. Для тарельчатых пружин значения напряжений, получаемые по формуле (2.26), практически условны.
Это объясняется тем, что, как уже указывалось, все тарельчатые пружины, как правило, подвергаются пластическому обжатию.
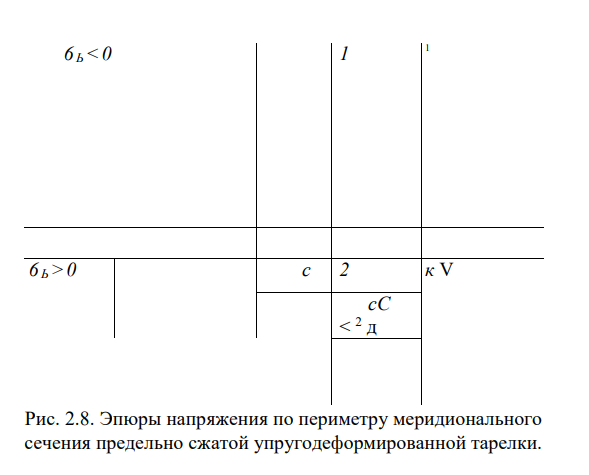
В связи с этим создается поле остаточных напряжений, имеющих в опасных точках А и В направление, противоположное направлению напряжений, возникающих при рабочей нагрузке. Таким образом, благодаря обжатию истинные напряжения заметно меньше напряжений, получаемых по формуле (2.26). При ее применении в расчетах приходится брать условные допускаемые напряжения, значительно превышающие предел текучести, а иногда предел прочности используемой стали. Однако такого рода расчет по условным напряжениям вряд ли может быть рекомендован.
Для установления величины истинных напряжений необходимо изучить остаточные напряжения, возникающие в связи с пластическим обжатием пружины. Теоретическое исследование этого вопроса впервые проведено В.И. Фео- досьевым [104]. Однако расчет пластического обжатия тарельчатых пружин представляет собой достаточно сложную задачу, поэтому в инженерной прак
тике обычно ограничиваются подбором тарельчатых пружин непосредственно по рабочей нагрузке Р, руководствуясь при этом заранее разработанными и экспериментально апробированными таблицами, одна из которых имеется в ГОСТ 3057-54. В упомянутых материалах указана также и упругая осадка (например, Л]=0,8/), которую способна дать одна тарельчатая пружина при рабочей нагрузке.
Руководствуясь заданной величиной требуемой полной осадки, можно установить, число тарельчатых пружин, обеспечивающих совместно необходимую жесткость упругого элемента в целом.
Результаты расчета тарельчатых шайб
Проведем расчет двух тарельчатых шайб диаметром Он = 70 мм, толщиной 8 = 5 мм для стыковых болтов и второй шайбы наружным диаметром Д, = 50 мм, толщиной 8-3 мм для клеммных и закладных болтов. Расчетные параметры этих шайб согласно рис 2.3 приведены в табл. 2.2.
Величину нагрузки, необходимой для получения заданной величины осадки шайбы АЛ, определим по формуле (2,25).
При этом значение модуля упругости стали Е = 2 • 105 МПа.
| Назначение | Численные значения | параметров, мм. | ||||||
| шайб. | Вп | Бв | 5 | £ | 11 | 1ю | п | |
| Для стыковых болтов. | 70 | 28 | 5 | 3,0 | 2,0 | 8,0 | 3 | |
| Для клеммных и закладных болтов. | 50 | 23 | 3 | 2,0 | 1,5 | 5,0 | 3 | |
В результате расчета нагрузка, необходимая для получения упругой осадки шайбы, для клеммных и закладных болтов величиной 1,5 мм составляет Р = 20,3 кН.
Расчетная нагрузка для получения упругой осадки шайбы под гайку стыкового болта величиной 2,0 мм получилась Р = 61,6 кН.
Напряжение растяжения в верхней точке внутренней кромки шайбы определяем по формуле (3,7а).
Для стыковых болтов сг, = 4782 МПа. Для клеммных и закладных болтов
^ ‘пш
а, -4150 МПа.
Напряжения получились больше, но это свидетельствует лишь о том, что шайбы под расчетной нагрузкой будут иметь остаточные деформации.
Расчеты упругих шайб для клеммных, стыковых и закладных болтов показали, что в основу их конструкции должны быть положены тарельчатые пружины с размерами для стыковых болтов: наружный диаметр Б = 70 мм, внутренний диаметр ё = 28 мм, толщиной 5 = 5 мм, стрела подъема £ = 3 мм. Для клеммных и закладных болтов: наружный диаметр Б = 50 мм, внутренний диаметр с1 = 23 мм, толщиной 8 = 3 мм, стрела подъема f = 2 мм.
Для повышения упругости и виброустойчивости тарельчатые шайбы должны быть волнистыми (гофрированными) с высотой волны в обоих случаях 2мм.
В этом случае общая высота шайбы для стыковых болтов составит Ь = 10 мм, а для клеммных и закладных болтов Ь = 7 мм.
Лабораторные испытания тарельчатых гофрированных пружин
Методика испытаний
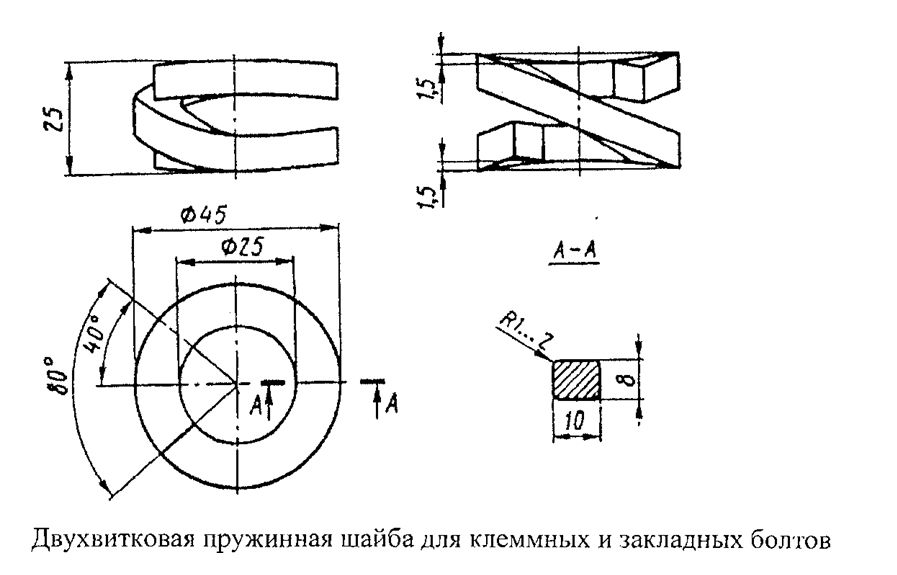
Объектом испытаний явились: типовые пружинные двухвитковые шайбы для клеммных и закладных болтов рис 2.9, типовые тарельчатые пружины для стыковых болтов, выполненные согласно ТУ 32 ЦП-749-86; опытные гофрированные тарельчатые пружины для стыковых болтов внешним диаметром 70 мм, внутренним — 28 мм, толщиной — 5 мм со стрелой подъема 3 мм и высотой волны — 2 мм; опытные гофрированные тарельчатые пружины для клеммных и закладных болтов внешним диаметром 50 мм, внутренним диаметром — 23 мм, толщиной 3 мм со стрелой подъема 2 мм и высотой волны — 2 мм.
В соответствии со стандартом СТ ССФЖТ ТМ 04.04.-97 величина жесткости определялась в рабочем диапазоне нагрузок для пружин под стыковые болты от 20 до 50 кН и для пружин под гайки клеммных и закладных болтов от 10 до 25 кН.
На испытательной машине ПСУ-50, аттестованной согласно ГОСТ 24.55581 заводской номер 2374, год выпуска 1959, снималась диаграмма нагрузка- деформация. Скорость перемещения нагружающего устройства — 5 мм/сек с одновременной регистрацией величины сжатия пружин индикатором часового типа с ценой деления 0.01 мм согласно ГОСТ 3057-79.
По результатам испытаний составлялись протоколы испытаний и строились графики зависимости величины сжатия от прилагаемой нагрузки.
Результаты испытаний
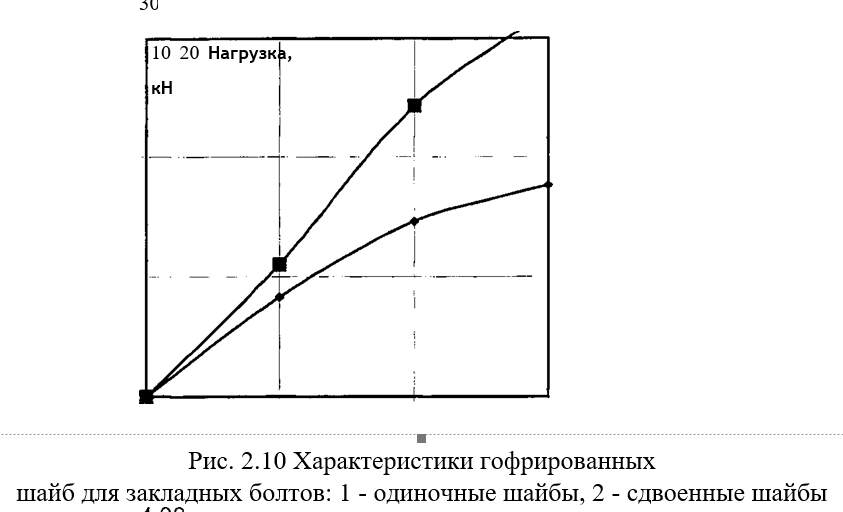
Результаты испытаний двухвитковых пружинных шайб приведены в табл. 2.3, а данные для тарельчатых и тарельчатых гофрированных пружин приведены в табл. 2.4 и 2.5. При этом в табл. 2.4 приведены результаты испытаний шайб толщиной 2 мм. Гладкие тарельчатые пружины оказались недостаточно упругими, а гофрированные тарельчатые пружины толщиной 2 мм в рабочем диапазоне нагрузок «потекли» — получили большие остаточные деформации. В дальнейшем шайбы изготавливали из листовой стали 60С2А толщиной 3 мм. Результаты испытаний этих шайб, приведены в табл. 2.5 и на рис. 2.10, показали, что жесткость одиночных пружин составила 12 кН/мм (12 т/см), а сдвоенные гофрированные шайбы имеют жесткость 8 кН/мм (8 т/см).
Эта жесткость удовлетворяет техническим требованиям на упругие тарельчатые шайбы, утвержденные С.А. Рабчуком 15.12.1998г.
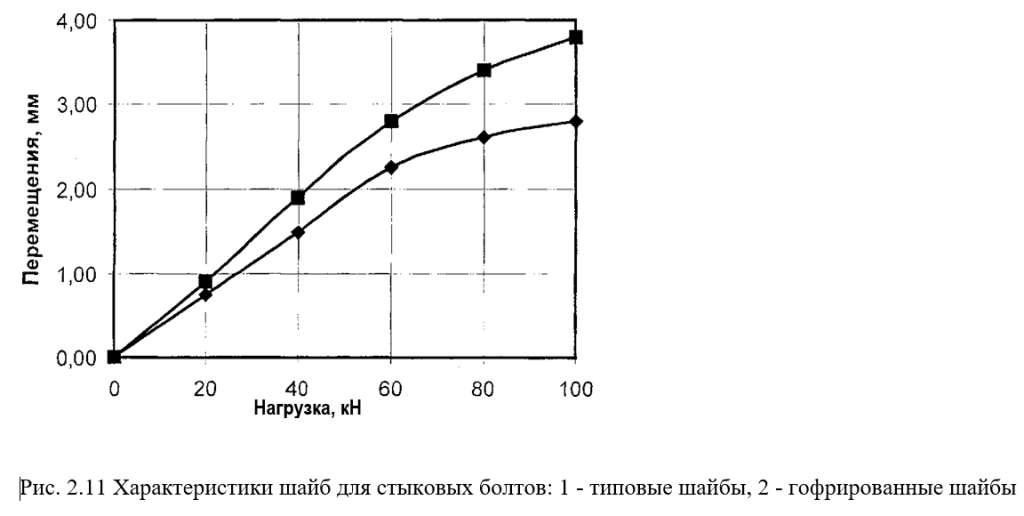
Результаты испытаний тарельчатых типовых и гофрированных шайб для стыковых болтов приведены в табл. 2.6 и 2.7 и на рис 2.11.
Эти результаты свидетельствуют о том, что жесткости типовых пружин равна 24 кН/мм, и опытных гофрированных — 19 кН/мм (19 т/см), что соответствует техническим требованиям.
Таким образом, для обеспечения упругости клеммы и закладных соединений в скреплениях КБ следует применять упругие гофрированные шайбы толщиной 3 мм, внешним диаметром 50 мм и внутренним диаметром 23 мм, а под гайки стыковых болтов наряду с типовыми тарельчатыми пружинами можно применять гофрированные тарельчатые шайбы толщиной 5 мм, внешним диаметром 70 мм и внутренним диаметром 28 мм.
| Нагрузка кН | Номера шайб | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Среднее | |
| Перемещение точек приложения силы, мм (ветвь нагрузки) | |||||||||||
| 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 1.85 | 2.00 | 1.68 | 1.61 | 2.25 | 2.27 | 2.80 | 2.23 | 1.58 | 1.52 | 1.98 |
| 10 | 3.31 | 4.20 | 3.55 | 3.32 | 4.31 | 4.02 | 3.92 | 4.32 | 3.81 | 3.54 | 3.83 |
| 15 | 3.71 | 4.55 | 4.81 | 3.87 | 4.68 | 4.35 | 4.71 | 4.64 | 4.04 | 4.62 | 4.40 |
| 20 | 3.94 | 4.82 | 4.46 | 4.06 | 4.92 | 4.54 | 4.98 | 4.85 | 4.26 | 5.09 | 4.59 |
| 25 | 4.18 | 5.06 | 4.65 | 4.22 | 5.07 | 4.72 | 5.15 | 5.08 | 4.50 | 5.31 | 4.79 |
| 30 | 4.42 | 5.27 | 4.85 | 4.42 | 5.22 | 4.85 | 5.37 | 5.24 | 4.68 | 5.52 | 4.98 |
| Перемещение точек приложения силы, мм (ветвь разгрузки) | |||||||||||
| 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 2.51 | 2.48 | 2.21 | 1.76 | 2.87 | 2.30 | 2.68 | 2.08 | 1.98 | 2.26 | 2.31 |
| 10 | 3.65 | 4.55 | 3.99 | 3.68 | 4.51 | 4.12 | 4.62 | 4.38 | 3.98 | 4.29 | 4.18 |
| 15 | 4.04 | 4.81 | 4.45 | 4.08 | 4.78 | 4.48 | 4.92 | 4.79 | 4.23 | 4.96 | 4.55 |
| 20 | 4.18 | 4.98 | 4.60 | 4.22 | 4.94 | 4.64 | 5.08 | 4.96 | 4.44 | 5.32 | 4.74 |
| 25 | 4.31 | 5.11 | 4.70 | 4.33 | 5.11 | 4.74 | 5.24 | 5.10 | 4.52 | 5.46 | 4.86 |
| 30 | 4.42 | 5.27 | 4.85 | 4.42 | 5.22 | 4.85 | 5.37 | 5.24 | 4.68 | 5.52 | 4.98 |
| № пп | Бн мм | ёвн мм | Толщина мм | Высота, мм | Нагрузка, кН. Деформация, мм | Примечание | ||||||
| До испытаний | После испытаний | 5 | 10 | 15 | 20 | 25 | 30 | |||||
| (шайбы гладкие тарельчатые) | ||||||||||||
| 1 | 50 | 23 | 2,0 | 7,5 | 7,1 | 0,08 | 0,42 | 0,72 | 1,10 | 1,40 | 1,82 | |
| 2 | 50 | 23 | 2,0 | 7,5 | 7,0 | 0,04 | 0,55 | 0,80 | 1,22 | 1,52 | 1,91 | |
| 3 | 50 | 23 | 2,0 | 7,5 | 7,1 | 0,08 | 0,51 | 0,81 | 1,18 | 1,48 | 1,88 | |
| 4 | 50 | 23 | 2,0 | 7,5 | 7,1 | 0,10 | 0,42 | 0,72 | 1,02 | 1,42 | 1,80 | |
| 5 | 50 | 23 | 2,0 | 7,5 | 6,9 | 0,10 | 0,52 | 0,82 | 1,15 | 1,45 | 1,88 | |
| 6 | 50 | 23 | 2,0 | 7,5 | 7,0 | 0,04 | 0,48 | 0,79 | 1,17 | 1,47 | 1,87 | |
| 7 | 50 | 23 | 2,0 | 7,5 | 7,0 | 0,08 | 0,43 | 0,75 | 1,15 | 1,45 | 1,87 | |
| 8 | 50 | 23 | 2,0 | 7,5 | 7,1 | 0,08 | 0,56 | 0,82 | 1,43 | 1,47 | 1,92 | |
| 9 | 50 | 23 | 2,0 | 7,5 | 6,9 | 0,10 | 0,46 | 0,81 | 1,18 | 1,46 | 1,87 | |
| 10 | 50 | 23 | 2,0 | 7,5 | 7,0 | 0,08 | 0,53 | 0,84 | 1,21 | 1,50 | 1,90 | |
| (шайбы гофрированные) | ||||||||||||
| 1 | 50 | 23,1 | 2,0 | 8,6 | 7,4 | 0,10 | 0,96 | 1,75 | 2,26 | Потекла при 2,2 т | ||
| 2 | 50 | 23,1 | 2,0 | 9,0 | 7,5 | 0,12 | 0,98 | 1,68 | 2,18 | При 2,4 | ||
| -> л | 50 | 23,2 | 2,0 | 9,0 | 7,6 | 0,08 | 1,00 | 1,81 | 2,31 | При 2,2 | ||
| 4 | 50 | 23,2 | 2,0 | 9,0 | 7,4 | 0,12 | 1,12 | 1,91 | 2,42 | При 2,1 | ||
| 5 | 50 | 23,2 | 2,0 | 9,0 | 7,7 | 0,08 | 0,96 | 1,78 | 2,28 | При 2,4 | ||
| 6 | 50 | 23,2 | 2,0 | 9,2 | 7,7 | 0,12 | 0,97 | 1,77 | 2,45 | При 2,2 | ||
| 7 | 50 | 23,2 | 2,0 | 8,7 | 7,5 | 0,10 | 0,95 | 1,75 | 2,48 | При 2,2 | ||
| 8 | 50 | 23,1 | 2,0 | 9,1 | 7,6 | 0,10 | 1,08 | 1,85 | 2,42 | При 2,2 | ||
| 9 | 50 | 23,2 | 2,0 | 9,1 | 7,7 | 0,08 | 1,12 | 1,91 | 2,40 | При 2,2 | ||
| 10 | 50 | 23,1 | 2,0 | 9,0 | 7,6 | 0,12 | 1,10 | 1,88 | 2,35 | При 2,3 | ||
| № пп | Бн мм | ёвн мм | Толщина мм | Высота, мм | Нагрузка, кН. Деформация, мм | Высота после испытаний | ||||||
| До испытаний | После испытаний | 5 | 10 | 15 | 20 | 25 | ||||||
| (одинарные шайбы) | ||||||||||||
| 1 | 50.5 | 22,9 | 3,2 | 8,8 | 8,5 | 0,10 | 0,75 | 1,10 | 1,58 | 1,78 | 8,1 | |
| 2 | 50,6 | 22,9 | 3,2 | 8,8 | 8,0 | 0,08 | 0,70 | 1,20 | 1,70 | 1,90 | 7,9 | |
| 50,4 | 22,9 | 3,2 | 8,8 | 7,9 | 0,08 | 0,50 | 0,98 | 1,60 | 1,80 | 7,7 | ||
| 4 | 50,6 | 22,9 | 3,2 | 8,8 | 8,5 | 0,10 | 0,58 | 1,05 | 1,60 | 1,80 | 8,2 | |
| 5 | 50,3 | 22,9 | 3,2 | 8,8 | 8,3 | 0,05 | 0,35 | 0,78 | 1,30 | 1,50 | 8,3 | |
| 6 | 50,2 | 22,9 | 3,2 | 8,8 | 7,5 | 0,04 | 0,50 | 0,98 | 1,60 | 1,80 | 7,5 | |
| 7 | 50,3 | 22,9 | 3,2 | 8,8 | 7,6 | 0,46 | 0,90 | 1,50 | 2,20 | 2,40 | 7,5 | |
| 8 | 50,2 | 22,9 | 3,2 | 8,8 | 8,3 | 0,48 | 1,00 | 1,48 | 2,00 | 2,20 | 8,0 | |
| 9 | 50,4 | 22,9 | 3,2 | 8,8 | 8,2 | 0,18 | 0,68 | 1Д4 | 1,60 | 1,80 | 7,9 | |
| 10 | 50,3 | 22,9 | 3,2 | 8,8 | 8,4 | 0,16 | 0,64 | 1,12 | 1,80 | 2,00 | 8,2 | |
| ср | 50,4 | 22,9 | 3,2 | 8,8 | 8,1 | 0,17 | 0,66 | 1,13 | 1,70 | 1,90 | 7,9 | |
| (сдвоенные шайбы) | ||||||||||||
| 1-2 | 50,5 | 22,9 | 3,2 | 13,2 | 13,2 | 0,60 | 1,35 | 2,00 | 2,85 | 3,40 | 13,2 | |
| 3-4 | 50,5 | 22,9 | 3,2 | 13,3 | 13,2 | 0,10 | 0,65 | 1,40 | 2,00 | 2,40 | 13,1 | |
| 5-6 | 50,3 | 22,9 | 3,2 | 13,3 | 13,2 | 0,08 | 0,80 | 1,50 | 2,20 | 2,60 | 13,1 | |
| 7-8 | 50,3 | 22,9 | 3,2 | 13,3 | 13,3 | 0,06 | 0,80 | 1,50 | 2,20 | 2,60 | 13,1 | |
| 9-10 | 50,4 | 22,9 | 3,2 | 13,2 | 13,1 | 0,20 | 0,80 | 1,60 | 2,30 | 2,75 | 13,1 | |
| ср | 50,4 | 22,9 | 3,2 | 13,3 | 13,2 | 0,21 | 0,90 | 1,60 | 2,30 | 2,75 | 13,1 | |
Испытания упругих гофрированных шайб на циклическую нагрузку
Испытания проводились на универсальной испытательной машине ГРМ-1 с пульсатором, заводской № 132, год выпуска 1957. Измерения проводились штангенциркулем № Е-50701.
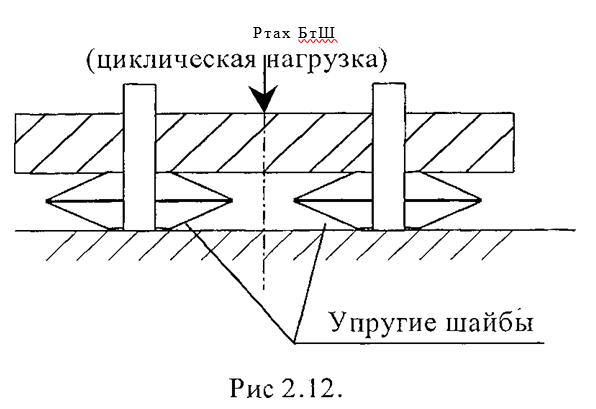
На циклическую нагрузку испытывались 4 сдвоенные упругие гофрированные шайбы. Схема испытаний приведена на рис. 2.12. Параметры цикла нагру- жения Ртах = 4 тс, Рпнп = 2 тс. Циклическая частота нагружения — 600 цикл/мин. База испытаний 10 тыс. циклов. Результаты обмера образцов приведены в табл. 2.8. Таким образом циклические испытания показали, что тарельчатые гофрированные шайбы под гайки стыковых, клеммных и закладных болтов скрепления КБ выдержали циклические испытания без повреждений, при минимальных остаточных деформациях.
| № пп | Бн мм | <1вн мм | Тол щи- на мм | Высота, мм | Нагрузка, кН. Деформация, мм | Высота после испытаний | ||||||||
| До Исп | осле исп. | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |||||
| 1 | 69,5 | 28,3 | 4,98 | 10,0 | 9,1 | 0,87 | 1,22 | 1,70 | 2,12 | 2,60 | 2,88 | 3,10 | 3,25 | 9,0 |
| 2 | 69,5 | 28,2 | 4,98 | 10,0 | 8,8 | 0,54 | 1,00 | 1,40 | 1,68 | 2,30 | 2,54 | 2,62 | 2,73 | 8,5 |
| 3 | 69,5 | 27,9 | 5,00 | 10,5 | 9,0 | 0,00 | 0,54 | 0,88 | 1,38 | 1,76 | 2,12 | 2,38 | 2,50 | 8,8 |
| 4 | 69,5 | 28,0 | 5,00 | 10,2 | 8,0 | 0,08 | 0,50 | 0,88 | 1,35 | 1,52 | 1,68 | 1,78 | 1,86 | 7,5 |
| 5 | 69,5 | 28,0 | 5,00 | 10,2 | 9Д | 0,00 | 0,35 | 0,68 | 1,10 | 1,62 | 2,00 | 2,34 | 2,56 | 9Д |
| ср | 69,5 | 28,1 | 5,00 | 10,2 | 9,0 | 0,28 | 0,72 | 1,11 | 1,56 | 1,96 | 2,24 | 2,44 | 2,58 | 8,6 |
| Таблица 2 Результаты лабораторных испытаний гофрированных шайб для стыковых болтов | ||||||||||||||
| № пп | Эн мм | <1вн мм | Толщина мм | Высота, мм | Нагрузка, кН. Деформация, мм | Высота после испытаний | ||||||||
| До Исп. | осле исп. | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |||||
| 1 | 70,0 | 28,1 | 5,0 | 11,0 | 10,1 | 0,80 | 1,41 | 1,90 | 2,55 | 3,10 | 3,45 | 3,75 | 3,90 | |
| 2 | 70,1 | 28,1 | 5,0 | 11,0 | 9,8 | 0,60 | 1,20 | 1,70 | 2,25 | 2,75 | 3,05 | 3,15 | 3,28 | |
| 3 | 70,1 | 28,0 | 5,0 | 11,5 | 10,0 | 0,10 | 0,72 | 1,10 | 1,68 | 2,15 | 2,55 | 2,85 | 3,40 | |
| 4 | 70,0 | 28,1 | 5,0 | 11,2 | 9,0 | 0,12 | 0,62 | 1,10 | 1,65 | 1,85 | 2,10 | 2,60 | 3,12 | |
| 5 | 69,8 | 27,9 | 5,0 | 11,2 | 10,1 | 0,15 | 0,45 | 0,90 | 1,35 | 2,05 | 2,40 | 2,90 | 3,50 | |
| Ср | 70,0 | 28,1 | 5,0 | 11,2 | 9,8 | 0,35 | 0,88 | 1,35 | 1,90 | 2,40 | 2,80 | 3,05 | 3,45 | |
| Номер образца | Маркировка | Наружный диаметр Бн, мм | Внутренний диаметр ёвн, мм | Толщина ^ мм | Высота сдвоенных шайб, мм | |
| До испытаний | После исп ытаний | |||||
| 1 | 1/2 | 50,5 | 22,9 | 3,2 | 13,2 | 13,1 |
| 2 | 3/4 | 50,4 | 22,9 | 3,2 | 13,1 | 13,1 |
| 3 | 5/6 | 50,2 | 22,9 | 3,2 | 13,1 | 13,0 |
| 4 | 7 /8 | 50,2 | 22,9 | 3,2 | 13,1 | 13,0 |
тых шайб для стыковых болтов
Эксплуатационные испытания гофрированных шайб
Для эксплуатационных испытаний в соответствии с ТУ ЦП 531 «Пружины тарельчатые гофрированные», утвержденные 31.05.1999г заместителем руководителя Департамента пути и сооружений МПС России В. И. Андреенко. Было изготовлено 100 тарельчатых гофрированных шайб диаметром 70 мм под гайки стыковых болтов и 200 штук диаметром 50 мм под гайки клеммных и закладных болтов.
Перед установкой в путь все шайбы были подвергнуты испытаниям на
прочность путем трехкратного обжатия на прессе ПСУ-50 с усилием 80 кН (8 тонн) гофрированных шайб диаметром 70 мм и усилием 25 кН (2,5 тоны) — диаметром 50 мм. Все шайбы испытывались на прочность выдерживанием. Для эксплуатационных испытаний был выбран оптимальный участок с бесстыковым путем, железобетонными шпалами и промежуточным скреплением КБ. Участок располагался на двух уравнительных пролетах на перегоне Инская — Чемская на первом пути с грузонапряженостью 75 млн. тонн брутто.
Установка шайб в путь была осуществлена 20.10 1999 г, о чем имеется соответствующий акт, подписанный начальником дистанции пути А.П. Козловым. При установке гофрированных шайб затяжка стыковых болтов осуществлялась крутящим моментом 600 Нм, закладных 150 Нм.
Во время установки сломалась одна шайба диаметром 70 мм на стыковом болте. Во время опытной эксплуатации изломов шайб не отмечено. Контрольные промеры затяжки стыковых и закладных болтов динамометрическим ключом показали их стабильные натяжения.
Таким образом эксплуатационные испытания упругих гофрированных шайб диаметром 70 мм под гайки стыковых болтов на уравнительных пролетах бесстыкового пути и диаметром 50 мм под гайки закладных болтов течение двух месяцев, когда по опытному участку попущено 6,3 млн. тонн груза, показали их высокую эксплуатационную надежность.
Выводы
В целях снижения затрат на содержание рельсовых скреплений бесстыкового пути поставлена задача перейти на упругие гофрированные тарельчатые шайбы, устанавливаемые под гайки стыковых, клеммных и закладных болтов.
В результате проведения теоретических, лабораторных и натурных исследований были получены следующее результаты:
Теоретические расчеты показали, что в качестве упругих пружин под гайки стыковых болтов могут быть использованы или типовые тарельчатые шайбы или гофрированные шайбы, в основу которых положены типовые.
В качестве упругих пружин под гайки клеммных и закладных болтов приняты тарельчатые гофрированные шайбы из стали 60С2А толщиной 3 мм, внешним диаметром 50 мм и внутренним диаметром 23 мм. Высота волны таких шайб должна быть 2 мм.
Лабораторные испытания шайб внешним диаметром 50 мм, внутренним диаметром 23 мм и толщиной 3 мм показали, что одиночные шайбы обеспечивают жесткость 12 кН/мм, а сдвоенные 8 кН/мм (8 т/см) и удовлетворяют техническим требованиям.
В качестве упругих пружин под гайки стыковых болтов приняты тарельчатые гофрированные шайбы из стали 60С2А толщиной 5 мм, внешним диаметром 70 мм и внутренним диаметром 28 мм. Высота таких шайб 10 мм.
Лабораторные испытания показали, что жесткость гофрированных шайб составляет 19 кН/мм (19 т/см), что соответствует техническим требованиям.
Динамические испытания на пульсаторе тарельчатых гофрированных шайб диаметром 70 мм и толщиной 5 мм, а также сдвоенных гофрированных шайб диаметром 50 мм и толщиной 3 мм показали хорошие результаты.
Эксплуатационные испытания гофрированных шайб диаметром 70 мм под гайки стыковых болтов и диаметром 50 мм под гайки клеммных и закладных болтов скрепления КБ на двух уравнительных пролетах бесстыкового пути после пропуска 6,3 млн. тонн брутто груза показали высокую эксплуатационную надежность и стабильность натяжения ботов.
Таким образом, для обеспечения упругости клеммных и закладных соединений в скреплениях КБ следует применять упругие гофрированные шайбы из стали 60С2А толщиной 3 мм, внешним диаметром 50 мм и внутренним диаметром 23 мм. Под гайки стыковых болтов наряду с типовыми тарельчатыми шайбами можно применять тарельчатые гофрированные шайбы толщиной 5 мм, внешним диаметром 28 мм и полной высотой пружины 10 мм.
Список литературы
- Жилин Г.К. Настечик Н.П. Теоретические исследования работы скреплений под нагрузкой на стрелочном переводе с железобетонными брусьями // Сб. науч. тр. / ДИИТ. — 1975. — Вып. 167/16. — С. 87-97.
- Климов В.М. Настечик Н.П. Исследование работы скрепления типа КБ // Сб. науч. тр. / ДИИТ. — 1976. — Вып. 180/17. — С. 46-57.
- Климов В.М.. Настечик Н.П.. Исследование характеристик жесткости скрбплений для пути с железобетонным подрельсовым основанием // Сб. науч. тр. / ДИИТ. — 1977, — Вып. 188/18. -С. 48-53.
- Гасанов А.И. Хазинский Н.М. Влияние промежуточных рельсовых скреплений на неравноупругость пути с железобетонными шпалами // Сб. науч. тр. / МИИТ. — 1979. — Вып. 607. — С. 55-60.
- Гасанов А.И.. Демидов A.A. К вопросу об оптимизации формы нашпаль- ных прокладок повышенной упругости // Сб. науч. Тр. / МИИТ. — 1979, — Вып. 607. — С. 61-65.
- Лысюк B.C. Методы расчета жесткости пути // Сб. науч. тр. / ВЗИИТ. — 1979.-Вып. 99. — С. 22-36.
- Железобетонные шпалы для рельсового пути / Под ред. проф. А.Ф.Золотарского. — М.: Транспорт. 1980. — 270 с.
- Лысюк B.C. Книга о путейских и инженерных традициях // Путь и путевое хозяйство. — 1979. — № 2. — С. 28-29.
- Радычук В.А. Теоретические исследования оптимального модуля упругости подрельсового основания и узла скрепления в вертикальной плоскости при железобетонных шпалах // Сб. науч. тр. / ДИИТ. — 1974. — Вып. 151. — С. 98-108.
- Демидов A.A. Эффективность работы промежуточных рельсовых скреплений с прокладками повышенной упругости в пути с железобетонными шпалами.: Автореф. дисс. … канд. техн. наук. — М.: 1973. — 24 с.
- Радычук В.А. Исследование основных оптимальных-расчетных параметров промежуточных скреплений для железобетонных шпал.: Автореф. дис. … канд. техн. наук. — Днепропетровск, 1975. — 24 с.
- Васин A.B., Жарпов В.М. Исследование ослабления затяжки гаек на бесстыковом пути со скреплением КБ и ЖБ // Сб. науч. тр. / МИИТ. — 1973. — Вып. 446. — С. 70-78.
- Воробейчик Л.Я., Радычук В.А. Расчет оптимальной жесткости элементов узла скрепления при железобетонных шпалах // Сб. науч. тр. / ДИИТ. — 1975. — Вып. 167/16. — С. 20-24.
- Шульга В.Я., Лаптев В.А. Фактическая эффективность бесстыкового пути с железобетонными шпалами при прокладках повышенной упругости // Сб. науч. тр. / МИИТ. — 1977. — Вып. 556. — С. 38-46.
- Шахунянц Г.М. Кондратьев A.A. Изменение монтажных сил в закладных и клеммных болтах под поездной нагрузкой // Сб. науч. тр. / МИИТ. — 1973. — Вып. 382. — С. 126-136.
- Андреев Г.Е. Совершенствовать конструкцию скреплений // Путь и путевое хозяйство. — 1978. — № 1. — С. 22-24.
- Шахунянц Г.М.. Демидов A.A. Гасанов А.И. Нужны пружинные элементы // Путь и путевое хозяйство. — 1978. — № 3. — С. 35-37.
- Сливец Д.П. Чтобы путь был бархатным // Путь и путевое хозяйство. — 1978.-№8.-С. 20-21.
- Белый В.И., Крутиков A.M., Григорьев О.В. Как улучшить скрепление КБ // Путь и путевое хозяйство. — 1978 — № 9. — С. 36-37.
- Лысюк B.C., Кравченко Н.Д. Основные требования — прочность и надежность // Путь и путевое хозяйство. — 1978. — № 11. — С. 22-23.
- Лападус Т.А. Скрепление для высокоскоростных линий // Путь и путевое хозяйство. — 1978. — № 12. — С. 30-31.
- Иванов А.Г. О влиянии изгиба рельса от боковой силы на угон пути // Сб. науч. тр. / ДИИТ. — 1979. — Вып. 204/21. — С. 98-109.
- Першин С.П. Развитие строительно-путейского дела на отечественных железных дорогах. — М.: Транспорт, 1978. -296 с.
- Крутиков A.M. Нужны резиновые прокладки // Путь и путевое хозяйство. — 1973.-№3,-С. 40.
- Евдокимов Б.А. Эффективное средство улучшения работы скреплений // Путь и путевое хозяйство. — 1972. — № 4. — С. 8-10.
- Шахунянц Г.М., Демидов А. А., Гасанов А.И. К вопросу об эффективности применения нашпальных резиновых прокладок повышенной упругости в скреплении КБ // Сб. науч. тр. / МИИТ. -1979.- Вып. 607. — С. 36-54.
- Петров Н.В. На основе исследований опыта // Путь и путевое хозяйство. — 1979. — № 4. — С. 23.
- Кравченко Н.Д. Роль скрепления в обеспечении стабильности колеи при высокоскоростном движении поездов // Некоторые задачи механики скоростного наземного транспорта. — Киев. Наукова думка. 1974. — С. 96-101.
- Волошко Ю.Д. К вопросу о зависимости затрат труда на текущее содержание пути от скорости движения грузовых поездов // Сб. науч. тр. / МИИТ. — 1979.-Вып. 646.-С. 104-111.
- Петров Н.В., Купцов В.В., Лозовская М.И. Совершенствование существующих и разработка новых конструкций промежуточных рельсовых скреплений для железобетонных шпал. // Совершенствование рельсовых скреплений. М, 1979, С.10-39.
- Афанасьев. В.Ф., Воробейник Л.Я., Гасанов А.И., Демидов А А. К определению некоторых динамических параметров промежуточных скреплений для технических требований на их проектирование // Исследование воздействия на путь современного подвижного состава. Днепропетровск, 1986. С. 100-1 10
- Технические требования к промежуточным рельсовым скреплениям ЦП 1-86. МНС, ВНИИЖТ. М., 1987. 9 с.
- Ханна А.И. Анализ работы скреплений железобетонных шпал // Железные дороги мира. 1983, № 4, с. 44-48.
- Тенденции в выборе рельсовых скреплений // Железные дороги мира. 1995, № 1, с.46-48.
- Шарапов С.П., Афанасьев В.Ф. Разработка и внедрение рельсовых скреплений // Железнодорожный транспорт. 1996, № 7, с. 47-51.