Аналитические решения задач взаимодействия колеса и рельса

Граничные условия для бесконечной балки (для простоты записи иногда индексы опускаем):0(0,8) = ОА^_х 8) – ф(0, 8)) = Р(8) / 2 , ф(0,8)=0, ф(а),8)=0, 1(00,8) = 0.

Изгибающий момент выражается такой зависимостью: М = Е1 аналогичная зависимость и для изображений по Лапласу. Опуская промежуточные выкладки, запишем изображение изгибающего момента и поперечной силы.

Граничные условия для полубесконечной балки с силой Р на конце: Q(0, s) = GAf_xx (|'(0, s) – ф(0, s)) = P(s), M(0,s) = EI_ycp'(0,s) = 0,9(oo,s) = 0,|(oo,s) = 0.

К сожалению, получить соответствующие оригиналы в аналитической форме не удается. Поэтому придется использовать алгоритмы численного обращения преобразования Лапласа.

Модели Рэлея и Эйлера

Все получаемые выражения имеют одинаковую форму записи, однако, корни характеристических уравнений различаются.

Отметим, что с помощью известных формул Эйлера от экспоненциальных функций можно перейти к тригонометрическим. Получаем такие выражения.

Q(z,s) = P(s) -A(z) Модель Эйлера, бесконечная балка.

Нетрудно заметить, что по внешнему виду приведенные выражения в области изображений напоминают соответствующие выражения в задачах статики. В этом имеется вполне здравый смысл. Комплексная величина Б является функцией параметра преобразования Лапласа б. Если положить б=0, то мы автоматически придем к статической задаче.

Задача изгиба с кручением в горизонтальной плоскости

При наличии относа и виляния подвижного состава приходится рассматривать пространственное изгибно-крутильное движение рельса. Уравнения при поиске решений в виде экспонент приводят к такому характеристическому уравнению.

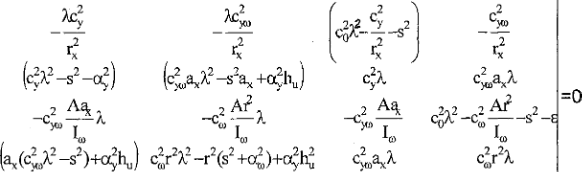
Раскрывая этот определитель, приходим к алгебраическому уравнению восьмой степени относительно параметра X. Ввиду этого при построении расчетного алгоритма необходимо предусмотреть дополнительные процедуры поиска комплексных корней этого характеристического уравнения. Это существенно усложняет расчет, но в принципе эта трудность преодолима. Задача о пространственном движении рельса может быть решена до конца с помощью предлагаемого в данной работе метода.

Аналитические выражения реакции рельса в оригиналах при плоском изгибе

Выражение для оригинала в аналитической форме удается получить только для модели Эйлера в случае ъ = 0. Выражение для поперечной силы в сечении г=0 очевидно:

(Х0,г) = Р(1)/2

Выражения для прогиба, изгибающего момента и поперечной силы получены нами с помощью таблиц [54]. Они приведены также в работе Г.Б. Муравского [87]. Используя эти выражения, можно решать уравнение удара в нелинейной форме методом Эйлера.

Основное напряженно-деформированное состояние идеального рельсового пути при равномерном качении колесной пары

При качении колесной пары по рельсовому пути в рельсах возникает напряженно-деформированное состояние. Его параметры могут быть определены из решения соответствующей динамической задачи. Как показано в работе С.П. Тимошенко [104, 106], при равномерном качении колесной пары без дефектов по идеальному рельсу можно искать напряженно-деформированное состояние, решая статическую задачу. При этом следует иметь в виду, что решение будет записываться в подвижной системе координат, начало которой совпадает с точкой контакта колеса с рельсом. Получив решение статической задачи, в него следует ввести коррекцию за счет учета скорости движения колесной пары.

Если ограничиться изгибом в плоскости наибольшей жесткости, то динамическое поведение рельса может быть описано системой двух уравнений. Переходя к статической задаче (опуская силы инерции) можно привести эту систему к одному уравнению четвертого порядка.

Здесь Р – постоянная сила давления колеса на рельс, приложенная в начале координат подвижной системы.

Уравнение дает возможность учесть деформации сдвига при изгибе рельса. Пренебрегая сдвигами, получим известное уравнение по теории Эйлера-Бернулли [2, 102].

Отметим, что учет деформаций сдвига в полученном решении дает возможность уточнить прогибы. В главе 5 (табл. 5.3) приведены сравнительные данные о влиянии деформаций сдвига на величину прогибов рельса. Поправки растут с увеличение жесткости упругого основания и достигают 12%. Выражением будем пользоваться для определения прогибов в числовых примерах.

Напряжения, найденные с использованием выражений остаются на том же уровне, что и без учета сдвигов. Ввиду этого при определении напряжений будем использовать выражения для силовых факторов, вытекающие из уравнения; они приведены в учебнике [2].

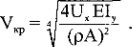
Рассмотрим теперь вопрос учета скорости движения поезда на напряженно-деформированное состояние рельса. Как показано в работе С.П. Тимошенко [109], динамический эффект движущейся с постоянной скоростью силы по балке (подразумевается модель Эйлера-Бернулли) на упругом основании аналогичен действию продольной сжимающей силы. Решая соответствующую задачу, можно получить выражение для прогиба балки под действием этой продольной силы при одновременном действии изгибающей силы Р. При определенном значении продольной силы наступает критическое состояние – балка выпучивается. На основании математической аналогии получается [109] такое выражение для критического значения скорости движения нагрузки (скорости поезда).

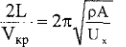
Физический смысл критической скорости состоит в том, что она является скоростью прохождения длины волны 2Ь, образующейся при изгибе рельса сосредоточенной силой Р, за время, равное периоду собственных колебаний рельса.

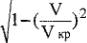
Определяемая выражением (18) критическая скорость оказывается на порядок больше реальной скорости движения поезда. При желании скорость движения нагрузки (поезда) можно учесть, если в выражения силовых и кинематических факторов ввести такой множитель.

Для практических расчетов этот множитель можно не учитывать. Далее в главе 5 в числовых примерах мы так и поступим.

Местные и контактные напряжения в сечении под колесом

В малой окрестности зоны контакта колеса с рельсом возникают местные напряжения. Экспериментальным путем эти напряжения были обнаружены С. Wilson [135]. Расчетным способом они могут быть определены на основании решения соответствующей задачи теории упругости. В работе С.П. Тимошенко [109] приведены теоретические результаты, которыми мы воспользуемся. В точке приложения сосредоточенной силы Р действует самоуравновешенная система двух сил, каждая из них равна — (рис. 1).

Эти дополнительные напряжения быстро затухают по мере удаления от точки приложения силы; также быстро затухают и основные напряжения.

Рассмотрим теперь вопрос о контактных напряжениях и о поперечном надавливании волокон в рельсе. Будем опираться при этом на теорию, изложенную А.Ф. Смирновым [102, стр. 184]. Выделим двумя бесконечно близкими поперечными сечениями элемент рельса. Затем проведем горизонтальное сечение на расстоянии х от начала координат. Касательное напряжение т может быть найдено по известной формуле через перерезывающую силу.

Зная напряжение, можно вычислить деформацию поперечного сжатия волокон. Для балки прямоугольного сечения b(x) = Const; напряжения в соответствии с формулой распределяются по закону кубической параболы. Для рельса, имеющего более сложное поперечное сечение, этот закон оказывается другим. В точке контакта на головке рельса получаем выражение для контактного напряжения.

Используемая Литература

• Смирнов А.Ф., Александров А.В. и др. Сопротивление материалов: Учеб. для вузов. – М.: Высшая школа, 1975. – 480 е.: с ил.
• Тимошенко С.П. Прочность и колебания элементов конструкций. -М.: Наука, 1975.-576 с.
• Wilson C. “Phil. Mag.”, vol. 32, 1891, p. 481.
• Бромберг Е.М., Вериго М.Ф., Данилов В.Н., Фриш- ман M. А. Взаимодействие пути и подвижного состава. М.: Трансжелдориз- дат, 1956. – 280 с.
• Александров A.B., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов. – М.: Высшая школа, 1995. – 560 е.: ил.
• Тимошенко С.П. К вопросу о вибрациях рельсов. Изв. электро- техн. ин-та, т. XIII, 1905. 17 с.
• Тимошенко С.П.О динамических напряжениях в рельсах // Вестник инженеров,-1915, -т. 1, N 4, – С. 143-152.
• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. Издание 4-е. -М.: Наука. Гл. ред. физ.-мат. лит.,1977.-832 с.