Численные алгоритмы расчетов

Оглавление

Цикл статей:

Глава 1 – Ударное взаимодействие колеса и рельса
Глава 2 – Исходные уравнения и характеристики
Глава 3 – Аналитические решения задач взаимодействия колеса и рельса
Глава 4 – Численные алгоритмы расчетов
Глава 5 – Результаты расчетов и сравнение с экспериментом

Обратное интегральное преобразование Лапласа при заданной форме импульса

Выражения для изображений искомых функций (z, s) и q> (z, s) представляют собой мероморфные функции. В общем случае оригиналы – искомые функции t) и (p(z, t) – не могут быть записаны в удобной аналитической форме и обращение приходится выполнять численно.

Для численного обращения преобразования Лапласа используются различные подходы [57, 71, 115]. Применим алгоритм, основанный на разложении оригиналов в ряд Фурье на некотором интервале времени Т. Неизвестный оригинал, действительно значная функция действительного переменного, в общем случае выражается через известное изображение F(s) – комплексно значную функцию комплексного переменного так.

Заметим, что значение изображения силы в нуле равно импульсу силы (оригинала), т.е. определенному интегралу от оригинала по времени.Алгоритм был проверен на решении большого числа тестовых примеров при трех различных формах ударного импульса.

Импульс прямоугольной формы.

Здесь Р₀ – максимальное значение силы, 1;₀ – продолжительность ее действия. При решении тестовых примеров сравнивалось поведение трех различных моделей балок (Тимошенко, Рэлея, Эйлера) от указанных воздействий.

Проведенные расчеты выявили такие условия: период Т при обращении

изображения ударной силы Р^) следует брать равным (2п+1)^, а при обращении изображения перемещений частота бесконечного спектра модели балки, ниже которой волновых процессов не происходит; п – целое положительное число.

Рекомендуется брать порядка 0.01 Ц ; число членов ряда не менее 100: -50 < к < 50 при рассмотрении небольших интервалов времени (порядка Ю1;₀) и не менее 600: -300 < к < 300 для интервалов времени порядка ЮО^. При выполнении этих условий относительная погрешность расчета не превышает 1%. Интересно, что при 1:₀ > 50 мс нагружение является квазистатическим. Численное обращение по описанному алгоритму выполняется достаточно быстро даже на персональных компьютерах с 386-м процессором.

Решение линеаризованного уравнения удара с использованием численного обращения преобразования Лапласа

В выражение входит С – приведенная контактная жесткость, зависящая от максимума оригинала силы и контактной жесткости (2.24), и для ее определения приходится проводить следующий итерационный процесс: на первом шаге задаемся некоторым априорным “значением максимума силы, вычисляем по нему С и получаем изображение P(s) по (4.2). Затем, переходя к оригиналу P(t) по описанному алгоритму, получаем его максимальное значение, которое опять подставляем в выражение для С и повторяем все сначала. Этот процесс сходится к некоторому значению С, в результате чего получаем искомый оригинал силы P(t).

Следует отметить, что при произвольном значении С величина Р(0) не равна нулю и может быть даже отрицательной. В ходе итерационного процесса, когда получаемый шагами по t положительный оригинал P(t) становится отрицательным, что противоречит смыслу задачи, это значение t=t₀ считается длительностью удара. При t > t₀ контактная сила Р принудительно обнуляется. Поэтому полученная функция не соответствует оригиналу от (4.2).Для определения силовых и кинематических факторов удара по формулам параграфа 3.2. нужно изображение контактной силы Р. В силу специфики алгоритма изображение контактной силы вычисляется лишь в конечном числе точек s_k=ik(D. Поэтому окончательно полученную функцию P(t) переводим прямым преобразованием Лапласа по t в изображения.

Из проведенных многочисленных расчетов ударного процесса по этому

алгоритму следуют условия: N > 70 (на практике N « 100), At« 0.011₀ (шаг по времени при определении P(t) и численном взятии интегралов (4.3) прямого преобразования Лапласа). По формуле (4.4) находим искомые оригиналы кинематических и силовых факторов при ударе.

Расчеты показывают, что результаты существенно зависят от Т. Действительно, при обращении по (4.1) знаменатель (4.2) на определенных значениях Т обращается в нуль, при этом изображение силы и максимум ее оригинала устремляются к бесконечности. На этих значениях Т итерационный процесс по приведенной жесткости С расходится. Однако существуют значения Т, при которых максимум оригинала силы достигает некоторых минимальных значений и итерационный процесс сходится с малым числом итераций. Это видно из рисунка 4.1.

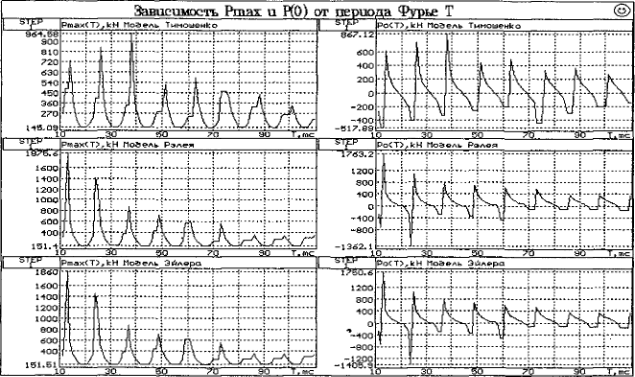
Рис. 4.1. Иллюстрация к численному алгоритму

Такое значение Т необходимо определить в начале алгоритма. Чтобы его найти, Т пробегает некоторый интервал за пределами зоны рассмотрения ударного процесса, на каждом шаге по Т выполняется вышеупомянутый итерационный процесс по С. Оптимальный период Т находится из условия тт{Ртах(Т)}. Затем в окрестности полученного значения Т происходит его коррекция по заданному начальному условию Р(0)=0 методом дихотомии. Здесь на каждом шаге также приходится выполнять итерационный процесс по С. В результате получаем окончательную Р(Т), и поступаем так, как описано выше – отсекаем отрицательные значения, численно выполняем прямое преобразование Лапласа для Р(Т), используя формулу (4.5), находим искомые функции.

В случае повторных ударов (например, двойного удара колеса с наваром), решаем задачу отдельно для каждого удара (пробегая по Т и С), полученные значения Р;(Ч), складываем, учитывая время начала каждого удара относительно предыдущего, выполняем над суммарной функцией Р(Х) численное прямое преобразование Лапласа и далее действуем, как было описано выше.Спектральные плотности [64] вычисляются после определения периода Фурье Т. Для этого используется тот же алгоритм прямого преобразования Лапласа по (4.3, 4.4), только к=1, а со пробегает некоторый интервал. Спектральная плотность вычисляется по такой формуле.

Решение нелинейного уравнения удара методом Эйлера на основе аналитических выражений реакции рельса

Уравнение (5) можно решать и в нелинейной форме методом Эйлера [3, 54], если возможно построить аналитические выражения для ^(Р^) . Это удается выполнить для модели Эйлера при 2=0, используя представление функций Бесселя в виде определенных интегралов или степенных рядов [103].

В этом случае нелинейное уравнение удара (2.23) решается с учетом аналитических выражений для £,(Р,10 методом Эйлера: на первом шаге Р(0)=0 подставляется в правую часть, численно находятся определенные интегралы с вышеупомянутыми функциями Бесселя, в левой части уравнения находится Р(Д1;), затем она подставляется в правую часть, а в левой таким же образом находится Р(2А1) и т.д. до конца рассматриваемого интервала. Затем, используя аналитические выражения для С), М численным интегрированием получаем искомые кинематические и силовые факторы ударного процесса.

Краткое описание программного комплекса

Специально разработанное программное обеспечение написано на языке С++ и состоит из основного блока программ для реализации изложенных численных алгоритмов, а также дополнительных программ. Все программы работают в среде DOS, исполняемый модуль оптимизирован по быстродействию и обработан упаковщиком ехе-файлов LZEXE. В табл. 4.1. приведены краткие характеристики программных продуктов.

Основной блок IMPACT реализует алгоритмы, описанные в п. 4.2. Он включает в себя ряд этапов:

вычисление начальной скорости удара для различных видов дефектов,
определение силовых и кинематических параметров ударного процесса, как функций времени;
зависимости максимумов параметров от продольной координаты,
расчет спектральных плотностей параметров удара,
вывод результатов в файл.

На всех этапах используются операции комплексной алгебры. Всего для блока IMPACT автором написано 23 подпрограммы (исключая стандартные [11, 95]). Программа снабжена диалоговым меню, позволяющим выбирать различные варианты расчета. Во время работы основные параметры расчета отображаются на экране, что позволяет следить за ходом процесса. Исходные параметры программа читает из отдельного текстового файла, поэтому они могут быть легко изменены. Комплекс занимает менее 30 Кбайт дисковой памяти вместе с файлами параметров. Быстродействие позволяет ему работать даже на ПК с 386-м процессором (расчет параметров во времени или спектральных плотностей длится менее одной минуты, а на современных ПК – несколько секунд).

Описанный комплекс позволяет решать задачи удара для колеса с ползуном (учитывая сглаживание хорды) или наваром, для удара на стыке, рассчитывать повторные удары.

К расчетному комплексу IMPACT прилагается комплекс READER, предназначенный для вывода на экран получаемых расчетным или экспериментальным путем массивов данных. При этом на экран могут быть выведены результаты в произвольном числе окон, можно производить различные операции (n-кратное дифференцирование или интегрирование, сдвиг и масштабирование аргумента и функции, запись в файл).

Этот комплекс использует графические средства С++ [11, 97, 121]; в нем стандартные драйверы и различные графические шрифты включены в главный модуль, вместе с текстовым файлом параметров занимающий менее 50 Кбайт дискового пространства.

Программа IMPVAR представляет собой измененный вариант программы IMPACT, рассчитанный на получение зависимостей максимальных значений параметров ударного процесса при изменении характеристик U_x, V₀, К₀, At, N.

Дополнительные программы составлены для определения исходных параметров (V₀, Kq, I_d). Программа V0 по заданным значениям нагрузки на колесо, параметров колеса и дефектов на нем вычисляет начальную скорость соударения колеса и рельса V₀ в зависимости от скорости движения поезда.Программа CONTACT вычисляет значение контактной жесткости в соответствии с выражением (2.40), численно находя при этом полные эллиптические интегралы 1 -го и 2-го рода через подпрограмму, использующую их полиномиальное приближение [103].

Программа ID вычисляет геометрическую крутильную жесткость рельса I_dпо различным вариантам разбиения сечения, с учетом и без учета поправок Феппля, находит средние значения от полученных величин.

Все программы, составленные на С++, читают исходные данные расчета из текстового файла, который имеет удобную и понятную структуру и снабжен комментариями. Это позволяет легко и быстро вносить любые изменения в блок исходных параметров.

Разработанное программное обеспечение обладает достаточной универсальностью, позволяя варьировать в широких пределах исходные данные и характеристики рассматриваемой системы, имеет достаточное быстродействие.

Таблица 4.1.Название	Язык	Основное назначение программы
IMPACT(комплекс)	С++	Расчет силовых и кинематических характеристик рельса при ударе во времени, их максимальных значений по продольной оси рельса с выбором модели рельса. Расчет спектральных плотностей
IMPVAR(комплекс)	С++	Получение зависимостей максимальных значений параметров ударного процесса при изменении характеристик и_х, У₀, Ко, N (число членов ряда)
IMPFUR	С++	Определение зависимостей Р_тах(Т), Р₀(Т)
COMPARE	С++	Расчет балок по различным моделям на заданную силу Р(1;) – тестовые примеры
READER(комплекс)	С++	Вывод на экран результатов расчета или натурных измерений в наглядной графической форме
LOADRAIL	BASIC	Вычисление параметров напряженно-деформированного состояния рельса по известным силовым и кинематическим характеристикам при качении колесной пары с дефектами и с учетом местных напряжений и деформаций
V0	С++	Вычисление начальной скорости соударения, предельной скорости движения поезда
CONTACT	С++	Определение параметра контактной жесткости соударяющихся тел (с численным нахождением эллиптических интегралов)
ID	С++	Вычисление геометрической жесткости рельса при кручении

Используемая Литература

Справочник по специальным функциям с формулами, графиками и таблицами. Под ред. М. Абрамовича и И. Стиган. – М.: Наука, 1979. – 832 с.
Шикин А.В., Борее ко в А.В. Компьютерная графика. Динамика, реалистические изображения. – М.: ДИАЛОГ-МИФИ, 1998. – 288 с.
Прокофьев Б.П., Сухарев Н.Н., Храмов Ю.Е. Графические средства Turbo С и Turbo С++ / Под. ред. Г.В. Генса, Ю.Е. Храмова. – М.: Финансы и статистика, СП ” Ланит”, 1992. – 160 с.
Белецкий Я. Энциклопедия языка Си: Пер. с польск. – М.: Мир, 1992.-687 е.: ил.
Подбельский В.В. Язык Си++: Учеб. пособие. – 3-е изд., дораб. – М.: Финансы и статистика, 1998. – 560 е.: ил.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. Издание 4-е. -М.: Наука. Гл. ред. физ.-мат. лит.,1977.-832 с.
Амосов A.A., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Учеб. пособие. – М.: Высшая школа, 1994. – 544 е.: ил.
Крылов В.И., Скобля Н.С. Методы приближенного преобразования Фурье и обращения преобразования Лапласа. Справочная книга. – М.: Наука, 1974. – 224 с.
Ланцош К. Практические методы прикладного анализа. Справочное руководство. Пер. с англ. Под. ред. A.M. Лопшица. М., 1961. – 524 с.
Хемминг Р.В. Численные методы. Для научных работников и инженеров. Изд. 2-е, испр. М.: Наука, 1972. – 400 с.