Цикл статей:
Глава 1 — Ударное взаимодействие колеса и рельса
Глава 2 — Исходные уравнения и характеристики
Глава 3 — Аналитические решения задач взаимодействия колеса и рельса
Глава 4 — Численные алгоритмы расчетов
Глава 5 — Результаты расчетов и сравнение с экспериментом
Динамические уравнения моно симметричного стержня на упругом основании
Рельсовый путь, находящийся на линейно-упругом основании, подвержен действию подвижной нагрузки. В общем случае нагрузка действует как в плоскости наибольшей жесткости рельса, так и в плоскости наименьшей жесткости. При этом в поперечных сечениях возникают также крутящие моменты. Поэтому для полного описания динамического поведения рельса следует привлечь теорию, в которой учитываются все компоненты напряженно- деформированного состояния.
По своему характеру рельс занимает некоторое промежуточное положение между стержнями сплошного сечения и тонкостенными стержнями открытого профиля (см. рис. в «ПРИЛОЖЕНИИ» на стр. 62). Основное отличие тонкостенных стержней — существенное влияние депланации поперечных сечений. Поперечное сечение рельса имеет одну плоскость симметрии; основной вклад в развитие депланаций вносят стенка с подошвой.С учетом вышесказанного можно поведение рельса как балки (стержня) описать системой шести дифференциальных уравнений в частных производных второго порядка [79]. С учетом реакции упругого линейно-деформируемого основания и сосредоточенной силы, приложенной в сечении г=0.
Перемещения центра изгиба поперечного сечения стержня по направлениям главных осей и угол закручивания сечения вокруг линии центров изгиба, Фу,(рх,срю— Углы поворота поперечного сечения вокруг главных осей и мера депланации сечения, 1у,1х,1ю — Главные осевые и секториальный моменты инерции, — Момент инерции при кручении, ах — Расстояние от центра тяжести до центра изгиба.
Уравнения описывают динамический изгиб рельса в плоскости наибольшей жесткости; они независимы от остальных уравнений. Уравнения представляют собой связанную систему уравнений, описывающих динамику изгиба в плоскости наименьшей жесткости, сопровождающегося закручиванием рельса.
Система учитывает деформации сдвига. Углы сдвига в главных плоскостях рельса, неявно присутствующие в уравнениях.
Если переписать их в другом виде, то становится более ясным геометрический смысл соотношений: полные углы наклона касательной к упругой кривой оси центров изгиба сечений складываются из углов сдвига и углов поворота сечений. Эта истина известна, она изложена в книге [108] С.П. Тимошенко, которому принадлежит приоритет в создании динамической модели изгиба балки (стержня) с учетом деформаций сдвига. Система уравнений для стержня, не имеющего плоскостей симметрии, она приведена в работах [74 — 76], распространяет динамическую модель С.П. Тимошенко на пространственное изгибно-крутильное движение стержня (балки). Ввиду этого далее для краткости мы будем называть уравнения моделью Тимошенко.
Геометрический параметр у а имеет ту же размерность (м»1) , что и мера депланации фт. Ввиду этого его можно назвать — мера дополнительной депланации, возникающей за счет учета деформаций сдвига; параметр у а является аналогом углов сдвига при изгибе и проявляется при стесненном кручении стержня (в нашем случае — рельса).
Из системы уравнений могут быть получены за счет пренебрежения теми или иными факторами уравнения для других моделей (В.З. Власова [30, 31], Релея, Бернулли-Эйлера). Они обсуждаются далее в параграфе 2.2. Коэффициенты формы поперечного сечения стержня возникают в дифференциальных уравнениях при учете деформаций сдвига.
Следует заметить, что по сравнению с приведенными в статье [79] выражениями ку для коэффициентов формы поперечного сечения здесь даются обратные величины. Для ориентировки читателя приведем известное из учебников по сопротивлению материалов [2, 102] значение коэффициента формы сечения для стержня (бруса) прямоугольного очертания (при плоском изгибе).
На кафедре теоретической механики МИИТа имеется программа для вычисления геометрических характеристик, а также таблицы результатов. В приложении приведены числовые значения всех необходимых геометрических характеристик поперечного сечения для четырех типов рельсов.
Динамические уравнения, соответствующие классическими приближенным моделям
Для перехода от уравнений модели Тимошенко к классическим моделям систему уравнений можно свести к трем уравнениям, исключив углы сдвига.
В классической теории В.З. Власова [30] не учитываются деформации сдвига. Поэтому все коэффициенты формы обращаются в нули: ^ = 0, а вместо соотношений (8) и (9) между обобщенными перемещениям будет соблюдаться известная более простая зависимость.
Используя выражения, можно перейти от уравнений к описанию динамического поведения рельса на упругом основании в соответствии с теорией В.З.Власова [30].
Уравнение описывает движение рельса в плоскости симметрии, являющейся плоскостью наибольшей жесткости. Оно отвечает модели Релея, поскольку в нем учитывается инерция поворота сечения. Уравнения совместно описывают изгибно-крутильное движение рельса. Эти уравнения В.З. Власова распространяют модель Релея на пространственную задачу. Далее будем называть эти уравнения моделью Релея-Власова. Если пренебречь в уравнении инерцией поворота, то мы получим уравнение, соответствующее модели Эйлера-Бернулли.
Кроме традиционных моделей, ставшими уже классическими, иногда для практических оценочных расчетов используются приближенные модели. В работе [77] предложены две такие модели. Одна опирается на результаты асимптотического анализа решения по модели С.П. Тимошенко, полученного с помощью преобразования Лапласа; вторая имеет итерационный характер. Применительно к рассматриваемой задаче в случае плоского изгиба итерационный подход выглядит следующим образом. На первом шаге итерации в уравнении опускается слагаемое, содержащие угол поворота сечения.
Построив решение £,Х(Р) на основё этого уравнения, на втором шаге итерации его используют для определения угла поворота фу из такого уравнения:
Уравнениями приближенно описывается динамическое поведение стержня при коротких ударных воздействиях. В работах В.Б. Мещерякова с сотрудниками [78, 80, 81] оценки напряженно-деформированного состояния рельса при ударе получены с помощью описанного приближенного подхода. Недостаточная точность решений компенсируется наличием аналитических выражений для силовых и кинематических факторов, характеризующих ударный процесс. Численный метод в этом случае требуется применять только для решения нелинейного интегрального уравнения.
Интегральное уравнение удара по теории Герца и его возможная линеаризация
Поведение взаимодействующих тел будем рассматривать в подвижной системе координат. Скорость движения системы координат равна скорости вагона (поезда); начало отсчета продольной координаты ъ лежит в поперечном сечении рельса, которое находится под точкой контакта с колесом. При ударе в точке контакта возникает сила, от которой зависит напряженно- деформированное состояние взаимодействующих тел.
Достаточно полный анализ напряжений при контакте двух упругих тел был впервые выполнен в 1882 году Г. Герцем [125]. Как отмечается в монографии К. Джонсона [41], развитие теории Герца стало стимулироваться в начале нашего века, в частности, техническими достижениями в железнодорожном транспорте. Допущения теории Герца могут быть сформулированы следующим образом:
- Поверхности контактирующих тел гладкие и несогласованные, т.е. характерный размер области контакта значительно меньше относительного радиуса кривизны контактирующих поверхностей.
- Деформации в зоне контакта малы.
- Каждое из контактирующих тел может рассматриваться как упругое полупространство.
- Трение по поверхности контакта отсутствует.
Выполним количественную оценку применимости теории Герца к поставленной задаче, используя расчетные выражения из монографии К. Джонсона [41, стр.109]. Предварительные расчеты при скорости движения поезда 80 км/час дают для полной нагрузки при ударном взаимодействии величину порядка Р=320000 Н.
Принимая относительный радиус кривизны Я0 равным 0.271 м, а приведенный модуль упругости Е,=0.546Е (где Е — модуль упругости стали), получаем гк=0.0083 м. Отношение гк/Я=0.0083/0.271=0.03, следовательно, первое допущение выполняется. Найдем теперь относительное сближение удаленных точек двух тел:
X = £ = 0,00025 м
Второе допущение также выполняется, так как это сближение значительно меньше характерных размеров сечения рельса. Третье и четвертое допущения остаются теми гипотезами, справедливость которых может быть подтверждена при сопоставлении результатов расчета с данными эксперимента.
Таким образом, контактная сила Р(Ч)л может быть определена из решения нелинейного интегрального уравнения в соответствии с теорией Г. Герца [36, 125]. В основу составления этого уравнения кладется такое соотношение.
Здесь К^ — параметр контактной жесткости, зависящий от геометрии зоны контакта и материала соударяющихся тел [36, 41, 45]; ик— вертикальное перемещение колеса в точке контакта. Если принимать во внимание только местные упругие деформации колеса, то ик можно выразить в таком виде.
Вертикальное (точнее сказать — в плоскости наибольшей жесткости)перемещение рельса иг равно перемещению У*) центра изгиба Б поперечного сечения рельса по направлению главной оси. Это перемещение далее мы будем получать на основе использования различных динамических моделей для рельса.
Уравнение можно линеаризовать, заменяя нелинейность в левой части на Рф/С, где С — приведенная жесткость эквивалентной пружины, определяемая по критерию равенства энергии местных деформаций.
Здесь Ртах — априорно задаваемый максимум ударной силы. Его величину можно уточнять итерациями.
Начальная скорость удара по рельсу колеса с ползуном
Вспомогательной задачей, возникающей при исследовании ударного взаимодействия колеса и рельса, является задача об определении начальной скорости их соударения (назовем ее У0). Ее важность состоит в том, что величина скорости соударения входит в уравнение удара и существенно влияет на решение.
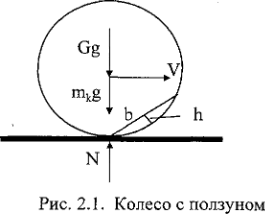
Рассмотрим некоторые особенности движения колеса с дефектом. В тот момент времени, когда колесо касается рельса точкой начала хорды Ь ползуна, качение колеса прекращается и центр колеса начинает двигаться по дуге окружности (рис.1). У центра колеса появляется нормальное ускорение (при движении по прямолинейной траектории это ускорение отсутствует).Если записать теорему о движении центра масс колеса в проекции на нормаль, то можно получить выражение для предельного значения скорости вагона, при котором реакция рельса N (численно равная давлению) обращается в нуль.
Здесь введены такие обозначения: шк — масса колеса, Я — радиус колеса, V — скорость поезда, § — ускорение свободного падения, в — масса полезного груза, приходящегося на одно колесо, ¡и — динамический коэффициент (от вибрации вагона).
Вычислим начальную скорость У0 ударного взаимодействия колеса с рельсом, используя две различные модели. Скорость поезда V будем считать неизменной во времени.
Условие удара представляет собой равенство нулю суммарного вертикального перемещения:
Н(1)= Н, — н2(1) — Н3(1)=0 (2.31)
Начальная скорость удара по рельсу колеса с наваром
Кроме довольно распространенного дефекта на колесных парах — ползуна — встречается так называемый навар. Это небольшое утолщение на ободе колеса; мы моделируем его очерченным дугой окружности с радиусом, равным удвоенному значению величины выступа (рис. 3). При наличии навара происходит обязательно два удара.
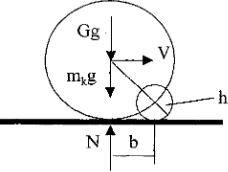
Рис. 2.3. Колесо с наваром
Как видно из рис. 2.3, роль хорды ползуна теперь играет отрезок общей касательной к окружностям колеса и навара. Что касается второго удара. то на него распространяется понятие предельной скорости, и в случае У>V используется такое выражение.
Контактная жесткость в точке удара
Параметр контактной жесткости К0 , входящий в нелинейное интегральное уравнение удара (2.23) определяет зависимость между контактной силой и взаимным сближением двух тел. Контактная жесткость зависит от материала и геометрии тел в зоне контакта. Определять ее можно как теоретически, так и по
данным испытаний. Для теоретического определения воспользуемся подходом Г. Герца для нормального контакта упругих тел [36, 41]. Опишем контактирующие поверхности в окрестности зоны контакта уравнениями второго порядка и определим для каждой главные радиусы кривизны в точке контакта (Яц, Я12 для первой поверхности и Я21 Д22 для второй). Предположим, что область контакта имеет форму эллипса с полуосями а и Ь, Ъ < а и эксцентриситетом е = л/1 — Ь2 / а2 . Следуя Герцу, используем аналогию с соответствующей задачей электростатического потенциала. Имеем такое распределение давления по данной эллиптической области при действии силы Р.
Понятно, что длины полуосей а и Ъ зависят от контактной силы и геометрии тел в области контакта. Однако для определения контактной жесткости требуется лишь их отношение, которое в случае а/Ь < 4 (не слишком вытянутый эллипс) приближенно можно вычислить по формуле.
При контакте рельса и колеса без дефектов или с дефектом в виде навара контактная жесткость вычисляется по формуле (40) с учетом (41). В случае контакта рельса и колеса с ползуном, который можно представить плоской площадкой эллиптического очертания, в формуле (40) будет только один конечный радиус кривизны — радиус головки рельса, а отношение Ь/а можно вычислить явно.
В таблице 2.1 приведены результаты расчетов контактной жесткости. Для получения этих числовых результатов была составлена и отлажена специальная программа. Полные эллиптические интегралы вычислялись через полиномиальное приближение [103].
Значения контактной жесткости
| Тип | Профиль колеса | Профиль с | Профиль с | Имитация | |
| рельса | Новый | Изношенный | ползуном | наваром | шарами |
| Р43 | 9.04-Ю10 | 1.55-1011 | 1.15-1011 | 7.59-Ю10 | 6.28-Ю10 |
| Р50, Р65, Р75 | 1.02-1011 | 2.41-1011 | 1.47-1011 | 8.7М010 | 7.23-Ю10 |
Крутильная жесткость рельса
При рассмотрении задачи изгибно-крутильного движения рельса используется понятие крутильной жесткости, под которой понимается произведение модуля сдвига в на геометрическую характеристику [6, 98].
Функция напряжений и(х, у) (функция Прандтля) определена в области поперечного сечения и является решением уравнения Пуассона: Ди=-2 (А — оператор Лапласа). Геометрическую жесткость можно также вычислять через функцию кручения Сен-Венана ср(х, у) (функцию перемещения). По определению ее произведение на угол закручивания представляет собой перемещение вдоль продольной оси.
Многие исследователи занимались определением крутильной жесткости [94, 98]. В табл. 1 приведены некоторые результаты. Геометрическую жесткость балки с достаточно сложным сечением, какой является рельс, будем искать в первом приближении: разобьем сечение рельса на простейшие фигуры с известной жесткостью и просуммируем их, полагая, что при этом сохраняется достаточная точность искомой величины. При этом, следуя Фепплю, используем поправочные коэффициенты а. Вычислив жесткости по различным вариантам разбиения (рис. 4), найдем среднее значение для данного типа рельса (Р50, Р65, Р75). В таблицах 2 и 3 приведены результаты этих расчетов.
Приближенные формулы для простейших фигур
| Виды поперечных Сечений | Формулы для вычисления геометрической Жесткости 1(1 простейших фигур |
| Эллипс | тса Ь ,— , а,Ь — большая и малая полуосиа +Ь |
| Прямоугольник | О *каЬ , а,Ь — большая и малая стороны, |
| Прямоугольник узкий | аЬ3 / 3, а, Ь — большая и малая стороны |
| Трапеция | Ь, с^, с12 — высота и стороны |
| Тавр (по Веберу) | с13 (а + Ь — 0.9с!) / 3, с!, а, Ь — толщина полок и стенки (одинаковая), высота, длина |
Таблица 2.3.
Значения геометрической жесткости (см4)
| Схема разбивки | °50 | Р65 | Р75 | |||
| <х=1 | а=1.15 | а=1 | а=1.15 | а=1 | а=1.15 | |
| 1 | 132 | 138 | 185 | 196 | 290 | 304 |
| 2 | 134 | 140 | 182 | 192 | 287 | 303 |
| 3 | 134 | 140 | 185 | 195 | 290 | 304 |
| 4 | 110 | 116 | 157 | 167 | 248 | 261 |
| 5 | 117 | 123 | 161 | 171 | 258 | 273 |
| 6 | 117 | 123 | 164 | 175 | 259 | 274 |
Таблица 2.4.
Средние значения геометрической жесткости
| Типы рельсов | Р50 | Р65 | Р75 |
| I, (см4) | 126 | 177 | 279 |
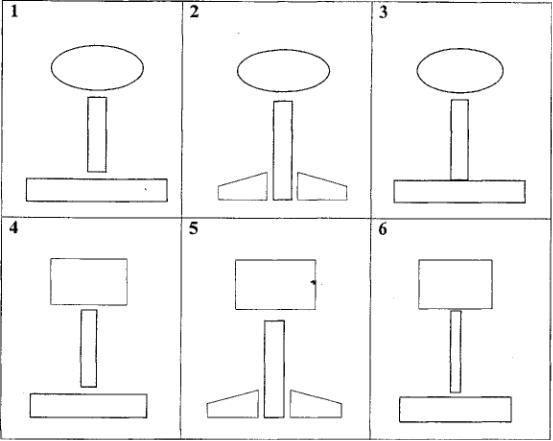
Рис. 2.4. Схемы разбиения поперечного сечения рельса
Жесткость упругого основания
Гипотезу о линейной зависимости между осадкой основания и его реакцией ввел в обиход Н.И. Фусс в 1801 г. [110]. В применении к балкам на упругом основании она была широко использована в работах Е. Винклера. В 1867 г. им было издано руководство по сопротивлению материалов, где впервые была поставлена задача об изгибе балок на упругом основании. Там же была отмечена применимость этой теории к вычислению напряжений в железнодорожном пути [110].
Относительно названия характеристик упругого основания в научной литературе нет единого мнения. Так, например, в книге Т. Пешля [94] речь идет о коэффициенте постели (с размерностью Н/м3) или о погонном коэффициенте постели (с размерностью Н/м2). В современном учебнике по сопротивлению материалов [2] при выводе дифференциального уравнения изгиба балки на упругом основании также используется понятие коэффициента постели. Умножая его на ширину балки, тем самым вводится погонный коэффициент постели.
В монографии ведущих специалистов по взаимодействию пути и подвижного состава [27] обсуждаются такие понятия: вертикальная жесткость пути (с размерностью Н/м), вертикальная погонная жесткость основания (с размерностью Н/м2). Последняя может называться также физическим модулем упругости пути. Здесь же отмечено, что этот модуль имеет различные значения для различных конструкций пути. В книге Н.Д. Кравченко [55] используются понятия: вертикальная и горизонтальная жесткость пути (с размерностью Н/м).
Что касается количественных данных, характеризующих жесткость упругого основания, то нет (и не может быть) однозначных ответов. Дело заключается в том, что эти данные существенно зависят от конструкции верхнего строения пути и от его текущего состояния. В книгах [27] и [55] отмечается, что вклад составных частей верхнего строения пути в формирование жесткости пути различается в зависимости от их собственных характеристик. Для летних и зимних условий жесткость основания может отличаться в 2-3 раза. При этом важно учитывать тип рельсов и шпал, промежуточных скреплений. Как следует из сказанного, достоверные сведения о параметрах жесткости основания могут быть получены только экспериментальным путем. На эти эксперименты многими коллективами были затрачены годы кропотливой работы [27, 55].
В нашем теоретическом исследовании исходные дифференциальные уравнения (1-6) содержат характеристики жесткости упругого основания их,иу,ию, существенно влияющие на решение рассматриваемой задачи. Будем называть их жесткостью основания, причем отметим их размерности: [ихмиу]= Н/м2, [Щ=Н. Количественные данные при решении иллюстрационных примеров будем задавать как известные исходные данные, в широком диапазоне значений.
При сравнении результатов расчета с экспериментальными данными можно поступать двумя способами. Первый способ, в рамках диссертации для нас недоступный, состоит в том, что жесткость основания должна быть определена специально поставленным экспериментом для данных условий. Тогда
* .сопоставление расчета и эксперимента позволит судить о точности расчета. Второй способ заключается в том, что сопоставление расчетных и экспериментальных данных является косвенным экспериментом и позволяет уточнять параметры жесткости основания. Этим мы и воспользуемся в пятой главе.
Используемая Литература
- Вериго М.Ф., Коган А.Я. Взаимодействие пути и подвижного состава. М.: Транспорт, 1986. — 559 с.
- Кравченко Н.Д. Новые конструкции железнодорожного пути для метрополитенов. М.: Транспорт, 1994. 143 с.
- Пешль Т. Сопротивление материалов. M.-JI. ОГИЗ, 1948. — 250 с.
- Александров A.B., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов. — М.: Высшая школа, 1995. — 560 е.: ил.
- Арутюнян Н.Х, Абрамян Б. Л. Кручение упругих тел. М., Физ- матгиз, 1963. — 610 с.
- Прочность. Устойчивость. Колебания. Справочник в 3-х томах. Том 1. Под. ред. И.А. Биргера и Я.Г. Пановко. М.: Машиностр., 1968. — 831 с.
- Справочник по специальным функциям с формулами, графиками и таблицами. Под ред. М. Абрамовича и И. Стиган. — М.: Наука, 1979. — 832 с.
- Дженкинс Х.Х., Стефенсон Д.Е., Клейтон Г.А. Мор- ланд Г.В., Лайон Д. Влияние параметров пути на вертикальные динамические силы взаимодействия колеса и рельса.// Железные дороги мира.-1974, — N 11, — с.14-31.
- Джонсон К. Механика контактного взаимодействия . М.: Мир, 1989. 510 с.
- Зегжда С.А. Соударение упругих тел. — Спб: Издательство С.-
- Гольдсмит В. Удар. Теория и физические свойства соударяющихся тел. — М.: Стройиздат, 1965. — 447 с.
- Hertz H. Uber die Beruhrung fester elastisher Korper (On the contact of the elastic solids). -J. reine und angewandte Mathematik, 1882, B.92, S. 156-171.
- Мещеряков В.Б., Шимановский А.О., Исаев В.И. Приближенные модели для определения реакции балки на действие кратковременной сосредоточенной силы / Межвуз. темат. сб. тр. ЛИСИ: «Исследования по механике строительных конструкций и материалов». Л.: 1990. с.71…76.
- Мещеряков В.Б., Исаев В.И., Емельянова Г.А. Ударное взаимодействие рельсового пути и колесной пары, имеющей ползуны. Тезисы доклада на 8-ой Международной конференции «Проблемы механики железнодорожного транспорта». Днепропетровск, 1992 г. с. 62-63.
- Власов В.З. Тонкостенные упругие стержни. М., Физматгиз, 1959. 568 с.
- Ахметзянов М.Х., Тихомиров В.М., Шабанов А.П. Исследование напряженного состояния вагонного колеса и рельса // Экспериментальные и расчетные методы строительной механики. Сб. науч. тр. Новосибирск, СГАПС, 1997. с. 11-18.
- Багреев В.В. Протекание процесса удара за пределами применимости теории Герца. Инженерный журнал АН СССР. Том V. Выпуск 4, 1965.
- Смирнов А.Ф., Александров А.В. и др. Сопротивление материалов: Учеб. для вузов. — М.: Высшая школа, 1975. — 480 е.: с ил.
- Мещеряков В.Б., Исаев В.И., Емельянова Г.А. О возможности уточнения уровня изгибных напряжений в рельсах при ударах колесных пар с ползунами// Вестник ВНИИЖТ. 1996. N4. С. 16…19.
- Мещеряков В.Б., Кравцева Е.И. К вопросу эффективности сглаживания хорды ползуна колесной пары. В докладах Международного симпозиума «Безопасность перевозочных процессов», Москва, 1996. С.41-44.