Комплексная математическая модель многозвенной механической системы тележка – буксовые поводки – буксовые узлы – гребни колесной пары – рельсовая колея

Оглавление

Toggle

Цикл статей:
Глава 1 – Повышение ресурса колесных пар локомотивов с тележками поводкового типа

Глава 2 – Причины и факторы изнашивания бандажей колес локомотивов

Глава 3 – Комплексная математическая модель многозвенной механической системы «тележка – буксовые поводки – буксовые узлы – гребни колесной пары – рельсовая колея

Глава 4 – Конструкторское и технологическое совершенствование буксового поводка

Глава 5 – Экспериментальные исследования шарниров буксовых поводков

Глава 6 – Технология и функционально-стоимостный анализ эффективности модернизации буксовых поводков

Задачи моделирования комплексной математической модели многозвенной механической системы «тележка – буксовые поводки – буксовые узлы – гребни колесной пары – рельсовая колея»

Создатели и эксплуатационники ТПС оказались в неожиданном, но типичном на сети дорог состоянии-обобщенного интенсивного износа колес. Апогей явления физического и технологического износа бандажей колес локомотивов пришелся на 1995-1998 гг. Проблема взаимодействия колеса и рельса до настоящего времени волнует в равной степени работников многих инфраструктур железнодорожного хозяйства, но больше всего локомотивного, вагонного и путевого. Следует заметить, что разные интересы и разный уровень понимания и знания аспектов комплексной проблемы «колесо – рельс» приводят к недоразумениям и неоправданным взаимным обвинениям в «научной недобросовестности» и принятых тех или иных «сомнительных» технических решений. Об этом свидетельствует дискуссия по проблеме «колесо – рельс» проведенная на страницах отраслевой газеты «Гудок» в 2003 году. Научному сообществу необходимо было дать достоверные пояснения возникшему явлению. Однако, не смотря на имеющееся огромное количество научно-технической литературы по проблеме «колесо – рельс» анализ показывает, что подходы исследователей к ней выражены некоторой спецификой их разноплановых целей и решаемых задач. Так, в работах: [25, 26, 46-51, 55, 80] – основное внимание уделено изучению процессов взаимодействия рельсовой колеи и колес вагонов; [27-29] – приведены результаты экспериментальных исследований напряженного состояния колес и рельсов, методом и средствами фотоупругости; [57, 64] – отмечены предположения о возможных влияниях конструктивных решений экипажной части на изнашивание гребней колес подвижного состава.

Систематизированные многочисленные эксплуатационные данные износа колес тягового подвижного состава в соответствии с рисунками 1.1-1.6, а также характерные неисправности узлов и соединений экипажной части в соответствии с рисунками 2.1-2.8, целенаправленный инженерно-логический анализ в соответствии с рисунком 1.7, позволяют конкретизировать слабые конструкции оборудования экипажной части, оказывающие непосредственное влияние на изнашивание гребней колес в первую очередь. Из общего перечня причин и факторов заслуживают научного внимания буксовые поводки как непосредственные связи бесчелюстной рамы тележки с буксовыми узлами КМБ. Находясь на стадии только очевидных неисправностей этих конструкций в соответствии с рисунками 2.1-2.8 необходимо определить математические обоснования и закономерности, описывающие процессы взаимодействия элементов системы.

Эксплуатационной практикой неоднократно доказано, что достоинства аналога не подтверждаются при работе в условиях железных дорог сети. Механический перенос конструктивных решений на новые условия эксплуатации и технологии изготовления неприемлем. Эта ситуация неминуемо приводит к необходимости обоснованного физического и математического моделирования при решении проблемных и нетривиальных задач. Моделирование позволяет существенно снизить затраты труда и материалов, сэкономить финансовые средства и ускорить устранение общесетевой проблемы.

Раскрытие механизма взаимодействия или изнашивания позволяет анализировать влияние факторов, подбирать более стойкие материалы и определять область их применения. В этой связи необходимо: разработать методику расчета соединений рамы тележки с буксовыми узлами, которые по своим возможностям будут лишены недостатков предыдущих; выявить основные зависимости между критериями долговечности шарниров и параметрами, характеризующими конструкцию, технологию, режимы и условия эксплуатации локомотивов. Однако на данный момент не разработана методика расчета буксовых поводков на долговечность работы в структуре экипажной части, а имеются лишь отдельные примерные виды расчетов обрезиненных шарниров. Подходы к разработке методики на основе фундаментальных положений теории состоят в том, чтобы необходимо сохранить допустимую меру преемственности ранее принятых параметров модельных решений узлов.

В основу комплексной математической модели кинематики звеньев «КМБ – рама тележки» положен метод замкнутых векторных контуров, предложенный профессором В.А. Зиновьевым [81, 82]. Метод замкнутых контуров позволяет установить численные зависимости между переменными параметрами буксовых поводков и положением оси колесной пары, в бесчелюстной раме тепловоза по обобщенным координатам, в горизонтальной и вертикальной плоскости. Одновременно с положением оси колесной пары позиционируются гребни колесной пары по отношению к рельсовой колее. Для решения поставленной задачи выполнено уточнение идеализированного положения звеньев элементов экипажной части в соответствии с рисунком 3.1, при несвободном движении КМБ в прямых участках рельсовой колеи. Положение оси и перемещение буксовых узлов в горизонтальной продольной плоскости зависит от относительных параметров длины поводков.

В основу метода положена многозвенная кинематическая структура, представленная системой векторных тождественных уравнений подчиняющихся условиям замкнутости, когда суммы проекций сторон многоугольника на оси прямоугольной системы координат равны нулю. Чтобы воспользоваться этим условием, необходимо задать векторные направления изменения параметров звеньев многоугольника.

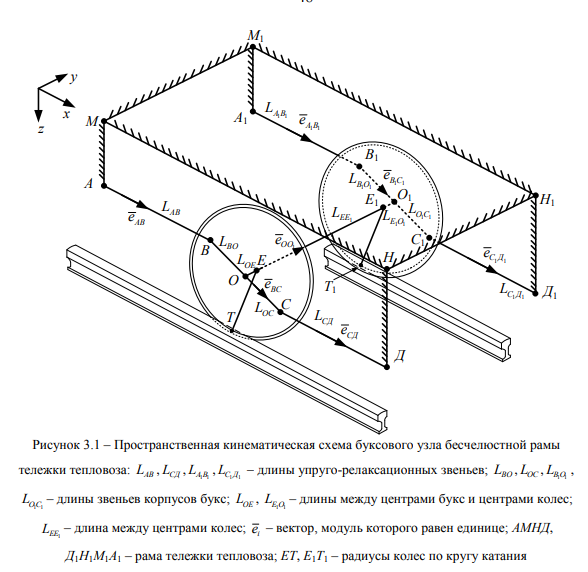
На идеализированной схеме кинематических контуров в соответствии с рисунком 3.1, можно видеть что:

• рама тележки, представлена схемой (АМНД.Д.Н.М.А.) и является абсолютно жестким звеном;
• вертикальные перемещения рамы и сопряжений (АД и АД.) буксовых поводков отсутствуют;
• буксовые сопряжения (ВС и В.С.) не имеют горизонтальных (по оси у) смещений;
• радиусы колес по кругу катания идентичны: ЕТ = Е.Т..

Система уравнений решается методом последовательных приближений (метод Ньютона). С применением электронных вычислительных машин, выполнено имитационное моделирование многозвенной механической структуры в дискретной форме (с точностью до 0,01 мм). Дискретные значения длины буксовых поводков, принимались в интервале (от 1 до 12 мм) по данным натурных измерений в процессе опытных поездок. Принимая дискретные значения обоснованного ряда длины буксовых поводков, определили: положения буксовых поводков в координатах х, у; количественные параметры перекоса осей в раме тележки; значения углов набегания гребней колес на боковые грани головок рельсов в прямых участках рельсовой колеи в соответствии с рисунком 3.2. Моделирование поведения механической системы выполнялось с соблюдением принципа Гамильтона, который состоит в том, что истинное положение звеньев системы (начальные и конечные состояния) находятся по заданным скалярным значениям.

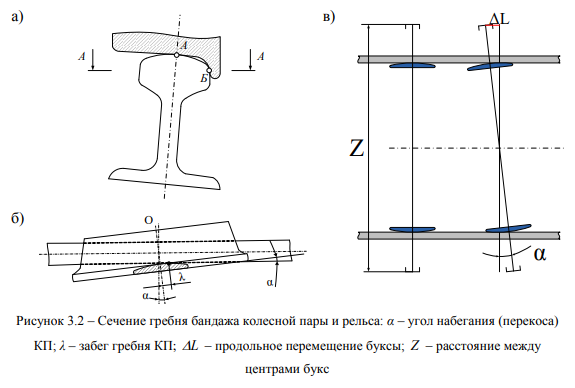
Функция, при этом не исследуется на определение минимума или максимума. Продольное перемещение буксы ЛЬ, в процессе имитационного моделирования (± 12 мм) выражено коэффициентом установки оси КП К_х. возможным ее перекосом в колее, как а = аго/.^ ^ ^^ в соответствии с рисунком 3.2, в.

Положение оси КП по отношению к продольной оси колеи и рамы тележки определяет значение угла набегания гребня на боковую грань головки рельса а (рисунок 3.2, б). Сечение гребня выполнено горизонтальной секущей плоскостью А -А параллельно поверхности головки рельса по поверхности катания бандажа в соответствии с рисунком 3.2, а.

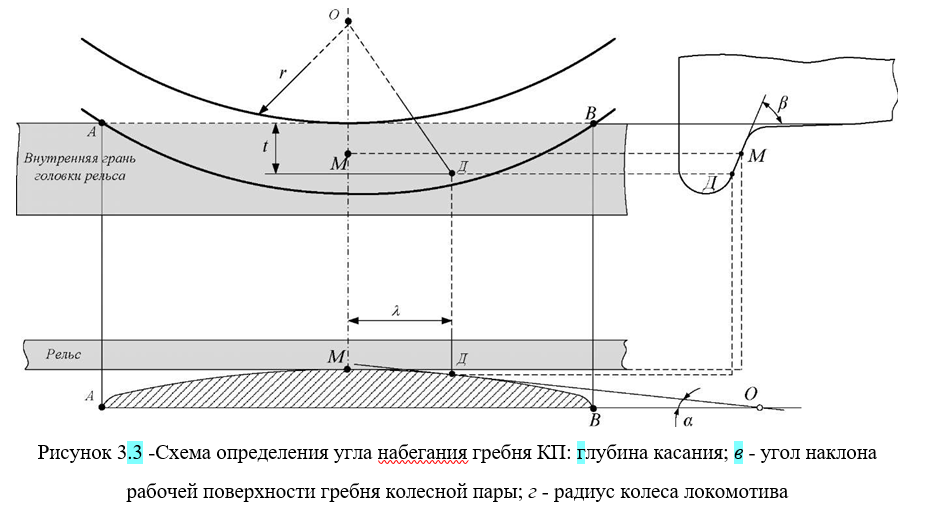
Для колесной пары диаметром 1050 мм, длина АВ – хорды дуги гребня АМВ будет соответствовать 360 мм в соответствии с рисунком 3.3.

При продольном смещении одной из букс более 2 мм происходит перекос колесной пары на угол а и возникает предварительный забег гребня X в соответствии с рисунком 3.2, б. Контакт же точки Мс боковой гранью головки рельса, как исключение, возможен только тогда, когда ось колесной пары

перемещается в горизонтальной плоскости перпендикулярно к продольной оси рамы тележки и рельсовой колеи.

При перекосе КП относительно рельсовой колеи, условная точка Д, рас­положенная на поверхности гребня, будет взаимодействовать с боковой гранью головки рельса. Касательная к точке Д в соответствии с рисунком 3.3 образует угол перекоса а.

При диаметре круга катания колеса 1050 мм и перемещении центра одной буксы на 2 мм в продольном направлении угол набегания а, рад, в соответствии с рисунком 3.2, в, точки Д находят по выражению

Задавая значения продольного перемещения центра буксы лЛТ, в зависимости от состояния шарниров (от 1 до 12 мм), находим значения углов набегания, заносим в таблицу 3.1.

Определив угол набегания колеса на рельс, можно установить величину забега гребня X, мм [55]. Результаты расчетов сведены в таблицу 3.2.

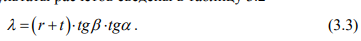
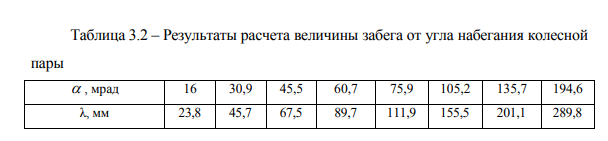
В отношении параметров забега обстоятельство еще более усложняется наличием на тепловозах одностороннего привода, упругих венцов зубчатого колеса, опорной-осевой подвески и зазоров в моторно-осевых подшипниках, особенно при движении по кривым различного радиуса и с различной скоростью. Состояние буксовых поводков и обрезиненных шарниров создает условия постоянного перекоса осей КП. В результате перекоса оси КП гребни бандажей взаимодействуют с боковыми гранями головок рельсов, обеспечивая обоюдный износ поверхностей, при высоком силовом воздействии на путь, с учетом скорости взаимодействия гребня У_вг с рельсом.

Исследования кинематики движения колесных пар

Сложность задачи математического моделирования движения колесных пар объясняется многообразием факторов, которые оказывают влияние на механизм взаимодействия сложного профиля бандажа с рельсом в эксплуатационных условиях. К тому же, на данный момент времени крайне мало работ, посвященных теоретическим исследованиям в этой области.

Первые подходы к изучению сопротивления качению колес по рельсовой колее приведены в изданиях [116-120]. Гипотеза математического моделирования свободного извилистого движения одиночной КП впервые была опубликована в работе Клингеля [121]. Разноплановые гипотезы в области кинематики и динамики взаимодействия колес с рельсами и их обоснование приведены в далеко неполном перечне работ [6, 8, 9, 32, 83-89, 122-126].

Анализ работ показывает, что в их основу положены сомнительные положения или значительно упрощен принцип расчетных схем кинематики движения колес по рельсам, который не может удовлетворять практическую реальность текущего момента. Заслуживают внимания дополнения теории несвободного движения железнодорожных колес в работах Н.П. Петрова, Н.И. Карташева, Н.Е. Жуковского, Б.Н. Веденисова, И. Рокара.

В диссертационной работе для обоснования механизма взаимодействия железнодорожного колеса с рельсом использована математическая теория циклоидальных кривых, в основу которой положены фундаментальные законы движения круга без проскальзывания, получившие математическое обоснование в работах: Е. Торичелли, В. Вивиани, (учеников Г. Галилея), Г. Персонье (Роберваль), Б. Паскаля, Р. Декарта, П. Ферма. Применение математических свойств циклоиды в области практической и прикладной механики обстоятельно изложено в работах: Х. Гюйгенса, И. Ньютона, Г. Лейбница, Иогана Бернулли и Якоба Бернулли, Л. Эйлера, Ж. Лагранжа.

В основу адаптации фундаментальных положений циклоидальных кривых, к процессам движения железнодорожного колеса и механизма его взаимодействия с рельсом, использованы математические свойства циклоиды. Наглядным обобщающим свойством циклоиды является график траектории движения условной точки окружности, спроектированный на вертикальную плоскость в соответствии с рисунком 3.4. Арки образует условная точка А, принадлежащая производящему кругу, когда круг катится по прямой (направляющей прямой) неограниченно долго. Отдельные арки соединяются в точках (остриях), представляя бесконечный ряд арок. Эти точки называются точками возврата циклоиды и соответствуют самым низким положениям условной точки А, перемещающегося круга [90].

Самые высокие положения находятся посредине между точками возврата; эти «наивысшие точки» называют вершинами циклоиды. Отрезок прямой линии между двумя соседними точками возврата, равный 2пг, является основанием одной арки циклоиды.

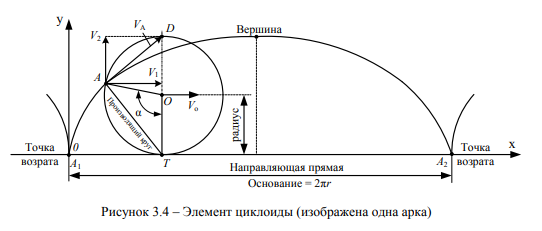
Траектория циклоиды в плоскости движения определяется уравнениями

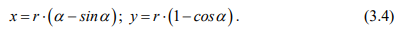
Если из уравнений (3.4) исключить угловой параметр a, то в прямоугольной декартовой системе координат параметрическое уравнение циклоиды принимает вид

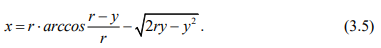
Для математического исследования свойств, параметрических соотношений и зависимостей циклоидальных кривых, необходимо выполнить геометрическое их построение. Для этого выбираем направляющую прямую NX циклоиды в соответствии с рисунком 3.5, где r радиус производящего круга и точку А, принадлежащую кругу.

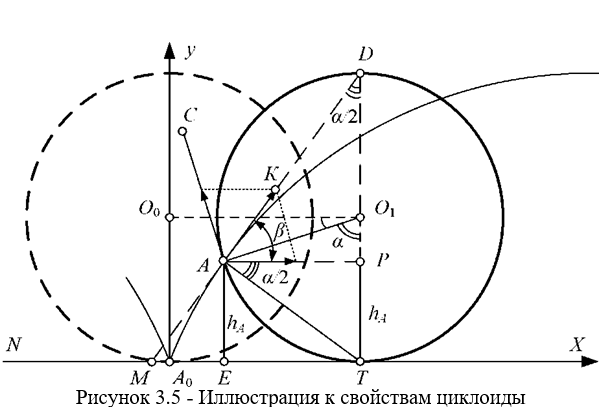
При перемещении центра круга О₀ в положение О, точка А будет перемещаться по дуге А А в соответствии с рисунком 3.5, а центр круга, по прямой ОО, параллельной ЫХ, на расстоянии О А = г от нее. Отрезок АР расположен параллельно направляющей прямой. Прямая АС – перпендикуляр к радиусу ОА. Если от точки а отложить равные отрезки на АР и АС, то получим ромб, а диагональ АК ромба будет касательной МАК к циклоиде в точке А.

Детализация, систематизация, обобщение и адаптация свойств циклоиды

Это построение в соответствии с рисунком 3.5 – чисто геометрическое, хотя получили его, используя понятия механики качения круга. В дальнейшем необходимо использовать математику и обойтись без помощи механики.

Оставляя громоздкие и подробные доказательства свойств циклоиды [90-92], запишем первое из основных в соответствии с рисунком 3.5.

1. Угол между касательной к циклоиде (в произвольной точке) и направляющей прямой / равен дополнению до 90° половины угла а/2 поворота радиуса производящего круга.
2. Угол между нормалью к циклоиде (в любой ее точке) и направляющей прямой равен половине «основного угла» – а/2.
3. Нормаль к циклоиде всегда проходит через «нижнюю» точку Т производящего круга, которая является мгновенным центром поворота круга с направляющей прямой. Следствием этих свойств является: угол между касательной и нормалью – прямой, т.е. как угол, вписанный в окружность производящего круга. Поэтому он должен опираться на диаметр круга ТО. Такие зависимости соотношений геометрических фигур в круге формируют следующие основные свойства циклоиды.
4. Касательная к циклоиде всегда проходит через «верхнюю точку О производящего круга».
5. Синус угла, между касательной к циклоиде в точке А и вертикалью РТ, соответствует корню квадратному из высоты ^ точки А (Н_А = РТ)

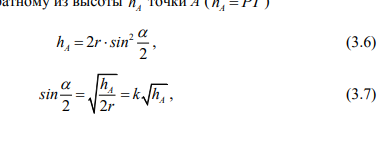
где через к обозначена постоянная для данной циклоиды величина, определяемая диаметром круга

Длина одной арки циклоиды в соответствии с рисунком 3.4 равняется восьми радиусам производящего круга, что на 27,3 % больше

Площадь, ограниченная аркой циклоиды и ее основанием, равна утроенной площади производящего круга

Анализ механизма движения и взаимодействия железнодорожного колеса с рельсом

Характер произвольного расположения условных точек А, Б и В, находящихся на профиле бандажа колеса железнодорожного подвижного состава представлен на рисунке 3.6.

Точка А находится на производящем круге с радиусом г_А, точка Б – на

гребне бандажа (радиус г_Б > ^), точка В – на конической части профиля (радиус ^ГВ < ^ГА ⁾.

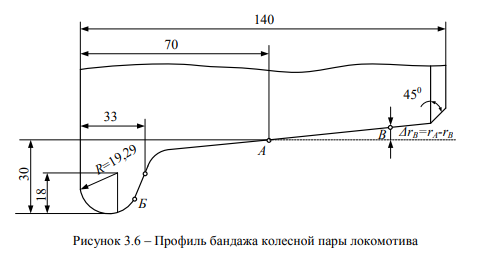
При качении колеса по рельсу на прямом участке пути точка А описывает обыкновенную циклоиду в соответствии с рисунком 3.7, а.

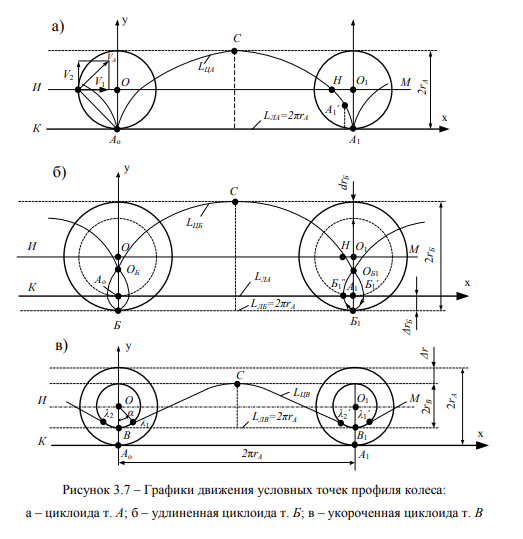
Точка Б расположена на условном топологическом круге сечения бандажа и жестко связана с производящим (образующим) кругом, будет двигаться вместе с колесом и опишет кривую, получившую название «удлиненная циклоида» в соответствии с рисунком 3.7, б. Точка – В находится на круге радиусом меньше образующего г_Б < ^ на Лг_в и при движении описывает кривую, которую называют «укороченной циклоидой» в соответствии с рисунком 3.7, в. Прямая ИМ – проходит через центры О и О1 топологических кругов и называется линией центров циклоид.

Из фундаментальных законов движения голономной системы и ее топологических кругов следует, что все три точки А, Б и В, принадлежащие одному колесу, имеют различный характер траектории в соответствии с рисунком 3.7, но определяются едиными математическими законами конкретных параметрических уравнений (3.4) и (3.5).

Используя уравнения (3.4) и (3.5), находим угловой коэффициент касательной в каждой точке циклоиды, который равен значению производной у’_х в этой точке, т.е.

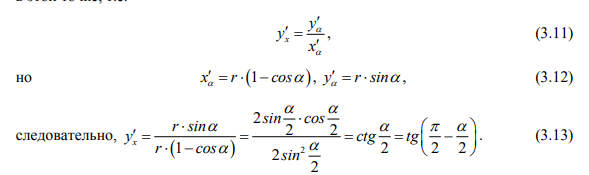
находятся на прямых БО и Б1О1, перпендикулярных направляющей обыкновенной циклоиды, а траектория точки Б соответствует свойствам циклоиды «обыкновенной». Эти точки находятся уравнением

в рассматриваемом случае ( y < y_o) имеет единственный положительный корень;

– точки \ и принадлежат каждой арке укороченной циклоиды в соответствии с рисунком 3.7, в и называются точками перегиба. Соответствующие значения параметра центрального угла а укороченной циклоиды определяются из уравнения

Координаты точки /\ находят по уравнениям

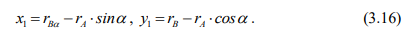
Координаты точки /\ соответственно по уравнениям

Следовательно, траектория условной точки В находится в параметрической зависимости с траекторией точки А до определенных значений. Точке \ соответствует значение координат: x = 0,46 – r^; y = 0,63 – ^. Координаты точки Л₂: x₂ « 5,8-r^; y₂ = 0,63- ^.

Аналитически и экспериментально установлено, что циклоиды, принадлежащие одному колесу с параметрами у_о, \ и , имеют одинаковую кривизну , в частности для обыкновенной циклоиды

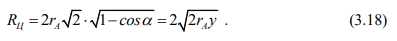
Если радиусы r_B и r_s выразить через их диаметр d, то радиус кривизны для любой циклоиды с математически обоснованным графиком и соотношениями будет определяться как

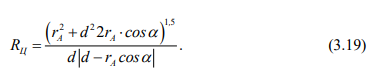
Таким образом, на основе математических законов соотношения параметров циклоид получена возможность с обоснованной корректностью прогнозировать, контролировать и определять кинематические характеристики траекторий точек, находящихся на топологических кругах сечений профиля колеса, имеющего высокую степень голономных геометрических, механических и кинематических связей, при условии жесткого закрепления колес на оси колесной пары.

Метод определения скорости взаимодействия колеса с рельсом

Скорость взаимодействия колеса с рельсом

Движение круга (колеса) по рельсу принято описывать уравнениями плоскопараллельного движения тела как неизменяемой системы в соответствии с формулой Эйлера и теоремой Даламбера [93]: всякое движение свободной неизменяемой системы в бесконечно малый промежуток времени может быть разложено:

• на поступательное движение со скоростью некоторой точки тела;
• вращательное движение вокруг мгновенной оси, проходящей через эту точку.

В свою очередь, эта теорема находится в полном сочетании с теоремой Даламбера.

• «всякое движение твердого тела, имеющего неподвижную точку, в бесконечно малый промежуток времени приводится к вращению вокруг мгновенной оси, проходящей через неподвижную точку».

Таким образом, мгновенным центром поворота точки А является точка контакта колеса с рельсом Т в соответствии с рисунком 3.5. Только при этом условии точка А будет совершать движение по траектории циклоиды в интервале А₀-А₁ в соответствии с рисунком 3.7, а, равном 2пг_А (свойства циклоиды 1, 2 и 3). Так как путь точки А по траектории Ьщ больше расстояния 2пг_А на 27,3%, то, согласно теореме Даламбера, в условных точках возврата («замирания»), в бесконечно малый промежуток времени, можно записать у = 0 [92-94]. Так как круг катится с равномерной скоростью у относительно центра О, а центр перемещается с равномерной скоростью у = у, то точка А совершает сложное движение относительно точки Т. Вектор скорости центра у = 2л /1 расположен параллельно основанию циклоиды. Вектор окружной скорости У₂ направлен по касательной к окружности. Результирующую и искомую скорость у находим по правилу сложения скоростей, и она будет направлена по диагонали ромба под углом 45⁰ к основанию циклоиды и к скорости у (свойства циклоиды 4, 5). Так как cos 45⁰ = л/2 / 2, то

В силу равномерного поступательного перемещения у и вращения у_А, в точках возврата у = у,, что и будет характеризовать скорость взаимодействия контактирующих поверхностей. В этом случае скорость взаимодействия колеса с рельсом будет равна у .

Аналитическое подтверждение результатов определения скорости геометрическим методом основано на свойстве перпендикулярности вектора и нормали у ± ТА (свойство циклоиды 3). Так как прямой угол ТАЭ опирается на диаметр, то вектор у проходит через точку В. Составляя пропорцию у_а/ ТА = у/ ТО и замечая, что ТО = г, а ТА = 2rcosа, находим

Выражения (3.20) и (3.21) свидетельствуют о том, что скорость взаимодействия колеса с рельсом у имеет сочетание с диаметром колеса, а также зависит от расположения условной точки на профиле бандажа.

Кинематические параметры точки Б, расположенной на гребне бандажа

Движение точки Б происходит по более сложной траектории, чем точки А в соответствии с рисунками 3.7, б и 3.8. Если точка Б в соответствии с рисунком
3.7, б достигает уровня горизонтальной плоскости поверхности головки рельса КХ, то в этот же момент центр оси и колеса О будет находиться на расстоянии отрезка дуги круга с радиусом г_А + Дг_Б от условной нормали к направляющей циклоиды в точке возврата. Графики движения точек А и Б дают наглядное подтверждение, что они проходят различные расстояния и 8^ за одно и то же время.

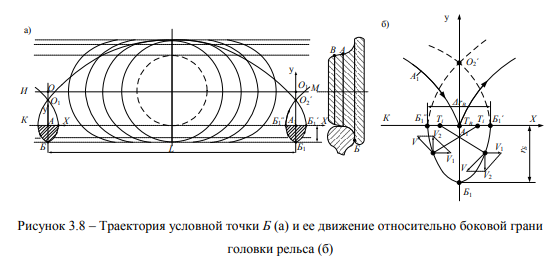
Точка А проходит расстояние, равное длине дуги обыкновенной циклоиды = 8 • ^ в соответствии с рисунком 3.7, а, а точка Б, соответственно, Ь_Б = 8 • г_Б . При движении точки А к положению А\ в соответствии с рисунком 3.8, б точка Б будет находиться в точке Б[ и с этого момента начинает двигаться вниз к Б₁ и в противоположную сторону от поступательного движения центра О и точки А. В момент касания точкой А₁ поверхности рельса точка Б₁, располагается на нормали к центру колеса ОАБ в соответствии с рисунком 3.8. После замирания точка А перемещается по циклоиде вверх и вперед (по ходу движения), а точка Б₁ продолжает движение в противоположную сторону от направления поступательного движения центра оси – по траектории Б₁Б₁” до уровня плоскости КХ. Когда точка Б! достигает уровня КХ (снизу), точка Б”, после этого перемещается вверх в направлении движения центра колеса и экипажа. Заметим, что траектория точки Б на удлиненной циклоиде, также как и точки В на укороченной циклоиде, не имеет точек замирания (точек возврата). На траектории удлиненной циклоиды имеются «петли», по которым движется точка Б от узловых точек О[ до нормали обыкновенной циклоиды.

Аналитическими расчетами и экспериментальными результатами установлено, что графики движения условной точки Б имеют идеальную сходимость, согласно свойствам траекторий удлиненной циклоиды. Движение точки Б при набегании гребня КП на рельсовую колею сопровождается износом металла в соответствии с рисунком 3.9, следы которого остаются на гребне и на внутренней поверхности головки рельса в соответствии с рисунком 3.10 [95, 96].

Параметры проекции графика движения точки Б (петли) зависят от расположения условной точки Б на гребне по расстоянию Д_Б в соответствии с рисунком 3.6 от образующего круга г_А. Проекция на боковую грань головки рельса траектории точки Б, в частности, ниже поверхности головки рельса дает представление исследователям о характере взаимодействия гребня при его набегании на боковую грань головки рельса. Наши объяснения сочетаются с данными работы [95, 96], где приведены результаты

Выводы

1. На основе разработанной комплексной математической модели многозвенной механической системы «тележка – буксовые поводки – буксовые узлы – гребни колесной пары – рельсовая колея» получена возможность определять трехмерное положение оси колесной пары в зависимости от линейных параметров буксовых поводков.

2. Модель многозвенной механической системы дополнена фундаментальными положениями кинематики движения колесной пары, позволяющая оценивать значение скорости взаимодействия гребня с боковой поверхностью головки рельса в зависимости от поступательной скорости локомотива и диаметров его колес.
3. Получена возможность компьютерной визуализации процесса взаимодействия гребней (набегающего, выбегающего) и боковых поверхностей головок рельсовой колеи, в графическом и параметрическом представлении, с учетом перекоса колесной пары.

Список литературы

1. Алексеев, М.В. Воздействие тепловоза ТЭ7 на путь / М.В. Алексеев // Вестн. ВНИИЖТ. – 1957. – №3. – С. 28-30.
2. Мелентьев, Л.П. О влиянии вида подвижного состава на боковой износ рельсов / Л.П. Мелентьев, Т.К. Голутвина // Вестн. ВНИИЖТ. – 1957. – №4. –
3. 46-49.
4. Кудрявцев, Н.Н. Динамика движения колеса с ползуном / Н.Н. Кудрявцев // Вестн. ВНИИЖТ. – 1960. – №2. – С.30-34.
5. Повышение эффективности и надежности работы рельсов / Под ред. А.Ю. Абдурашитова. – М.: Интекст, 2011. – 128 с.
6. Бондаренко, Е.П. Исследование распределения напряжений в головке рельса методом пространственной фотоупругости / Е.П. Бондаренко // Вестн. ВНИИЖТ. – 1957. – №5. – С.47-50.
7. Руссо, А.Э. Исследование распределения напряжений в поперечном сечении бандажа методом фотоупругости / А.Э. Руссо, А.И. Блейхер // Локомотивостроение. – Харьков : Изд-во ХГУ,1970. – Вып. 2. – С. 62-65.
8. Ахметзянов, М.Х. Исследование контактных напряжений в железнодорожных рельсах методом фотоупругих составных моделей / М.Х. Ахметзянов, В.Н. Агуленко // Механика деформируемого тела и расчет транспортных сооружений. – Новосибирск, 1982.- С.61-66.
9. Яковлев В.Ф. Исследование контактных напряжений в элементах колеса и рельса при действии вертикальных и касательных сил / В.Ф. Яковлев // Исследование контактной прочности рельсов: сб. науч. тр. – Л. : ЛИИЖТ, 1962. – Вып.187. – С.3-89.
10. Медель, В.Б. Взаимодействие электровоза и пути / В.Б. Медель. – М. : Транспорт, 1956. – 335 с.
11. Минов, Д.К. Механическая часть электрического подвижного состава / Д.К. Минов. – М-Л : ГЭН, 1959. – 383 с.
12. Королев, К.П. Тележечные экипажи локомотивов для повышенных скоростей движения / К.П. Королев // Труды ВНИИЖТ, 1962. – Вып. 248. – С. 23-30.
13. Алехин С.В. Надежность механической части подвижного состава / С.В. Алехин, Н.С. Продан. – М. : Транспорт, 1969. – 176 с.
14. Апанович, Н.Г. Конструкция, расчет и проектирование тепловозов / Н.Г. Апанович, В.И. Евенко, В.В. Иванов. – М. : Машиностроение, 1969. – 388 с.
15. Домбровский, К.И. Пути снижения износа бандажей колес локомотивов / К.И. Домбровский // Повышение надежности тепловозов : Тр. ЦНИИ МПС,1973. – Вып. 504. – С. 49-61.
16. Николаев, И.И. Динамика локомотивов / И.И. Николаев. – М. : ВИПО МПС,1962. – 319 с.
17. Куценко, С.М. Динамика установившегося движения локомотивов в кривых С.М. Куценко. – Харьков : Высшая школа, 1975. – 132 с.
18. Лазарян, В.А. Силы взаимодействия колес и рельсов, вызванные короткими неровностями / В.А. Лазарян, М.А. Фришман // Вестн. ВНИИЖТ. – 1960. – №6. – С. 9-12.
19. Жуковский, Н.Е. Трение бандажей железнодорожных колес с рельсами / Н.Е. Жуковский // Собр. соч.: В 7 т. – ГТТИ, 1949. – Т. 7. – С.426-478.
20. Андриевский, С.М. Сход колеса с рельса / С.М. Андриевский, В.А. Крылов // Тр. ЦНИИ МПС. – М. : ГТЖИ, 1969. – Вып. 393. – С. 20-41.
21. Коссов, B.C. Снижение нагруженности ходовых частей локомотивов и пути : Дис… д-ра. техн. наук / В.С. Коссов. – М., 2001. – 339 с.
22. Крагельский, В.И. Развитие науки о трении / И.В. Крагельский, В.С. Щедров. – М. : Изд-во АН СССР, 1956. – 234 с.
23. Хрущев, М.М. Абразивное изнашивание / М.М. Хрущев, М.А. Бабичев. – М. : Наука, 1970. – 252 с.