Цикл статей:
Глава 1 – Повышение ресурса колесных пар локомотивов с тележками поводкового типаГлава 2 – Причины и факторы изнашивания бандажей колес локомотивов
Глава 4 – Конструкторское и технологическое совершенствование буксового поводка
Глава 5 – Экспериментальные исследования шарниров буксовых поводков
Глава 6 – Технология и функционально-стоимостный анализ эффективности модернизации буксовых поводков
Конструкторское и технологическое совершенствование буксового поводка
Методы повышения работоспособности буксовых поводков
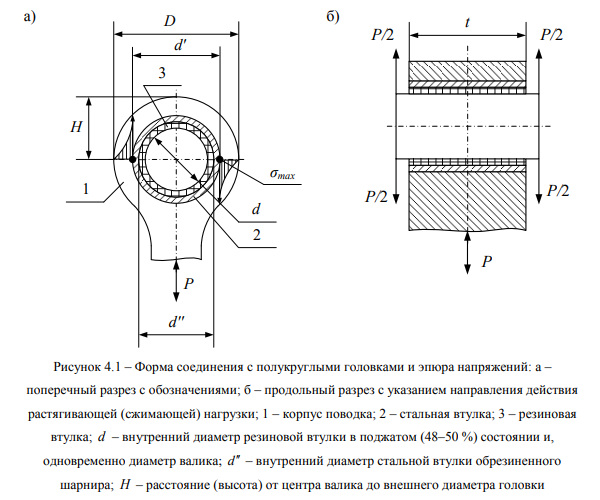
Повышение работоспособности буксовых поводков, обоснование и уточнение их конструкторских и технологических решений, выполнено по методике, изложенной в работе [97]. С точки зрения конструктора, использованы соотношения теоретического коэффициента напряжений К подобных шарнирных соединений в соответствии с рисунком 4.!

где отах – максимальное нормальное напряжение, возникающее в сечении корпуса поводка, Па;
Р – нагрузка, передаваемая от КМБ, через шарниры к раме тележки, Н;
В – внешний параметр головки корпуса поводка, мм;
d 1 – внутренний диаметр отверстия в головке, мм;
£ – ширина корпуса головки поводка, мм.
По данным результатов исследований [97] установлено, что для изделий из стали наиболее приемлемы критериальные зависимости
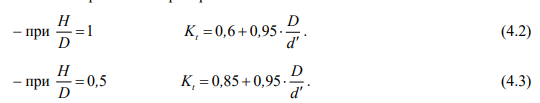
где — – расстояние (высота) от центра головки до ее внешнего диаметра, мм. Следует отметить, что рассматриваемые обрезиненные шарниры буксовых поводков и конструкции, которые были исследованы в опытах [97] имеют отличающие их конструктивные, физические и технологические особенности. Поэтому необходимо использовать наиболее эффективные пути и мероприятия по повышению долговечности обозначенных конструкций и для определения их
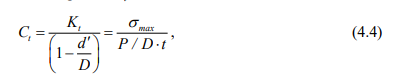
Напомним, что на величину напряжений в примерном конструкторском решении оказывает влияние целый ряд факторов:
- форма головки (полукруглая или прямоугольная);
- соотношения параметров <‘/Б;
- посадка валика с натягом или зазором;
- условия на контактирующих поверхностях валика и отверстия;
- характер нагрузки (статическая, пульсирующая).
В рассматриваемом типовом конструкторском решении имеет место ряд факторов, усугубляющих работоспособность соединения. Во-первых, между валиком и корпусом поводка (ушком) расположены две детали:
- стальная втулка, запрессованная в головку корпуса поводка с неконтролируемым натягом;
- резиновая втулка, с разбросом твердости ±25 %, которая расположена между металлической втулкой и валиком, с примерным поджатием на 48-50 %.
Систематизированные исследования [127] показывают, что прочность проушины быстро падает с увеличением диаметра отверстия. Если отношение диаметра отверстия к ширине (d’ / В) приближается к единице, то такое соединение представляет собой гибкую ленту и по выражению (4.4) наибольшая прочность получается при отношении ^ = 0,43.
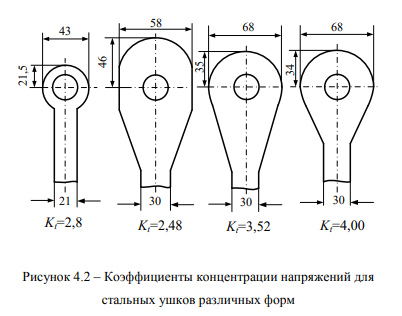
На прочность и долговечность подобных соединений заметное влияние оказывает форма головки. Прямоугольная форма головки уменьшает коэффициент концентрации по сравнению с полукруглой головкой. Влияние формы зависит от относительной высоты головки — / В: для больших значений — / В форма оказывает малое влияние на величину коэффициента концентрации; для средних значений — / В форма оказывает достаточно заметное влияние на коэффициент концентрации; при малых значениях — /В форма головки не установлена. Выборочное сравнение коэффициента концентрации при различных формах головок соединения, по результатам исследований [128], приведены на рисунке 4.2.
Как было отмечено ранее повышение работоспособности и долговечности головки поводка может быть достигнуто за счет полезных напряжений, введением в конструкцию дополнительной втулки с натягом. В работе [129] установлено, что при условии, когда болт (валик) неподвижен, то выносливость ушков увеличивается. В то же время в работе [130] приведено обоснование, что несколько большая выносливость получается при тугой посадке втулки, в сравнении с тугой посадкой болта. А определяющим фактором максимальных касательных напряжений на краях отверстия в поперечном сечении диаметра головки поводка, особенно при отсутствии натяга между втулкой и корпусом поводка, является характер нагрузки.
При нулевой нагрузке со стороны валика натяг сам по себе вызывает определенные касательные напряжения, но при увеличении нагрузки, устанавливается равновесие до определенного возрастания напряжений. Таким образом, весь эффект натяга заключается в увеличении среднего напряжения и уменьшении амплитуды напряжений в критическом сечении. Так как полезный эффект второго больше, то вред первого перекрывается, и выносливость возрастает. Радиальное давление, вызываемое натягом, исключает относительное
движение в критических сечениях поперечного диаметра отверстия, препятствуя возникновению разрушений.
В силу того, что обрезиненные шарнирные соединения буксовых поводков имеют весьма низкую работоспособность и долговечность, то возникла необходимость исследовать и обосновать замену резины на конструкционные материалы, которые должны обладать следующими свойствами:
- соединение «металлическая втулка – конструкционный материал – валик» должно обеспечивать равную прочность элементов при продолжительных периодах его эксплуатации;
- обладать физическими, механическими и технологическими свойствами, которые позволяют снизить коэффициент концентрации напряжения и сохранять эти свойства при знакопеременной эксплуатационной нагрузке.
Выбор и обоснование физическо-механических свойств материала шарниров
С использованием опыта первичных мероприятий в процессе создания долговечных узлов и деталей машин [101, 102] решались задачи:
- изучение комплекса и достоверности условий и причин, определяющих несоответствие типовых изделий;
- обоснование выбора перспективных материалов;
- предварительный расчет конструкционных материалов на прочность и работоспособность;
- целенаправленный мониторинг состояния опытных конструкторских решений в эксплуатационных условиях с анализом их влияния на динамику изменения состояния изделий;
- разработка научно-обоснованных технологических предложений по изготовлению узлов и элементов буксовых поводков;
- принятие и согласование организационных и технологических решений по обучению и сопровождению процесса модернизации буксовых
- поводков с заменой обрезиненных шарниров на конструкционный материал при деповских видах ремонта локомотивов;
- корректировка документации, программы испытаний и сопровождение опытных и контрольных объектов в реальных условиях эксплуатации локомотивов.
Типичное состояние узлов сопряжения рамы тележки с буксами, в соответствии с рисунками 2.1-2.6, обеспечивает нестабильную работу КМБ, повышает уровень динамических составляющих, воздействующих на элементы конструкций экипажной части локомотива и рельсовую колею. Приведенная систематизация неисправностей обрезиненных шарниров буксовых поводков четко ставит на свои места причины и следствия, приводящие к такому состоянию сопряжения, позволяет обратить внимание, прежде всего, на материал и наметить методы и средства повышения долговечности соединений в условиях эксплуатации.
Одним из путей повышения долговечности работы шарниров буксового поводка является использование износостойкого материала в паре трения «металл валика – конструкционный материал шарнира». Преимущество такой пары заключается в способности конструкционного материала в течение продолжительного эксплуатационного периода сохранять стабильные нормативные параметры конструкций. Однако в практике эксплуатации машин известно много примеров, когда положительно зарекомендовавшие себя конструктивные решения, приемлемые для одних условий и режимов работы, оказывались совершенно непригодными для других. Из ряда условий на первый план выходят антифрикционные характеристики материалов.
Выбор материала для применения в шарнирах пары «металл валика – конструкционный материал», выполнен на основе анализа физико-механических свойств, с учетом условий работы и эксплуатационных требований, предъявляемых к узлам экипажной части. В процессе анализа учитывалась стоимость материалов, их доступность, а также опыт применения в машиностроении и локомотивостроении. Рассматривались физико-механические свойства материалов, которые широко используются в машиностроении и локомотивостроении:
- полиамид 6-блочный (обыкновенный и с графитовым наполнением);
- текстолит;
- фторопласт-4:
- бронза.
Основные физико-механические критерии, характеризующие материалы приведены в таблице 4.1. Результаты сопоставления и анализа характеристик материалов свидетельствуют о том, что полиамид с графитовым наполнителем наиболее приемлемый в паре трения «металл – полиамид». Необходимо выделить следующие преимущества полиамида по сравнению с другими материалами:
- исключительно низкий коэффициент трения (антифрикционные свойства улучшены графитом, доля графита 2 %);
- хорошо обрабатывается фрезерованием, точением и сверлением;
- выдерживает высокие ударные нагрузки (от 12 до 15 Дж/см ), что повышает срок службы деталей;
- может работать в узлах трения без смазки по сравнению с бронзой и сталью.
Метод обоснования выбора материала шарнира
Для решения инженерной задачи, в частности повышения долговечности работы шарнирных сопряжений (без резиновых элементов), необходимо: а) исследовать свойства конструкционных материалов, которые обеспечат долговечность подвижного соединения; б) построить расчетный математический аппарат, позволяющий определять их критерии с учетом характера действующих сил и требований, предъявляемых к оборудованию экипажной части.
Для расчета параметров резино-металлических элементов шарнира были использованы общетеоретические положения вариационных принципов теории упругости в цилиндрических координатах. Расчет полого полиамидного цилиндра, составляющего пару трения со стальным валиком, выполнен в постановке задач вязкоупругости в перемещениях и напряжениях.
Перемещения и деформации в цилиндрической системе координат
Положение точки М тела вращения удобно определять цилиндрическими координатами г, в, I в соответствии с рисунком 4.3 [104]. Метод цилиндрических координат связывают обычно с фиксированной осью, на которой выбрано начало отсчета – точка О и направление отсчета осевой координаты. С точкой М и упомянутой цилиндрической координатой связывают тройку ортогональных единичных векторов: единичный вектор г° радиального направления, единичный вектор 6° касательной к координатной окружности в точке Ми единичный вектор , параллельный ()~.
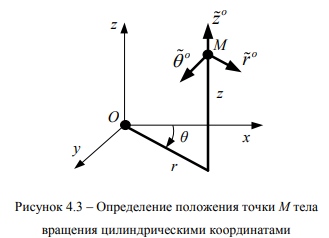
Сплошное тело может занимать два состояния: начальное и деформированное. Положение произвольной точки в начальном состоянии определяется цилиндрическими координатами г, в, I. При переходе тела из начального состояния в деформированное произвольная точка М получает
смещение, которое обозначается вектором и. Этот вектор считается зависящим от координат точки М в начальном состоянии. Вектор смещения и можно представить разложением по единичным векторам г”, в”, I”, связанным с рассматриваемой точкой М

Компоненту иг принято называть радиальным смещением, щ – тангенциальным смещением, а и2 – осевым смещением точки тела.
Если перемещения и градиенты перемещений малы по сравнению с единицей, то формулы для компоненты тензора деформации принимают форму, предложенную Коши [104].
Более наглядно соотношения деформации элемента цилиндрического тела видны при изучении геометрии схемы в соответствии с рисунком 4.4.

Если радиальную деформацию егг в цилиндрической системе координат определять как

где иг – перемещение точки по направлению радиуса – вектора, считая, что точки а и Ь элемента abcd имеют только радиальное перемещение иг, то окружная деформация будет определена как
При малых перемещениях и деформациях совокупность относительных удлинений координатных волокон и сдвигов между ними образует тензор деформаций. Компонентами этого тензора можно характеризовать изменения всех геометрических характеристик окрестности рассматриваемой точки.
Тензор напряжений
Напряженное состояние в точке тела вполне определяется тензором напряжений – шестью напряжениями, связанными с вектором координатной системы.
Каждый из этих векторов можно разложить по координатным направлениям. При этом получим систему уравнений:
Из построения векторов напряжений следует, что а^, авв, а21 представляет собой нормальные напряжения на координатных площадках. Величинами т с различными индексами обозначены касательные напряжения на координатных площадках. При этом первый индекс указывает направление нормали к площадке, а второй – направление, в котором действует это напряжение в соответствии с рисунком 4.5.
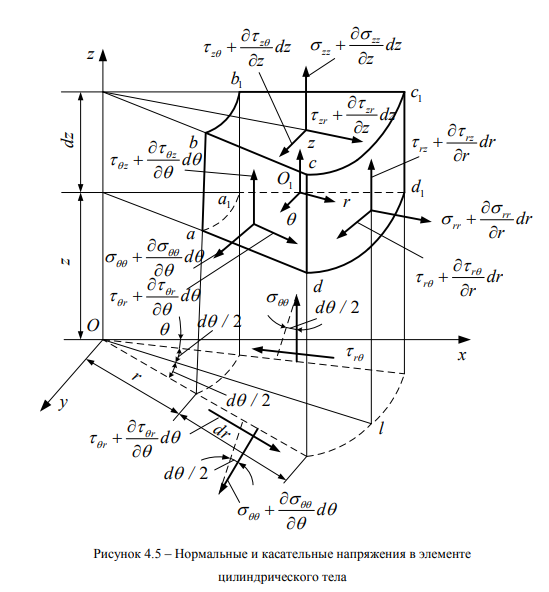
Нормальные напряжения:
- агг – нормальное радиальное напряжение, действующее в радиальном направлении перпендикулярно к граням аЬЬ1а1 и dcc1d1;
- а – нормальное осевое напряжение, действующее в направлении, параллельном оси 02, перпендикулярно к граням ЬЬ1с1с и аа
- аее – нормальное окружное напряжение, действующее в окружном направлении перпендикулярно к граням aЬcd и а^с^.
Касательные напряжения действуют в:
- т2Г – радиальном направлении вдоль граней bb\0\c и aa1dd1;
- – направлении, параллельном оси Oz, вдоль граней abb1a1 и dcc1d1;
- твг – радиальном направлении вдоль граней abcd и a1b1c1d1;
- тгв – окружном направлении вдоль граней abb1a1 и dcc1d1;
- твг – направлении, параллельном оси Oz, вдоль граней abcd и a1b1c1d1;
- т2в – окружном направлении вдоль граней bb1c1c и aa1d1d.
Постановка задачи теории вязкоупругости в напряжениях и деформациях
При замене РТИ в БП на полиамид были решены задачи в напряжениях и деформациях для металлов, а затем – для вязкоупругих. Решение задач линейной теории упругости с определением связей между напряжениями и деформациями выполнено по известным методикам [104].
Материалы, для которых в зависимость между напряжениями и деформациями включается время, называют вязкоупругими. К таким материалам относятся полиамиды.
Для описания процессов деформирования вязкоупругих материалов Больцман разработал наследственную теорию вязкоупругости, в основу которой положен принцип суперпозиций закона Гука. Наиболее общая линейная связь напряжений и деформаций в форме наследственной теории Больцмана – Вольтера, с учетом упруго-постоянных, выражается
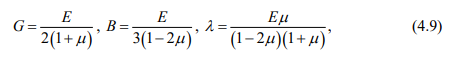
где X, G – коэффициенты Ламе.
Тогда уравнения наследственной краевой задачи в цилиндрической системе координат (x=r• cos(, x2 = r• sin(, x3 = z) на практике аппроксимируют функциями T и K [104]
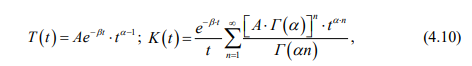

Решение краевых задач вязкоупругости (в напряжениях и деформациях) с учетом статических и динамических воздействий
Статические уравнения вязкоупругости. В настоящее время для решения задач вязкоупругости при статических воздействиях используют ряд методов [104, 105].
Анализ показывает, что для решения предметно-ориентированной конструкции преимущество остается за методом аппроксимации Ильюшина [106]. Метод аппроксимации позволяет решать краевые задачи вязко-упругости в предположении объемной деформации. Для этого необходимо заменить входящие в нее комбинации постоянно-интегральными операторами, которые отражают одновременно протекающие процессы ползучести и релаксации.
В реальной конструкции головка модернизированного поводка состоит из трех элементов: корпус поводка «ушко» (элемент 1), запрессованная в него металлическая втулка (элемент 2), в которую также запрессована полиамидная втулка (элемент 3) в соответствии с рисунком 4.6. Внутренний диаметр полиамидной втулки взаимодействует с металлическим валиком, через который передает на нее и поводок тяговые и тормозные усилия. Элемент 1 изготовлен из стали 35Л; элемент 2 – сталь10; элемент 3 – полиамид. Принимаем параметры длины втулок (по оси 2), согласно конструкции БП, предполагая, что нагрузка и температурное поле элемента 3 остаются неизменными.
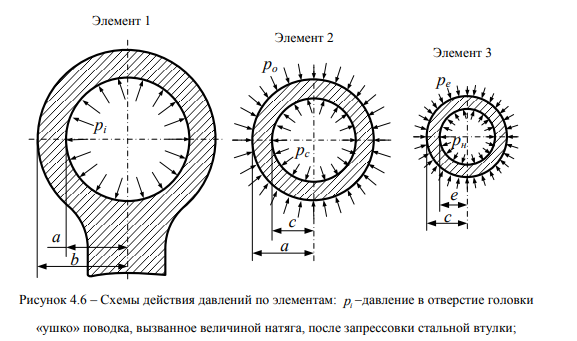
рс -давление в отверстие стальной втулки, вызванное величиной натяга, после запрессовки полиамидной втулки; ре -давление по внешнему диаметру полиамидной втулки, запрессованной в стальную втулку; рн -давление в отверстие полиамидной втулки, вызванное
воздействием металлического валика; а – внутренний диаметр «ушко» корпуса поводка и внешний диаметр стальной втулки; Ь – наружный диаметр цилиндра «ушко» корпуса поводка; с – внутренний диаметр стальной втулки и внешний диаметр полиамидной втулки; е – внутренний диаметр полиамидной втулки
Для определения значений напряжений и перемещений элементов, нагруженных внутренними р и внешними р давлениями, равномерно распределенными по боковым поверхностям, а также при условии отсутствия осевой деформации используем равенства Ламе [107]:
- для элемента 1 решение выполнено методом упругости:
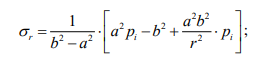

для элемента 2 решение выполнено методом упругости:
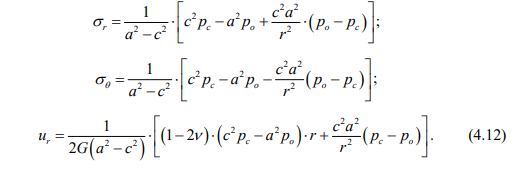

Таким образом, для получения результатов решения поставленных краевых задач нагруженного вязкоупругого цилиндра необходимо знать его внутренний и внешний диаметры, внутреннее р, рс, рн и внешнее ро, ре давления, модули сдвига О и В, функцию ползучести материала П (t).
Динамические уравнения вязкоупругости. Принимая во внимание параметры и составляющие нагрузки, действующие на втулки в процессе движения тепловоза необходимо, учитывать динамическую составляющую. В основу метода расчета полиамидной втулки положены динамические уравнения теории упругости с заменой упругих констант на интегральные операторы Вольтера.
Рассматривались колебания полой полиамидной втулки, внутренняя граница которой медленно меняется под постоянным воздействием на шарнир различных по частоте и амплитуде силовых составляющих, причем
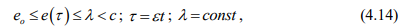
где е0 – начальный внутренний радиус втулки, мм; е(г) – переменный внутренний радиус, мм;


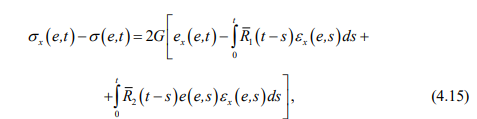

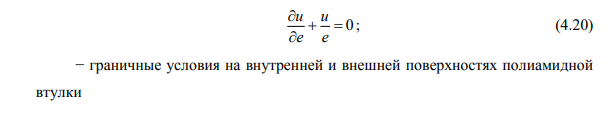



Расчет полиамидной втулки буксового поводка при различных силовых воздействиях на ее внутреннюю поверхность
Расчет напряженно-деформированного состояния (НДС) осесимметричной полиамидной втулки, к которой приложены периодически изменяющиеся во времени нагрузки от металлического валика. При этом металлический валик вращается вокруг своей оси с частотой 3 Гц, что соответствует колебанию рессорного подвешивания тепловоза при движении. Решение задачи выполнено компьютерным моделированием для различных материалов (бронза, текстолит, фторопласт, полиамид с графитовым наполнителем) с целью выявления наиболее пригодного материала, для замены, используемой в данный момент резины. В настоящее время наиболее эффективным и точным средством исследования напряженно-деформированного состояния втулки с учетом характера нагрузок, граничных условий и ряда других факторов, является математическое моделирование методом конечных элементов (МКЭ). Для решения контактной задачи и количественной оценки НДС был использован программный комплекс конечно-элементного моделирования ANSYS 14.5. Workbench [108-110]. Первичными переменными, которые вычисляются в ходе анализа в ANSYS, являются узловые перемещения. В дальнейшем, исходя из вычисленных перемещений в узлах сетки, определяют другие важные параметры: перемещение конструкции; напряжения; деформацию; возникающие реакции в элементах шарнира буксового поводка. Решение нелинейных задач производится пошагово итерационными методами, так как размеры площадок контакта зависят от величины деформации взаимодействующих тел.
В решение контактной задачи с помощью программы численного конечно- элементного метода анализа ANSYS включены следующие основные шаги:
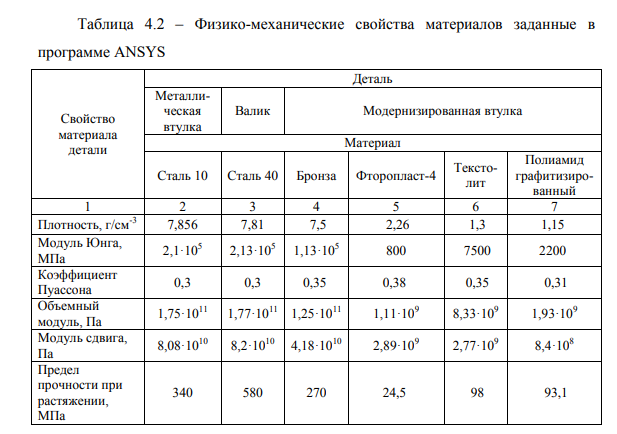
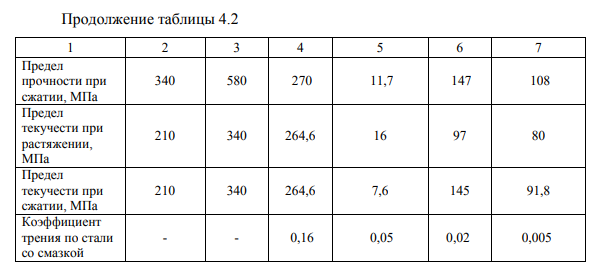
- свойства материалов были заданы при температуре 20 оС;
- приняты физико-механические свойства материалов деталей БП из таблицы 4.2.
- построена конечно-элементная модель в соответствии с рисунком Б.1;
- установлены контактные пары;
- определены целевые и контактные поверхности;
- установлены граничные условия (силы, перемещения);
- заданы опции мотивированных нагрузок для решения задач;
- выполнено решение задач;
- выполнен анализ результатов.
Граничными условиями для моделей являются:
- поверхности наружных диаметров металлических втулок, которые запрессованы в головки поводков (без степеней свободы);
- сила, приложенная к большому и малому валикам, изменялась от 0 до 30000 Н в радиальном направлении;
- учитывалось угловое перемещение поверхности валиков;
- количество шагов решения равнялось 6 (Time [s]);
- температурное поле материалов стационарно и однородно.
Выбор подходящего материала для замены резины выполнен сопоставлением следующих критериев: - износостойкость;
- ударная вязкость (прочность);
- сжимаемость.
Критерий – износостойкость втулки. В процессе движения локомотива обрезиненные шарнирные соединения воспринимают сложные динамические нагрузки, о чем свидетельствует состояние элементов конструкции в соответствии с рисунками 2.1-2.5. К тому же, резиновые втулки имеют высокий коэффициент трения между стальными элементами (валик, втулка). В итоге обрезиненное соединение имеет низкую прочность и износостойкость, а его ресурс не соответствует примерным аналитическим расчетам.
В основу решения задач по определению износостойкости материала положены значения показателей напряжений возникающих на границе между стальным валиком и втулкой.
Вводимыми данными для моделей являлись:
- сила, приложенная к большому и малому валикам, (от 0 до 30 кН) в радиальном направлении;
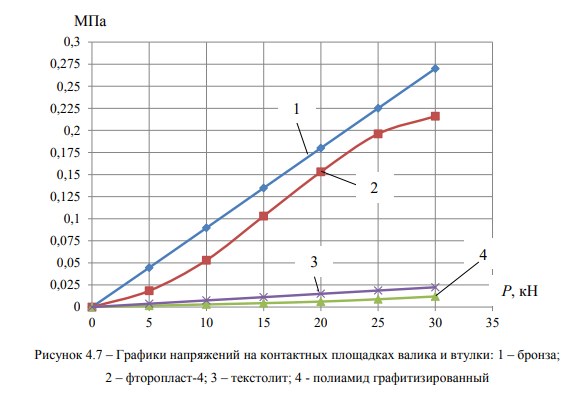
- частота вращения металлических валиков вокруг своей оси – 3 Гц. Результаты расчета напряжений на контактных площадках
модернизированных втулок и валиков буксового поводка от приложенной к валикам силы Р приведены на рисунках 4.7 и Б.2. Результаты расчетов показывают, что графитизированный полиамид обладает низким напряжением и, следовательно, является более износостойким материалов.
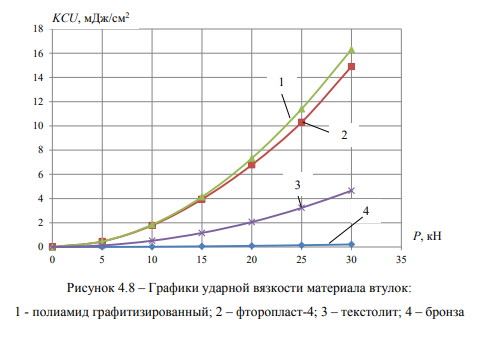
Критерий – ударная вязкость (прочность) втулки. Способность материала модернизированной втулки сопротивляться ударным нагрузкам от валика характеризуется ударной вязкостью KCU и определяется отношением работы, затраченной на разрушение втулки, к площади ее поперечного сечения.
Результаты ударной вязкости KCU модернизированных втулок от приложенной к валикам силы Р приведены на рисунке 4.8. Результаты расчетов показывают, что графитизированный полиамид обладает высокой ударной вязкостью KCU и, следовательно, втулка является более прочной.
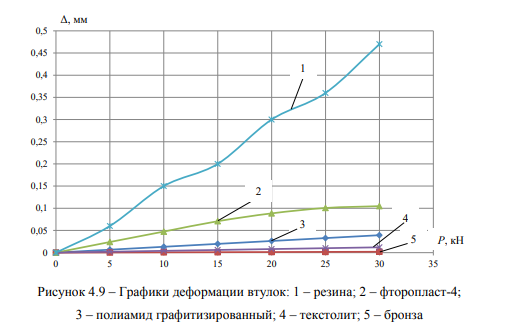
Критерий – сжимаемость втулки. В соответствии с постановкой условий задачи по совершенствованию связей рамы тележки с буксовыми узлами КМБ в качестве одного из критериев принята сжимаемость материала.
Компьютерное моделирование выполнено по пяти материалам. Выбор резины марки «ИРП-1347» обусловлен тем, что она уже применяется в резино- металлических шарнирах (РМШ) буксового поводка. Графики зависимостей общих перемещений внутри материала модернизированных втулок А от приложенной силы Р, представлены на рисунке 4.9. Максимальные перемещения материала у втулки составили: полиамид графитизированный – 0,039 мм; бронза – 0,0019 мм; фторопласт-4 – 0,10 мм; текстолит – 0,011 мм; резина – 0,47 мм. Под действием максимальной тяговой или тормозной нагрузок перемещения возрастают в 1,3-1,6 раз. При этом минимальные перемещения материала увеличивают продольную жесткость втулки, а это приводи к росту сил воздействия локомотива на путь, т.е. решение задачи сводится к нахождению среднего значения перемещений внутри материала втулки. Анализ выполненного имитационного моделирования показал, что наиболее подходящим материалом является полиамид графитизированный.
Результаты расчета общих перемещений внутри полиамидной втулки от приложенной силы приведены на рисунке Б.3.
Выводы
- Наименьшее значение коэффициента концентрации напряжения С, а отсюда и наибольшая прочность головки буксового поводка получаются при отношении внутреннего диаметра отверстия в головке й’ к внешнему параметру головки корпуса поводка В равном 0,43.
- Повышение работоспособности и долговечности головки буксового поводка достигается за счет полезных напряжений, введением в конструкцию дополнительной втулки с натягом.
- Компьютерным моделированием выполнены расчеты напряженно- деформированного состояния шарниров буксового поводка с целью обоснования замены резиновых элементов шарниров на конструкционных материал, который обеспечить сохранение нормативного параметра длины буксового поводка (320±0,2 мм) в условиях эксплуатации между ТР-3 и СР.
- По результатам компьютерного моделирования по критериям износостойкости, ударной вязкости (прочности) и сжимаемости преимущество за графитизированным полиамидом.
Список литературы
- Жаров, И.А. Моделирование изнашивания пары гребень колеса – боковая поверхность рельса в кривых малого радиуса / И.А. Жаров, И.А. Комаровский, С.М. Захаров // Вестн. ВНИИЖТ. – 1998. – №2. – С.15-18.
- Костецкий, Б.И. Трение, смазка и износ в машинах / Б.И. Костецкий. -Киев : Техника, 1970. – 396 с.
- Певзнер, В.О. Влияние ширины колеи / В.О. Певзнер // Железнодорожный транспорт. – 1996. – №12. – С. 36-39.
- Комаров, К.Л. Износ рельсов и колес подвижного состава / К.Л. Комаров, Н.И. Карпущенко. – Новосибирск : СГАПС, 1997. – 153 с.
- Минин, С.И. Причины интенсивного износа колесных пар и рельсов / С.И. Минин // Железнодорожный транспорт. – 1991. – №1. – С. 47-50.
- Плоткин, В.С. О «сверхизносе» колес и рельсов / В.С. Плоткин, В.Д. Кузьмич, Е.Н. Самохин // Железнодорожный транспорт. – 1997. – №8. – С. 51-54.
- Богданов, В.М. Снижение интенсивности износа гребней колес и бокового износа рельсов / В.М. Богданов // Железнодорожный транспорт. – 1992. – №12. – С. 30-34.
- Вериго, М.Ф. Причины роста интенсивности бокового износа рельсов и гребней колес / М.Ф. Вериго. – М. : Транспорт, 1992. – С. 43-44.
- Орлов, М.В. Реализация тангенциальных сил в зоне контакта колеса с рельсом; под ред. М.В. Орлова // Тр. ВНИИЖТ, 1971. – Вып. 664. – С. 21-29.
- Мелентьев, Л.П. О форме контактных поверхностей пары «колесо-рельс» / Л.П. Мелентьев // Вестн. ВНИИЖТ. – 1983. – №5. – С. 47-51.
- Широглазов, В.В. Влияние режимов эксплуатации локомотивов на износ гребней / В.В. Широглазов // Железнодорожный транспорт. – 1992. – №9. – С. 64-66.
- Взаимодействие пути и подвижного состава / Под ред. М.Ф. Вериго. – М. : Транспорт, 1986. – 559 с.
- Ресурс бандажей можно увеличить / Д.А. Курасов, В.Б. Дмитриев, В.В. Севрюгов и др. // Вестник ВНИИЖТ. – 1989. – №7. – С. 38-42.
- Вольперг, А.Г. Влияние конструкции ходовых частей и условий эксплуатации на ресурс бандажей колес локомотивов по прокату / А.Г. Вольперг // Вестн. ВНИИЖТ. – 1990. – №3. – С. 23-26.
- Кузнецов, В.Д. Физика твердого тела. Т. IV / В.Д. Кузнецов. – Томск : 2-е изд. Машгиза, 1947. – 239 с.
- Ларин, Т.В. Износ стали в зависимости от твердости и содержания в ней углерода / Т.В. Ларин // Вестн. ЦНИИ МПС, 1956. – №4. – С. 26-29.
- Алехин, С.В. Исследование износа деталей локомотивов в связи с проблемой увеличения их межремонтных пробегов : Дис. … канд. техн. наук / С.В. Алехин. – Л., 1955. – 464 с.
- Андриевский, С.М. Коэффициент сцепления паровозов при движении по кривым участкам железнодорожного пути : Дис. … канд. техн. наук / С.М. Андриевский. – М., 1950. – 166 с.
- Выбор стали для цельнокатанных колес / Т.В. Ларин, И.В. Наумов, В.П. Девяткин, В.Н. Кривошеев // Техника железных дорог. – 1952. – №1. – С. 6-8.
- Курасов, Д.А. Повышение долговечности бандажей колесных пар подвижного состава / Д.А. Курасов. – М. : Транспорт, 1981. – 159 с.
- Беляев, А.И. Как устранить преждевременный износ бандажей подвижного состава / А.И. Беляев, Ю.В. Емельянов, В.Л. Шишакин // Железнодорожный транспорт. – 1997. – №1. – С. 38-41.
- Мелентьев, Л.П. Влияние дефектов подвижного состава на путь / Л.П. Мелентьев // Путь и путевое хозяйство. – 1999. -№10.- С.23-24.