Цикл статей:
Глава 1 – Природа и причины износа рельсов и колес подвижного состава Глава 2 – Параметры устройства рельсовой колеи и их влияние на процесс взаимодействия в системе «колесо-рельс»
Глава 3 – Износ рельсов, колес подвижного состава
Анализ исследований по установлению норм ширины колеи в кривых
Взаимодействие подвижного состава и пути является основополагающим физическим процессом движения вагонов, локомотивов и поездов на железных дорогах.
Именно этот процесс во многом определяет не только реализуемые значения таких важнейших технико-экономических показателей железнодорожного транспорта как нагрузка на ось и статическая нагрузка вагонов, вес и скорость движения поездов, но и основу основ работы железных дорог – безопасность движения поездов.
Условия взаимодействия в системе «колесо-рельс» оказывают существенное влияние на сроки службы элементов пути и организацию его содержания, а значит, и на эксплуатационные затраты железных дорог.
Одним из наиболее действенных средств управления надежностью работы железнодорожного пути и подвижного состава является управление нормами их устройства и содержания. Безусловно, они должны быть увязаны между собой, обеспечивать безопасность движения и минимизацию расходов на техническое обслуживание.
Ширина колеи в прямых, равная 1524 мм (5 футов), в России была принята в 1842 г. в начале проектирования железной дороги Петербург-Москва.
Рельсовая колея в кривых малых радиусов на железных дорогах всех стран устраивается с дополнительным уширением по сравнению с прямыми участками для обеспечения более благоприятного прохождения подвижного состава. Величина уширения в зависимости от радиуса кривой принимается различной.
Впервые вписывание экипажа в кривые исследовал в 1867 г. Д.М. Лебедев. В 1888 г. A.A. Холодецкий, исследуя вписывание в кривые двухосных, трехосных и многоосных экипажей /40/ доказал, что при радиальной установке задней оси двухосного экипажа отсутствуют поперечные проскальзывания ее колес по рельсам, а сопротивление движению является минимальным. Позже к такому же выводу пришел немецкий ученый X. Хейман /41/ В основу расчетов A.A. Холодецкого было положено условие, что полюс поворота экипажа при движении в кривой располагается на перпендикуляре к продольной оси экипажа. Это было подтверждено немецким ученым Юбелякером /42/ и широко используется при расчетах на вписывание экипажей в кривые в настоящее время.
До 26-го съезда инженеров службы пути в 1898 г. уширения устраивались в кривых на одних дорогах, начиная с радиуса 640 м, на других – с радиуса 2100 м. Максимальное уширение колеи составляло 20 мм. На 26-м съезде была принята эмпирически формула для определения уширения колеи, предложенная A.JI. Васютинским,
Из формулы следовало, что уширение необходимо делать начиная с радиуса 1000 м и менее.
К Ю. Цеглинский в 1903 г. /43/ предложил определять уширение колеи из условия радиальной установки задней оси двухосного вагона по формуле
(L + Ь)2s= < (2.1)
где 8 – суммарный зазор между гребнями колес задней оси и головками рельсов; Ь – длина жесткой базы экипажа; Ь ~ величина предварения касания рельса гребнем бандажа головки.
Приняв двухосный товарный вагон длиной базы 3,9 м (округленно Ь Л- Ь ■= 4 л*), как наиболее распространенный в то время по сети, за расчетный, К.Ю. Цеглинский рекомендовал определять уширение по формуле
8000 AS = — 50
где 80 – нормальный зазор между гребнями бандажей и рельсами в прямой (принимался равным 15 мм).
По этой формуле получается, что уширение следует делать в кривых радиусом 533,4 м и менее /43/.
Формула (2.1) применялась и за границей. На германских железных дорогах уширение колеи при радиальной установке двухосного вагона с длиной жесткой базы 3,3 м определялось по формуле
6000 AS = –80
В США Ассоциация инженеров железнодорожного транспорта (AREA) в 1910 г. рекомендовала определять уширение колеи из условия радиальной установки двухосной тележки четырехосного грузового вагона с длиной жесткой базы 2,2 м по формуле
2800 AS = — -S0
Приказом Народного комиссара путей сообщения (НКПС) в 1935 г. в СССР были введены нормы уширения колеи (таблица 2.1), которые в 1936 г. вошли в Правила технической эксплуатации Железных дорог широкой колеи и действовали до 1957 г.
При этом в ПТЭ 1936 г. специально указано, что “ширина колеи более 1546 и менее 1522 мм ни в каких случаях не допускается».
| Таблица 2.1 – Нормы ширины колеи 1935 г.Радиус кривой, м | Ширина колеи, мм. | Уширение колеи, мм | Допускаемые отклонения, мм |
| более 650 | 1524 | 0 | +6 -2 |
| 650-451 | 1530 | 6 | +6 -2 |
| 450-361 | 1535 | 11 | +6 -2 |
| менее 351 | 1540 | 16 | +6 -2 |
Очевидно, что ширина колеи из таблицы 2.1, удовлетворяющая радиальной установке задней оси двухосного вагона с базой Ь – 3,9 м, в еще большей мере (с избытком) удовлетворяет такой установке для тележек четырехосного вагона. В связи с этим в 50-е гг. возобладало мнение, что практически излишняя ширина колеи (избыток) для массовых экипажей, в основном определяющих экономику вписывания подвижного состава в кривые, вредна, в связи с тем, что сильно изношенные колеса в случае наличия седлообразного (желобчатого) проката будут давить на головку рельса, от которой они значительно удалены гребнями, своей выпуклой частью, резко увеличивая контактные напряжения разрушая металл головки. Кроме того, в зависимости от различных случайных причин жесткая база в излишне широкой колее может встать в перекосное положение, при котором внутреннее колесо задней оси упрется в рельс, увеличивая угол набегания, а следовательно, сопротивление движению экипажа, боковой износ рельсов и гребней колес.
Исследования профессоров П.Г. Козийчука, К.П. Королева /44/, М.А. Фришмана /45/, а также обстоятельные исследования ЦНИИ МПС 1951-1955 гг., выполненные под руководством О.П. Ершкова /46/, опытные данные дорог (Московской, Западно-Сибирской, Южно-Уральской) дали возможность в 1957 г. ввести унифицированные нормы содержания колеи в кривых (таблица 2.2), регламентирующие уширение колеи в кривых только при Я < 350 м.
Отклонения от ширины колеи на прямых и кривых участках пути сохранились по уширению +6 мм, по сужению -2 мм.
| Таблица 2.2 – Нормы ширины колеи 1957 г.Радиус кривой, м | Ширина колеи, мм | Уширение колеи, мм |
| 350 и более | 1524 | 0 |
| 349-300 | 1530 | 6 |
| 299 и менее | 1540 | 16 |
На кривых радиусом от 650 до 300 м, содержащихся по новым нормам, при боковом износе рельсов положительный допуск в ширине колеи (+6 мм) увеличивается на величину фактического износа боковой рабочей грани головки рельсов наружной нити. Однако ширина колеи на таких кривых согласно ПТЭ не должна, превышать при радиусе от 650 до 451 м – 1535 мм; 450 до 351 м – 1540 мм; 350 до 300 м – 1545 мм.
На зарубежных железных дорогах уширение колеи в кривых делается различным в зависимости от конструкции экипажей, величины зазоров в колее и мощности верхнего строения пути. Так, в США при подавляющем количестве тележечных вагонов и достаточно мощном верхнем строении пути Американская ассоциация железнодорожных инженеров рекомендует уширение колеи начинать с радиуса 218 м. Это указание соблюдается рядом дорог. Многие дороги начинают уширение колеи с кривых радиусом 350 м.
В Англии уширение колеи начинается с радиуса 203 м, на немецких дорогах с радиуса 300 м /47-59/, на испанских – 400 м.
В 1963 г. основной допуск в сторону сужения колеи на прямых и кривых был увеличен с 2 до 4 мм.
В соответствии с §24 ПТЭ МПС СССР 1970 г. ширина колеи между внутренними гранями головок рельсов на прямых участках пути и на кривых радиусом 350 м и более должна быть 1520 мм.
Ширина колеи на более крутых кривых установлена в соответствии с таблицей 2.3.
Эти нормы обеспечивают свободное вписывание грузовым и пассажирским вагонам.
| Таблица 2.3 – Нормы ширины колеи 1970 г Радиус кривой, м | Ширина колеи, мм | Уширение колеи, мм |
| 350 и более | 1520 | 0 |
| 349-300 | 1530 | 10 |
| 299 и менее | 1535 | 15 |
2.2 Минимальная, максимальная и оптимальная ширина колеи в кривых из условия квазистатического вписывания экипажей
Между рельсовыми нитями и гребнями колес в обычных условиях всегда имеются зазоры, зависящие как от ширины колеи, так и от ширины колесной пары. Величину суммарного зазора между гребнями колес и рельсами можно определить по формуле /44/.
8 = S-q•l (2.2)
(7=7 + 2/1 + 2/*, (2.3)
- где Б – ширина рельсовой колеи в прямом участке, мм;
- д – ширина колесной пары в расчетном уровне, измеряемая на 10 мм ниже поверхности катания, мм;
- Т – насадка колес, Т = 1440 + 3 мм;
- к – толщина гребня, согласно ПТЭ /60,61/ к – 33 мм, ттк = 25 мм;
- /1 – утолщение гребня выше расчетной плоскости, равное 1 мм для вагонных колес и 0 – для локомотивных.
Так как существуют номинальные, минимальные и максимальные значения Б,Т и /г, то соответственно существуют такие же значения колесной колеи д и зазора 8 (таблица 2.4).
| Таблица 2.4 – Размеры колесных пар Колесные пары | Колесная колея, мм | Зазор в колее, мм | ||||
| <7о | Чтхп | Ятах | ¿0 | ^тт | ^тах | |
| Вагонные(С | 1508 | 1489 | 1511 | 12 | 5 | 37 |
| Локомотивные | 1506 | 1487 | 1509 | 14 | 7 | 39 |
Из таблицы 2.4 видно, что при самом неблагоприятном сочетании размеров рельсовой и колесной колеи между гребнями колес и боковыми гранями рельсов остаются зазоры величиной 5…7 мм.
Минимальная ширина рельсовой колеи определяется возможностью прохождения колесной пары, имеющей наибольшие размеры, *
$тт = Ятах = 1443 + 2 ■ 33 + 2 ■ 1 = 1511 ММ
При меньшей ширине колеи возможно заклинивание колесных пар.
Согласно ПТЭ ширина колеи менее 1512 мм не допускается, поэтому при появлении размеров рельсовой колеи 1512 мм и менее движение поездов прекращается и производится перешивка пути.
Максимальная ширина рельсовой колеи определяется возможностью провала колесной пары, имеющей минимальные размеры. Провал колеса внутрь колеи возможен тогда, когда одно из колес прижато гребнем к боковой грани рельса, а второе катится по выкружке рельса элементом с конечностью 1:7:
$тах = 7тт + ^Чпт + /Л + а — — Т (2.4)
- где а – ширина бандажа колеса; 1г– расстояние от точки перехода
- подуклонки 1:20 к 1:7 до края колеса; г – радиус выкружки рельса.
Подставляя численные значения в формулу из (2.6) получим
^тах =1437 + 25 + 1 + 130 – 30 – 13 = 1550 мм. При большей ширине колеи из-за распирающего воздействия колесной пары при гнилых шпалах и изношенных скреплениях возможен провал одного из колес. Согласно ПТЭ ширина колеи более 1548 мм не допускается.
При определении оптимальной ширины колеи за исходную принимают схему свободного вписывания. На рисунке 2.1 представлена схема такого вписывания для трехосной тележки с учетом разбегов, крайних осей.
Для двухосной тележки принципиальная схема сохраняется такой же (без средней оси). Точкой О обозначен центр вращения тележки. При свободном вписывании он находится на задней оси и внутреннее колесо этой оси своим гребнем касается внутренней нити кривой, не взаимодействуя с ней.
Оптимальная ширина колеи в мм определяется по формуле:
$св= Чшах + Ун ~ (2-5)
- где ятах – максимальная ширина колесной пары;
- – стрела изгиба наружного рельса в мм при хорде АВ,
АВ = 2 (Я + Ь); Величина стрелы определяется по формуле, где Я – расстояние от центра вращения тележки О до геометрической оси первой колесной пары, равное в данном случае длине жесткой базы, мм; Я – радиус кривой, мм;
Ь – расстояние от оси первой колесной пары до точки касания гребня колеса с рельсом, определяемое по формуле, где г – радиус колеса по среднему кругу катания;
т – угол наклона образующей гребня колеса к поверхности катания, равный для вагонных колес 60° и для локомотивных 70°.
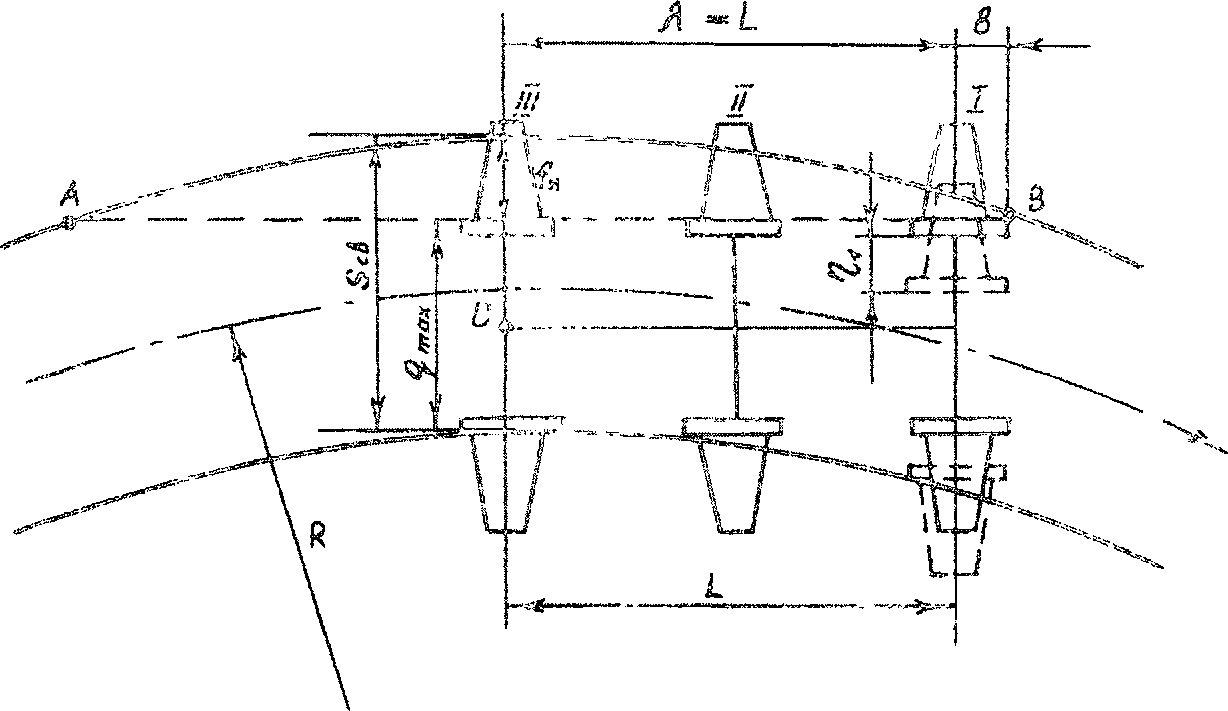
Рисунок 2.1 – Схема свободного вписывания трехосной тележки в кривую
Для электровозов при свободном вписывании Я =L; г — 625 лш; tg70° = 2,747;Ь = (1,72 ■ ¿)/Я.
В этом случае формула (2.6) будет иметь вид
Sce = 1509 + — Л1 (2.8)
Минимальный радиус, при котором будет обеспечено свободное вписывание тележек электровозов, определится по формуле:
При определении минимально допустимой ширины колеи за исходную принимают схему заклиненного вписывания жесткой базы экипажа (см. рисунок 2.2). Учитывая, что заклиненное вписывание допускать нельзя, к полученной по этим схемам ширине Бз прибавляют величину минимального зазора б^тгс между боковой рабочей гранью рельса и гребнем колеса. Для двухосной тележки минимально допустимую ширину колеи мм, определяют из выражения, где и стрелы изгиба наружной и внутренней нитей кривой, отсчитываемые соответственно от хорд, проведенных через точки касания колес с наружной и внутренней нитями. Величины их определяются по формулам:
(X + 2Ь)2 (X – 2Ь)2
Забег колеса определяется по формуле (2.8) при Я = 1/2:
где Ь – длина жесткой базы тележки;
В случае трехосной тележки (рисунок 2.2) ширина колеи определяется по формуле, Здесь X ТЦ — сумма разбега крайних и средней осей.
Полученное значение 5т1П необходимо сравнить с нормативной шириной колеи [8] для принятого радиуса Я кривой.
При самых неблагоприятных условиях Ъ < 0,051 поэтому для двухосных баз можно принять /в = 0. Тогда для обобщенных расчетов за основу примем формулу (2.11). При этом для двухосных экипажей во всех случаях £ Г] = 0.
Для локомотивов Цтах — 1509 мм, 6т1П = 7 мм. В этом случае формула (2.11) будет иметь вид.
Минимальный радиус, при котором будет обеспечено вписывание длинно- базных экипажей в кривые, будет иметь вид.
Результаты расчета вписывания электропоездов в кривые, приведены в таблицах 2.5 и 2.6.
| Таблица 2.5 – Результаты расчета свободного вписывания электровозов в кривые Тип локомотива | Длина жесткой базы ¿о, мм | Поперечные разбеги осей £77 ,мм | Наименьший радиус кривой для обеспечения свободного вписывания локомотивов, м, при нормативной ширине колеи | ||
| 5Н = 1520лш | 5Н = 1525 мм | Би = 1530 лш | |||
| ВЛ10, ВЛ80 | 3000 | ±1,0 | 378 | 268 | 208 |
| ВЛ8 | 3200 | ±2,5 | 382 | 280 | 218 |
| ВЛ23 | 4400 | ±14,0 | 390 | 325 | 277 |
| ВЛ60 | 4600 | ±14,5 | 418 | 349 | 298 |
| ЧС2 | 4600 | ±0 | 964 | 661 | 506 |
| ЧСЗ | 3330 | ±0 | 506 | 348 | 266 |
| ЧС4 | 4600 | ±1,3 | 864 | 613 | 473 |
Из таблицы 2.5 видно, что грузовые электровозы постоянного и переменного тока при ширине колеи 1520 мм свободно вписываются в кривые радиусом 400 м и более. При ширине колеи 1525 и 1530 мм эти электровозы свободно вписываются во все кривые соответственно радиусом более 350 и 300 м, а наиболее массовые электровозы ВЛ10 и ВЛ80 в кривые радиусом более 300 и 200 м соответственно.
Пассажирские электровозы ЧС2 и ЧС4 при ширине колеи 1520 мм имеют затруднительное вписывание в большинстве кривых на перегонах и во все переводные кривые на станциях. При ширине колеи 1530 мм эти электровозы свободно вписываются в кривые радиусом более 500 м.
Таблица 2.6 – Результаты расчета принудительного вписывания электровозов в кривые
| Тип локомотива | Длина жесткой базы Ь0, мм | Поперечные разбеги осей | Наименьший радиус кривой для обеспечения принудительного вписывания локомотивов, м, при ширине колеи | |
| Би = 1520 мм | = 1525 мм | |||
| ВЛ10 | 3000 | ±1,0 | 144 | 89 |
| ВЛ80 | 3000 | ±1,0 | 1—» | 89 |
| ВЛ8 | 3200 | ±2,9 | 164 | 99 |
| ВЛ23 | 4400 | ±14,0 | 138 | 168 |
| ВЛ60 | 4600 | ±16,5 | 132 | 180 |
| ЧС2 | 4600 | ±0 | 334 | 205 |
| ЧСЗ | 3330 | ±0 | 176 | 110 |
| ЧС4 | 4600 | ±2,6 | 267 | 200 |
Анализируя таблицу 2.6, можно сделать вывод о том, что грузовые электровозы при ширине колеи 1520 мм принудительно вписываются в кривые радиусом 160-400 м. В кривых радиусом более 400 м обеспечивается их свободное вписывание. При ширине колеи 1525 мм эти электровозы принудительно вписываются в кривые радиусом 180 м и более.
Пассажирские электровозы ЧС2 при ширине колеи 1520 мм принудительно вписываются в кривые радиусом более 330 м, а при ширине колеи 1525 мм начиная с радиуса, равного 205 м.
Таким образом геометрические расчеты показали, что в кривых радиусом 349-300 м можно устанавливать норму ширины колеи 1525 мм вместо 1530 мм, чтобы иметь большой запас на уширение колеи с учетом допустимой величины бокового износа рельсов.
Однако для решения вопроса о нормах ширины колеи в кривых малого радиуса необходимо провести теоретические и экспериментальные исследования динамического вписывания экипажей в кривые с полученными расчетом нормами ширины колеи, а также эксплуатационные наблюдения.
Динамическое вписывание экипажей в кривую
Общие положения
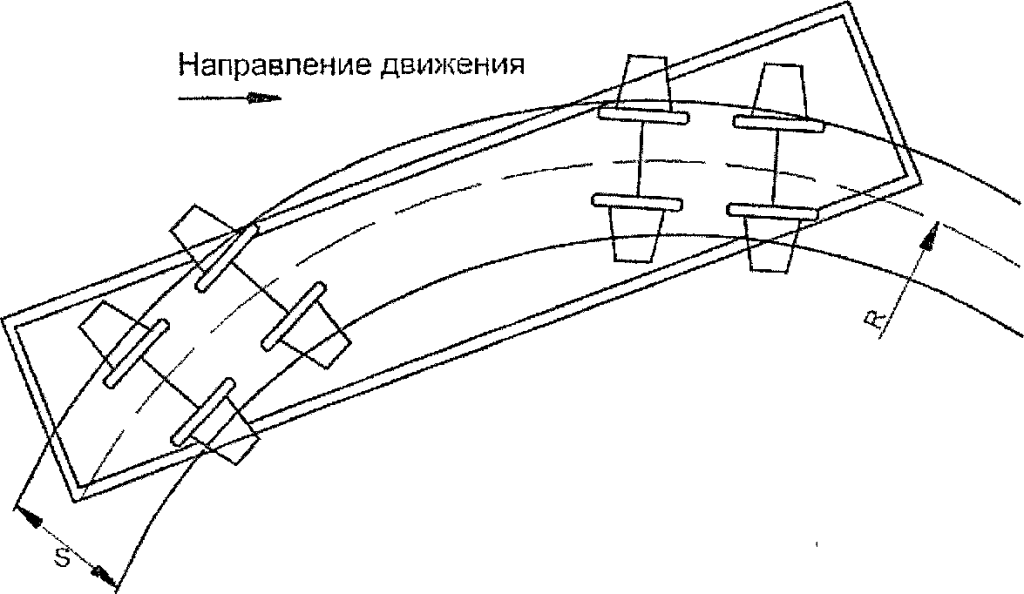
Движение экипажа в кривой складывается из поступательного (вращение вокруг центра кривой) и вращения вокруг точки, расположенной на продольной оси экипажа, называемой центром поворота (рисунок 2.3).
Непрерывное вращение экипажа относительно центра поворота происходит под действием сил, возникающих в точках соприкасания гребней колес направляющих осей с боковой гранью головки рельсов. Это направляющие силы У.
В контактах колес с рельсами возникают силы трения, равные произведению сил, перпендикулярных плоскости касания колес и рельсов, на коэффициент трения скольжения. Эти силы трения создают сопротивление экипажа повороту и поэтому в существенной степени определяют величину направляющей силы.
При непрерывном повороте экипажа в сторону центра кривой возникает центростремительное ускорение.
Центробежная сила как инерционная сила вызывает не только смещение экипажа в сторону наружной рельсовой нити, но и крен кузова на рессорах. Вследствие этого смещается центр тяжести подрессорного и надрессорного строений. Поэтому может возникать перегрузка (или разгрузка) наружной рельсовой нити как от непосредственного действия центробежной силы, создающей опрокидывающий момент, так и за счет веса экипажа, линия действия которого отклоняется от оси колеи /62,63/.
При торможении возникают продольные силы, поперечные составляющие которых также могут изменять направляющие силы.
Для уменьшения центробежной силы и указанных выше неблагоприятных последствий, которые она вызывает, в кривых участках пути устраивают возвышение наружного рельса.

Рисунок 2.3 – Вписывание тележечного экипажа в кривую.
При возвышении наружного рельса центробежная сила уменьшается на величину горизонтальной составляющей веса экипажа.
Расчеты по вписыванию экипажей в кривые позволяют: определить установку экипажа в колее, найти силы, возникающие в точках контакта колес с рельсами и в узлах конструкции экипажа (в сочленении тележек друг с другом, в шкворнях опорных устройств кузова и др.). Это необходимо для установления допускаемых скоростей движения по кривым по условиям прочности, устойчивости пути и безопасности (предотвращения вкатывания гребня колеса на рельс), а также для установления норм устройства и содержания рельсовой колеи. Расчеты по вписыванию проводятся и при проектировании новых типов локомотивов и вагонов для оценки рациональности той или иной конструкции экипажа.
Обычно при расчетах рассматривают стационарное движение экипажа по кривой постоянной кривизны. Для того чтобы учесть силы, возникающие при наличии расстройств в пути или в экипаже, используют экспериментально определенные коэффициенты боковой динамики.
В зависимости от соотношения размеров рельсовой и колесной колеи и сил,
приложенных к жесткой базе экипажа, величины которых определяются в том числе скоростью движения и уровнем непогашенного ускорения, возможны различные схемы вписывания экипажа в кривые /65/.
Свободное вписывание двухосной жесткой базы происходит в случае исправного состояния ходовых частей вагонов, нахождения зазоров и люфтов в пределах допусков, правильно выбранного возвышения наружного рельса в кривой, при котором непогашенное ускорение осн< ±0,3м/с, для грузового движения. Центр (полюс) поворота О жесткой базы в этом случае находится на пересечении продольной оси жесткой базы и радиуса-перепендикуляра, опущенного из центра кривой (рисунок 2.4).
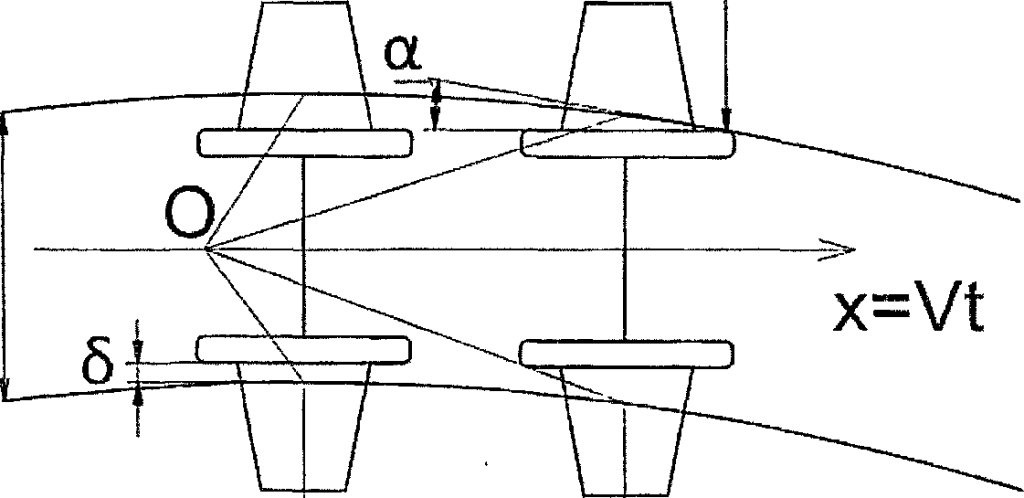
Рисунок 2.4 – Схема свободного вписывания двухосной жесткой базы в кривые
Хордовая свободная установка по наружной нити может происходить при больших скоростях движения и недостаточных возвышениях наружного рельса. Полюс поворота жесткой базы в этом случае находится также на пересечении ее продольной оси с радиусом к ней перпендикулярным за задней осью двухосной базы.
Наружное колесо первой оси тележки набегает на внешний рельс под углом ос. При этом между гребнем внутреннего колеса задней оси и рельсом имеется зазор 5, величина которого зависит от радиуса кривой, размера жесткой базы I и ширины рельсовой колеи 51. Для двухосной тележки грузового вагона при I = 1,85 м зазор 8 может колебаться от 5 до 50 мм.
При полном использовании зазора 5 = 0 будет происходить перекосное вписывание, которому соответствует зазор 84 = 0 и угол набегания ос3. Полюс поворота в этом случае находится между крайними осями экипажа (рисунок 2.5)
Из перечисленного можно определить, что установка экипажа в колее кривой зависит от сил, приложенных к нему, а последние в свою очередь зависят от устройства колеи, радиуса кривой и скорости движения.
Особенности работы пути в кривых требуют повышенных расходов на его текущее содержание, увеличивающихся по мере уменьшения радиуса кривой. Излишнее и недостаточное возвышение наружного рельса в кривых приводят к образованию непогашенного поперечного ускорения осн при достижении значений которого более 10,31 м/с2 увеличиваются поперечные составляющие сил трения на рельсы, которые приводят к возрастанию интенсивности износа рельсов.
Резко возрастает боковое воздействие на рельсы, передающееся, в свою очередь, на промежуточные скрепления.
Определению поперечных сил и моментов, действующих на тележку и рельсовую колею, посвящено много работ. Заслуживают отдельного упоминания разработки доктора технических наук О.П. Ершкова /64,65/ – автора графиков – паспортов вписывания экипажей в кривые.
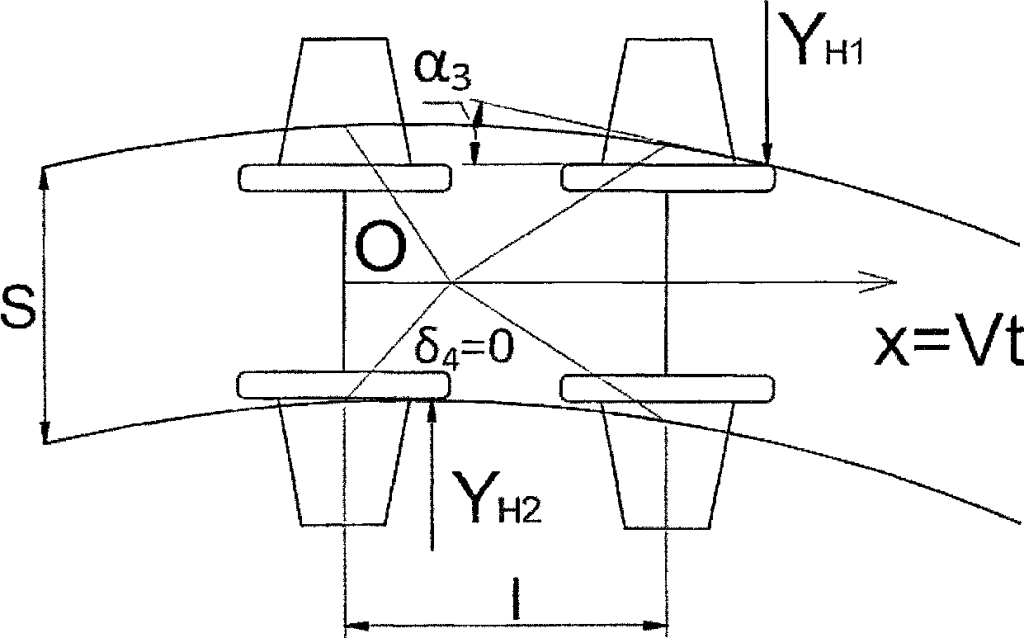
Рисунок 2.5 – Схема перекосного принудительного вписывания двухосной жесткой базы в кривые
Уравнения вписывания экипажей в кривые
Методика составления и решения уравнений вписывания экипажей в кривые и определения поперечных сил излагается в соответствии с работами профессора А .Я. Когана /66,67/.
В этих работах принято, что в горизонтальной плоскости на каждую колесную пару со стороны пути действуют следующие нелинейные силы:
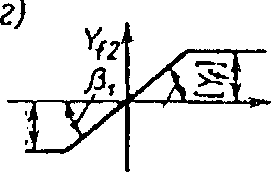
а) поперечная сила трения, нелинейно зависящая от относительного скольжения колеса по рельсу поперек колеи (рис. 2.6 а);
б) момент продольных сил трения, действующих на колесную пару, нелинейно зависящий от углового относительного скольжения колесной пары (рисунок 2.6 б);
в) возвращающая нелинейная сила, появляющаяся при набегании гребня колеса на боковую грань рельса (на рисунок 2.6 в дана зависимость этой силы от смещения с1ц, взятая с обратным знаком).
На рис. 2.6 введены следующие обозначения:
- 11ц – поперечное смещение колесной пары I тележки / относительно сред
- ней линии рельсовой колеи, имеющей отступления в плане (£ = 1 ,п;
- 11ц – относительное поперечное скольжение колесной пары I тележки / (£ = 1^1;/ = 1ГЛ0;
- Уц – относительное угловое скольжение колесной пары Ь тележки / (I = ТТЛО;
сс1,р1,у1 – углы, арктангенсы которых численно равны соответственно жесткости q при набегании гребня колеса на боковую грань рельса, удвоенному коэффициенту крипа зег и величине 2зе2Б^, где 2Б! – расстояние между средними кругами катания колесной пары;
А – зазор в колее между рельсами и гребнями колесной пары; [Уу=-] – ограничение силы трения между колесом и рельсом в поперечном направлении;
[Мг] – ограничение момента сил трения между колесной парой и рельсами.
На рис. 2.7 представлена зависимость направляющих сил, действующих на боковые грани рельса от реборд колес, а также сил трения, действующих на поверхностях катания рельсов в поперечном направлении, от соответствующих аргументов.
На рис. 2.7 введены обозначения:
- ^1(^11/) – направляющая сила, действующая на левую (наружную) рельсовую нить;
- У2(Л1ц) – направляющая сила, действующая на правую (внутреннюю) рельсовую нить;
- ^(Цт) ~ сила трения, действующая на левую (наружную) рельсовую нить в поперечном направлении;
- У^(и1и) – сила трения, действующая на правую (внутреннюю) рельсовую нить в поперечном направлении.
Эксцентриситеты приложения вертикальных сил вц также являются нелинейными функциями случайных аргументов (рисунок 2.8).

Рисунок 2.8 – Зависимости эксцентриситетов приложения вертикальных сил, действующих на наружную (а) и внутреннюю (б) рельсовые нити от смещения колесной пары относительно средней линии рельсовой колеи
Боковые силы, действующие на рельсы, определяются следующими выражениями:
Уы^ц, ии1) = Уг(с11П) + УГ1(и1иУ, УБ2 ит) =
где ит) ~ боковая сила, действующая на наружную рельсовую нить;
Уб2 ^11/) ~ боковая сила, действующая на внутреннюю рельсовую нить. Рамное усилие, передаваемое от пути на колесную пару I тележки /,
Ни{(1П1, и1и) = А(и1и) -/3(сгш).
Функции /1(1%/) и /з(<^1£/) представлены на рисунке 2.6. Наконец, вертикальные силы, действующие на путь при боковых колебаниях экипажа могут быть найдены как линейные функции рамных сил Нц^й^, Щц) и разностей угла боковой качки кузова (р* и углов наклона рельсовой колеи за счет возвышения наружного рельса.
При построении математической модели экипажа кузов, обрессоренные и необрессоренные части тележек считаются абсолютно твердыми телами и деформируемость учитывается только в подвешивании экипажа. Для упрощения расчетной схемы принимается, что параметры одноименных элементов экипажа равны между собой, т. е. все колесные пары и обрессоренные части тележек аналогичны.
В качестве обобщенных координат системы принято:
с^/ – смещение центра масс колесную пару I тележки I относительно средней линии рельсовой колеи, имеющей отступления от прямолинейного положения в плане;
Ут ~ поперечное перемещение центра масс I – ой колесной пары / – ой тележки относительно продольной оси х;
Фт ~ угол между осью £ – ой колесной пары / – ой тележки и нормалью к
продольной оси х;
– поперечное перемещение центра масс / – ой тележки относительно продольной оси х;
гр^ – угол между продольной осью пути х и осью I – ой тележки; у1 – поперечный относ кузова;
тр1 – угол между продольной осью х и осью кузова; <р1 – угол боковой качки кузова.
Дополнительные координаты с1гц удовлетворяют равенствам
Ут ~ ат = У?Ы + аи), (2.16)
где аи – расстояние от центра масс кузова до I – ой колесной пары тележки
Введение дополнительных уравнений (2.16), которые можно рассматривать как вырожденные линейные дифференциальные уравнения, необходимо для того, чтобы разделить нелинейные функции и возмущающие функции (избавиться от инерционных нелинейностей).
Считая, что ось х направлена по касательной к проектной оси пути в сечении центра масс кузова в момент времени 1 = 0, и используя принятые обозначения обобщенных координат (см. также рисунок 2.9), составляются уравнения движения экипажа, движущегося в общем случае по пути с очертанием, допускающим замену горизонтальных поперечных ускорений элементов экипажа, действующих перпендикулярно к оси пути, на вторые производные от их поперечных перемещений (в прямоугольной системе координат) по времени.
Далее определяются обобщенные силы Рь входящие в общие уравнения, описывающие динамику экипажа при колебаниях виляния, относа и боковой качки (боковых колебаниях). На колесную пару действуют поперечные силы трения, пара продольных сил трения, направляющая сила, вызванная набеганием реборды колеса на рельс, и проекции весовых составляющих на ось, проходящую через точки контакта колес с рельсами.
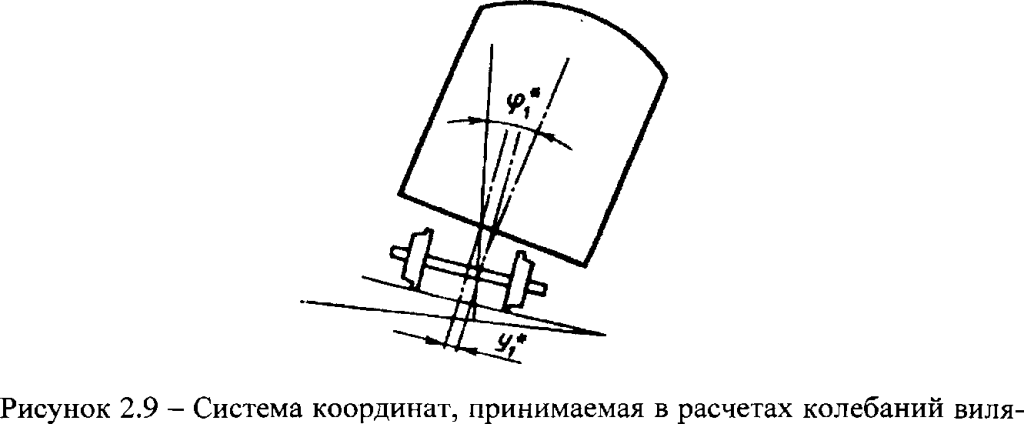
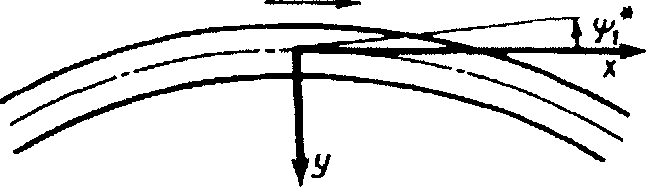
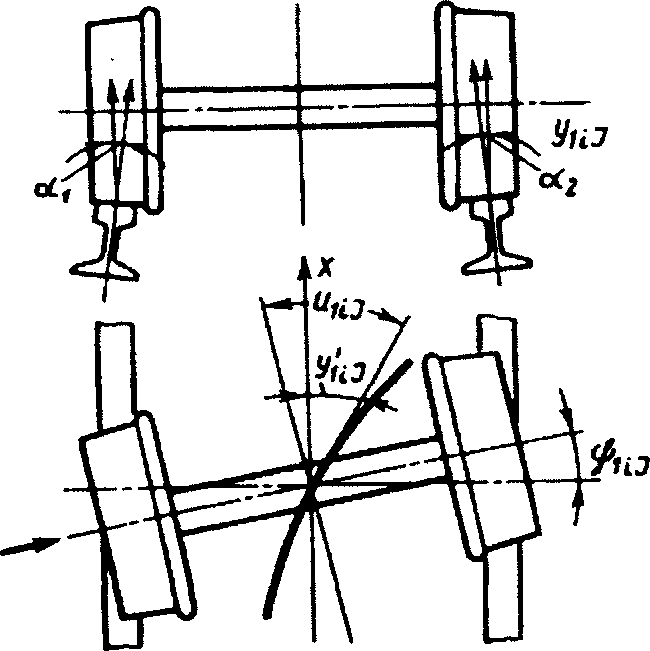
Рисунок 2.10 – Схема движения колесной пары в кривой
Принято считать средним то положение колесной пары в колее, в котором она касается обеих рельсовых нитей равными кругами катания радиуса г (при условии равенства диаметров обеих колес). Положение колесной пары относительно неподвижной системы координат (рисунок 2.10) в момент времени Ь определяется продольной координатой ее центра масс Хц = а}1 + уЬ поперечным смещением центра масс относительно оси абсцисс у1£;, углом поворота хр^ вокруг оси аппликат и углом поворота колесной пары вокруг собственной оси в Колесная пара может отклоняться от линии рельсовой колеи на величину с1гц, связанную с у1и соотношением (2.16).
Пусть 2(}ц – вертикальная нагрузка, передаваемая от колесной пары на рельсы, /1£7 – сила, действующая на колесную пару со стороны пути при отсутствии нагрузки на реборды (перпендикулярно плоскости колеса). Под влиянием силы — /щ происходит местная деформация колес вблизи точек контакта и возникает явление псевдоскольжения, в результате которого точки контакта колес с рельсами перемещаются под углом уги +ФЩ = Щи ^ 0 к плоскости круга катания колеса. Угол Щц принято называть углом увода. Согласно теории крипа при небольших силах Ду имеет место равенство
Щи = Ут + Фт = – (2.17)
где эех – коэффициент крипа в поперечном направлении скольжения. В соотношении (2.17) штрихом обозначена производная по х. Теоретически коэффициент крипа зег зависит от вертикальной нагрузки, однако практически его можно принимать постоянным.
В общем случае поперечная сила трения /1и зависит от угла увода Щц = Уш + Фт нелинейно и ограничена силой сухого трения. Зависимость поперечной силы трения /1£/ = ЛС^!!/) от аргумента Щц представлена на рисунке 2.6 а и может быть записана в виде,
(}ст – статическая вертикальная нагрузка, передаваемая от колеса на рельс;
¡1 – коэффициент трения скольжения.
Рш
Если под влиянием поперечной силы /1£/ колесная пара отклоняется от направления качения, определяемого ее положением в плане (углом 1рш), то под влиянием момента /”21/ изменяется кривизна траектории качения. При отсутствии момента /2ц в связи с конусностью бандажей колесная пара при отклонении от среднего положения в колее на величину (1гц стремится двигаться по траектории с кривизной.
Под действием момента /2ц фактическая кривизна траектории колесной пары определяется величиной.
Согласно теории крипа, при небольших значениях момента /2ц имеет место равенство,
где эе2 – коэффициент крипа при продольном скольжени и Обычно равенство (2.21) записывается в несколько ином виде.
Возвращающая нелинейная сила, появляющаяся при набегании гребня колеса на боковую грань рельса (направляющая сила) зависит от смещения колесной пары относительно среднего положения рельсовой колеи с!-^. График зависимости этой силы от с11115 взятый для удобства последующего изложения с противоположным знаком представлен на рисунке 2.6 в. Аналитически зависимость направляющей силы, взятой с обратным знаком от аргумента (^¡¡может быть представлена в виде.
В формуле (2.24) использованы те же обозначения, что и на рисунке 2.6. Сумма проекций весовых составляющих на ось, проходящую через точки контакта колес с рельсами может быть определена так (см. рисунок 2.10).
При неизношенных колесах б = 0, для изношенных в общем случае из-за наличия проката 5 Ф 0.
Рассмотрим более простую задачу движения экипажа в круговой кривой со средним радиусом (р°) и средним возвышением наружного рельса (к®) . В данном случае функция у^^ + ац)} представляющая собой отклонение средней линии рельсовой колеи от оси х, может быть записана в виде,
где (^ + ац) – случайное отклонение средней линии рельсовой колеи от проектной оси пути в кривой радиуса (р°).
При системе координат, изображенной на рисунке 2.9 уравнение (2.26) справедливо для достаточно малых значений Такого рода ограничение не является существенным, так как силы, действующие на систему, определяются кривизной траектории, постоянная составляющая которой может быть получена при достаточно малых значениях времени I. Можно видеть, что постоянная составляющая второй производной функции у?(х) совпадает со средней кривизной круговой кривой.
Общие уравнения колебаний виляния, относа и боковой качки экипажа (2.25) позволяют вычислить средние значения координат системы аналитически. Для получения уравнений вписывания экипажа в кривую вводятся новые координаты согласно выражениям:
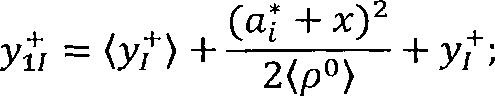
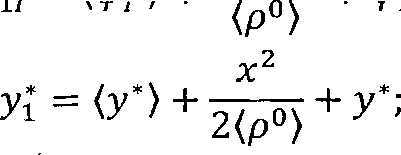
Помимо перехода к новым координатам (2.27) вводится разложение возвышения наружного рельса на постоянную и случайную составляющие, где (кр) – среднее возвышение наружного рельса в кривой; крОт 4- ац) – случайное отклонение возвышения наружного рельса от среднего положения.
Подставляя в систему (2.25) новые координаты (2.27) и разложения возмущающих функций (2.26) и (2.28), полагая возмущения относительно положения изолированного равновесия равными нулю (уц = гри = (1и = у7+ = т/;* = у* = -ф* = ср* = 0, а также, принимая у°(г?С 4- ац) = 4- ац) = 0, получим уравнения вписывания экипажа в кривую со средним радиусом (р°) и средним возвышением наружного рельса (Ьр).
В формулах (2.29) использованы следующие обозначения параметров: 7П* – масса кузова; 2
- – расстояние между рессорными комплектами одной колесной парой
- 2Бг – расстояние между кругами катания колесной пары; т+ – масса тележки;
- Су – жесткость поперечной связи тележки с кузовом; с^ – угловая жесткость поворота тележки относительно кузова; а] – координата по оси х центра масс /- ой тележки; т – масса колесной пары;
- Су – жесткость поперечной связи колесной пары с тележкой; Сф – угловая жесткость поворота колесной пары относительно тележки; ац – координата по оси х центра масс ¿-ой колесной пары /-ой тележки; д – ускорение силы тяжести;
- Я* – расстояние от центра качаний при боковой качке кузова до его центра масс.
Величина Н* в первом приближении может быть определена как расстояние между центрами масс кузова и тележки (по вертикали).
Система трансцендентных уравнений (2.29) определяет положение изолированного равновесия экипажа при боковых колебаниях экипажа в криволинейной
системе координат. В этой системе координат ординаты (Уа), (у/”) и (у*) отсчитываются от проектной оси пути, имеющей постоянную кривизну углы (трц),
(ф7+) и (гр*) отсчитываются от направления касательной к проектной оси пути в точке с соответствующей абсциссой.
Система уравнений вписывания экипажа содержит большую группу линейных уравнений, поэтому для ее решения целесообразно использовать комбинированный метод, основанный на сочетании пробных установок экипажа в кривой и точного решения линейной подсистемы уравнений вписывания (2.29). Процедура решения уравнений вписывания (2.29) сводится к следующим операциям.
Из последнего уравнения системы (2.29) можно сразу найти выражение для среднего значения угла боковой качки кузова (</>*).
Воспользуемся, теперь, равенством (йц) = (уи) содержащимся в системе (2.29) и зададимся начальными значениями координат (уц), представляющими собой поперечные смещения колесных пар относительно проектной оси пути.
Оставшиеся координаты оказываются связанными системой линейных уравнений.
Теперь задача состоит в том, чтобы минимизировать ошибки и добиться необходимой точности решения. Задача минимизации ошибок решения уравнений может быть сведена к исследованию функционала
N п /=1 1=1
который достигает своего минимума и обращается в ноль только тогда, когда ошибки в решении системы уравнений (2.29) отсутствуют.
Нахождение минимума функционала (2.33) может быть осуществлено с использованием алгоритма случайного поиска который применительно к рассматриваемой задаче соответствует методу пробных установок экипажа. Существо этого алгоритма состоит в том, что если сумма квадратов ошибок е2 превышает наперед заданную малую величину £д, установка осей экипажа в колее меняется таким образом, что исходные величины (уц), I = 1,п, I = получают малые случайные приращения, после чего повторяется процедура вычисления функционала (2.33) Если новое значение функционала больше предыдущего, значит попытка была неудачной и процесс поиска продолжается путем добавления других малых случайных приращений к тем же величинам (уи). Если новое значение функционала оказывается меньше предыдущего, но больше величины 8д, то процесс поиска также продолжается, но приращение получают новые исходные величины {уи), т. е. поиск ведется с учетом новой, более удачной установки экипажа в кривой. Процесс поиска минимума функционала е2 прекращается тогда, когда значение его станет меньше заданной величины . Заметим, что задание допустимой величины £о = 1 кН обеспечивает точность решения каждого из уравнений (2.32) \ец\ < 1кН. Решение системы (2.29) дает координаты, определяющие положение экипажа в кривой в специальной криволинейной системе координат. Для большей наглядности и решения габаритных задач удобно перейти к прямоугольной системе координат. Учитывая связь координат экипажа в прямоугольной и криволинейной системах координат (2.27) и полагая х — 0, т. е. рассматривая положение экипажа приостановившемся режиме в момент времени £ = О, получим.
В равенствах (2.34) нижним индексом ноль обозначены координаты экипажа, вписанного в кривую радиусом (р°) с возвышением наружного рельса (Лр), отсчитываемые в прямоугольной системе координат, изображенной на рисунке 2.9.
При решении задачи определения положения экипажа в кривой в установившемся режиме , (вписывание экипажа) важными характеристиками являются абсциссы полюсов поворота тележек, т. е. абсциссы мгновенных центров скоростей движения тележек (при нахождении на них наблюдателя).
Расстояния полюсов поворота тележек от центров их тяжести могут быть определены из выражения.
Расчет вписывания грузового вагона на тележках модели 18-100 в кривые
Для определения величины поперечных сил, возникающих при движении экипажа по кривой, использовалась математическая модель на основе программного комплекса ВЭИП, разработанная под руководством проф. Когана А.Я.
С помощью программы ВЭИП можно получить величину смещения центра масс ¿-ой колесной пары относительно средней линии рельсовой колеи, определить положение полюса поворота жесткой базы тележки и направляющее усилие, появляющееся при набегании гребня колеса на боковую грань рельса.
Результаты расчета вписывания в кривые разных радиусов грузового вагона на тележках модели 18-100 с осевой нагрузкой 210 кН приведены в таблице 2.7 и рисунке 2.11. Из приведенных данных видно, что и направляющая сила уг и полюсное расстояние х1 имеют существенную зависимость от непогашенного ускорения ан и некоторую зависимость от радиуса кривой в диапазоне от 300 до 700 м. При больших значениях радиуса возникает виляющее движение колесных пар и зависимость у1 и х1 от радиуса ослабевает.
Анализ данных также показывает, что на наружную рельсовую нить при свободном вписывании тележек модели 18-100 в кривые передаются только силы трения от поперечного скольжения колес.
На рисунке 2.12 приведены графики зависимости направляющего усилия у1, полюсного расстояния х1 и угла гр^ набегания первой колесной пары тележки на наружный рельс = — при непогашенном ускорении ан = 0.
Наиболее тесную зависимость от радиуса имеет угол набегания гр1. В диапазоне радиусов от 300 до 700 м величина уменьшается в 2,5 раза. При радиусе Я > 900 м значение -ф1 стабилизируется.
| Таблица 2.7 – Результаты расчета вписывания в кривую грузового вагона на Радиус кривой, м | Возвышение наружного рельса, мм | Скорость движения, км/ч | Непогашенная часть поперечного ускорения, м/с2 | Полюс поворота, м | Направляющая сила, кН | Боковая сила, кН | |
| внешняя нить | внутренняя нить | ||||||
| 300 | 150 | 20 | -0,817 | 3,49 | 49,9 | 24,8 | -23,1 |
| 40 | -0,508 | 3,06 | 59,2 | 34,2 | -21,5 | ||
| 60 | 0,006 | 2,65 | 73,7 | 49 | -18,2 | ||
| 80 | 0,726 | 2,31 | 92,6 | 68,3 | -12,9 | ||
| 100 | 1,625 | 2,01 | 114,7 | 90,8 | -4,7 | ||
| 120 | 2,784 | 1,64 | 138,2 | 1 15 | 6,3 | ||
| 400 | 150 | 20 | -0,843 | 3,41 | 51,3 | 26,2 | -22,8 |
| 40 | -0,611 | 3,09 | 58,3 | 33,4 | -21,7 | ||
| 60 | -0,225 | 2,75 | 69,3 | 44,6 | -19,3 | ||
| 80 | 0,315 | 2,45 | 83,9 | 59,4 | -15,5 | ||
| 100 | 1,009 | 2,18 | 101,4 | 77,2 | -10,1 | ||
| 120 | 1,858 | 1,92 | 120,9 | 97,2 | -2,3 | ||
| 500 | 140 | 20 | -0,797 | 3,27 | 54,1 | 29,1 | -22,4 |
| 40 | -0,611 | 3,04 | 59,6 | 34,7 | -21,4 | ||
| 60 | -0,303 | 2,78 | 68,4 | 43,6 | -19,4 | ||
| 80 | 0,129 | 2,52 | 80,2 | 55,6 | -16,4 | ||
| 100 | 0,685 | 2,28 | 94,5 | 70,2 | -12,3 | ||
| 120 | 1,364 | 2,06 | 110,9 | 86,8 | -6,3 | ||
| 600 | 125 | 20 | -0,715 | 3,12 | 57,5 | 32,5 | -21,9 |
| 40 | -0,561 | 2,96 | 62 | 37,1 * | -20,9 | ||
| 60 | -0,303 | 2,75 | 69,3 | 44,6 | -19,4 | ||
| 80 | 0,057 | 2,54 | 79,1 | 54,5 | -16,8 | ||
| 100 | 0,52 | 2,33 | 91,1 | 66,8 | -13,4 | ||
| 120 | 1,085 | 2,13 | 105 | 81 | -8,8 | ||
| 700 | 114 | 20 | -0,655 | 3,04 | 59,8 | 34,9 | -21,3 |
| 40 | -0,523 | 2,91 | 63,6 | 38,8 | -20,6 | ||
| 60 | -0,302 | 2,74 | 69,8 | 45,1 | -19,1 | ||
| 80 | 0,007 | 2,56 | 78,3 | 53,6 | -16,9 | ||
| 100 | 0,403 | 2,37 | 88,7 | 64,3 | -14,1 | ||
| 120 | 0,888 | 2,19 | 100,8 | 76,6 | -10,2 | ||
| 800 | 106 | 20 | -0,611 | 2,98 | 61,5 | 36,6 | -20,9 |
| 40 | -0,496 | 2,87 | 64,9 | 40,1 | -20,3 | ||
| 60 | -0,303 | 2,73 | 70,3 | 45,6 | -19 | ||
| 80 | -0,033 | 2,57 | 77,7 | 53 | -17,1 | ||
| 100 | 0,315 | 2,4 | 86,8 | 62,4 | -14,7 | ||
| 120 | 0,739 | 2,24 | 97,5 | 73,2 | -11,2 | ||
| 900 | 99 | 20 | -0,573 | 2,93 | 62,9 | 38,1 | -20,8 |
| 40 | -0,47 | 2,85 | 65,8 | 41 | -20 | ||
| 60 | -0,298 | 2,72 | 70,6 | 45,9 | -19 | ||
| 80 | -0,058 | 2,58 | 77,2 | 52,5 | -17,2 | ||
| 100 | 0,25 | 2,43 | 85,3 | 60,8 | -14,9 | ||
| 120 | 0,628 | 2,28 | 94,9 | 70,6 | -11,9 | ||
| 1000 | 94 | 20 | -0,545 | 2,9 | 64 | 39,1 | -20,5 |
| 40 | -0,453 | 2,82 | 66,6 | 41,8 | -20 | ||
| 60 | -0,299 | 2,71 | 70,9 | 46,2 | -19 | ||
| 80 | -0,083 | 2,59 | 76,8 | 52,1 | -17,3 | ||
| 100 | 0,195 | 2,45 | 84,2 | 59,6 | -15,3 | ||
| 120 | 0,535 | 2,31 | 92,9 | 68,5 | -12,6 | ||
Рисунок 2.11 – Графики зависимости направляющего усилия и полюса по ворота тележки модели 18-100 от поперечного ускорения
Рисунок 2.12 – Графики зависимости направляющего усилия, полюса пово рота и угла набегания от радиуса при непогашенном ускорении ан = О
Аппроксимация полученных данных в диапазоне —0,5 < ан < 0,5 позволила получить зависимости направляющих усилий уг, боковых сил уБ и полюсного расстояния хг от непогашенного ускорения и радиуса кривой.
Полученные данные достаточно близко совпадают с данными, полученными по методике О.П. Ершкова /64, 65, 68/ и экспериментальными данными /74,75/.
Учет продольных сил при расчете вписывания грузового вагона на тележках модели 18-100
На участках, где осуществляется движение тяжеловесных поездов, особенно с применением рекуперативного торможения, наблюдается повышенный износ рельсов и уширение колеи.
Первые расчеты по вписыванию железнодорожных экипажей в кривые на основе обобщенного метода с учетом возникающих продольных сжимающих сил были выполнены в работе /65/. При расчетах, как показывает практика, можно рассматривать движение поезда как установившийся процесс, а действие продольной силы на экипаж – как квазистатическое.
Для определения средних значений сил в контакте колес вагона, сжатого продольными силами, и рельса необходимо знать средние значения углов поворота осей автосцепок к продольной оси вагона. При оценке горизонтального воздействия на путь вагона, сжатого продольными силами, использовалась методика, изложенная в работе /71/.
Значения дополнительных поперечных сил АН которые передаются на шкворни тележки вагонов от действия продольных сил, определим по формуле
- где N – продольная сила, действующая на вагон;
- Мкр – величина продольной силы, при которой происходит перекос звеньев автосцепки;
- А – смещение сечения пятника кузова относительно оси пути;
- Ьк – база вагона (расстояние между шкворнями);
- – расстояние между упорными плитами автосцепок;
- ш – длина автосцепки;
- 2Ьс – расстояние между осями сцепления автосцепок;
- Ат – величина сжатия, пружин поглощающего аппарата. При И > 100 -г- 150 м можно принимать Ат = 0 без ущерба для точности расчетов;
- И – радиус кривой.
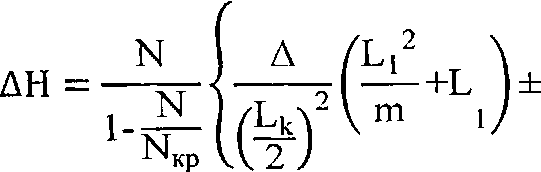
Знак “-” перед последним членом формулы (2.39) означает, что силы приложены к заднему концу вагона, знак “+” – к переднему /72/.
При N < ЫКр формула (2.39) значительно упрощается. В режиме тяги растягивающие продольные силы стремятся сместить кузов вагона внутрь кривой. В режиме торможения сжимающие продольные силы могут быть направлены по- разному в зависимости от схемы расположения вагонов. При направлении поперечных составляющих продольных сил для обеих тележек вагона в одну сторону наружу кривой поперечное воздействие вагона на путь увеличивается; при направлении составляющих в разные стороны (для первой тележки наружу, для второй внутрь кривой) для первой тележки боковое воздействие увеличивается, а для второй уменьшается.
Для грузового вагона на тележках 18-100: Ьк = 8,65 м; 2Ьг = 11,79 м; 2ЬС — 13,92 м; т = 1,0 м; Д= 13 мм; Ат = 0,065, величина Ыкр принята равной 3600 кН.
Определение направляющих и боковых сил по приближенным формулам
Анализ экспериментальных исследований и расчетов на ЭВМ дал возможность использовать для определения поперечных сил вписывания подвижного состава в кривые приближенные формулы /71/ для определения боковых сил, возникающих при расстройствах колеи в плане в кривых и в прямых участках пути:
Значение коэффициента трения /Тр определялось по графику (рисунок 2.13), разработанному лабораторией норм устройства и содержания пути ВНИИЖТ /71/.
При подстановке конкретных значений в формулу (2.41) были получены расчетные формулы для грузового вагона на тележках 18-100
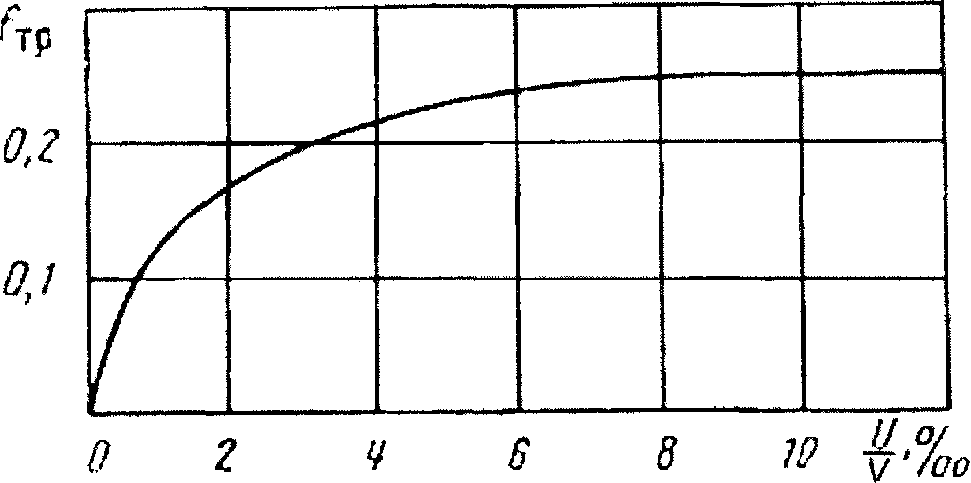
Рисунок 2.13 – Зависимость коэффициента трения скольжения от относительного проскальзывания
Дальнейшее осреднение величин позволило получить обобщенные зависимости направляющих ул и боковых сил УБ для грузового вагона на тележках модели 18-100 от расчетных нагрузок колес Р, непогашенных ускорений ан и продольных сил, возникающих в поезде N
Ух = 0,78РКк + 0,25Ран + К^-, (2.42)
Уб = 0,53 РКк + 0,25 Ран + КМЫ. (2.43)
Величины направляющих и боковых сил, определяемых по зависимостям (2.42) и (2.43) совпадают с результатами исследований, проведенных в /76,77/.
Экспериментальные исследования взаимодействия в системе колесо- рельс в кривых участках пути
Постановка задачи и выбор опытных участков
В СГУПСе на протяжении многих лет ведутся исследования взаимодействия в системе колесо-рельс в кривых участках пути Западно-Сибирской железной дороги.
Целью исследования было выявление влияния параметров рельсовой колеи и ходовых частей подвижного состава на характер этого взаимодействия и интенсивность износа колес и рельсов.
Экспериментальные исследования велись на участке Алтайская — Кузбасс, являющимся частью Среднесибирской магистрали со сложным планом и профилем, высокой грузонапряженностью и осевыми нагрузками; участке Новосибирск — Болотное, являющимся частью Транссибирской магистрали, и участке Инская – Сокур (рисунок 2.14). Характеристики участков приведены в таблице 2.8.
| Таблица 2.8 – Характеристика опытных участков Опытный участок | Конструкция пути | Номер опытной кривой | Характеристика кривой, средние значения | ||||
| радиус, м | возвышение, мм | ширина колеи, мм | бок. износ нар. Р-, мм | пропущ. тоннаж, млн. т | |||
| Алтайская — Кузбасс | Бесстыковой путь с рельсами Р65, промежуточным скреплением КБ, железобетонными шпалами и щебеночным балластом | 1 | 417 | 75 | 1526 | 2,2 | 16,7 |
| 2 | 431 | 72 | 1526 | 2,3 | 16,7 | ||
| 3 | 284 | 86 | 1530 | 9,3 | 53,9 | ||
| 4 | 291 | 88 | 1530 | 7,6 | 53,9 | ||
Продолжение таблицы 2.8
| Характеристика кривой, средние значения | |||||||
| Опытный участок | Конструкция пути | Номер опытной кривой | радиус, м | возвышение, мм | ширина колеи, мм | бок. износ нар.Р-, мм | пропущ. тоннаж, млн. т |
| Звеньевой путь с | 5 | 407 | 110 | 1538 | 12,2 | 467,0 | |
| рельсами Р65, | 6 | 400 | 77 | 1537 | 11,5 | 542,7 | |
| промежуточным | 7 | 392 | 84 | 1535 | 7,7 | 467,0 | |
| Инская – | скреплением ДО, | ||||||
| Сокур | деревянными шпалами и щебеночным балластом | 8 | 370 | 76 | 1532 | 12,2 | 542,7 |
| Бесстыковой путь | |||||||
| с рельсами Р65, | |||||||
| Новосибирск – Болотное | промежуточным скреплением КБ, железобетонными шпалами и щебеночным балластом | 9 | 652 | 81 | 1531 | 9,8 | 473,3 |
Примечание – в таблице указан пропущенный тоннаж с момента проведения последнего капитального ремонта по состоянию на 01.01.2007 г.
Методика проведения эксперимента
В рассматриваемых кривых были проведены комплексные исследования параметров рельсовой колеи и характеристик вписывания подвижного состава с использованием цифровой фото- и видеоаппаратуры. Предварительно определялись следующие параметры: возвышение наружного рельса, ширина колеи, износ рельсов, радиус кривой. Профиль изношенных головок рельсов контролировался с помощью специального шаблона. Кроме того, в кривых к головкам наружного и внутреннего рельсов снаружи колеи устанавливались индикаторы часового типа для определения динамического отжатия рельсовых нитей при проходе поезда. Внутри колеи к головкам рельсовых нитей устанавливались цифровые видеокамеры, которые записывали положение колес относительно рельсовых нитей при вписывании в кривые и передавали видеопоток в режиме реального времени на портативный компьютер. Схемы установки аппаратуры представлены на рисунке 2.15. В
ходе исследований также определялась реальная скорость движения поезда в кривой. (Эти исследования выполнялись под руководством к.т.н., доц. И.А. Котовой) /78, 79/.

Рисунок 2.14 – Вид опытного участка в кривой радиусом 368 м.
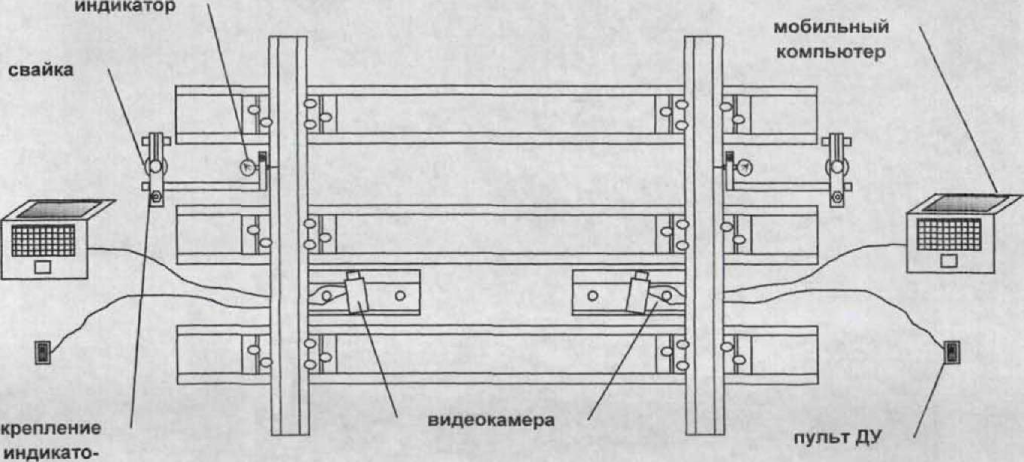
Рисунок 2.15- Схема установки приборов на пути

Рисунок 2.16 – Установка индикаторов часового типа в ходе проведения экспериментов
Контроль за обеспечением безопасности движения поездов и безопасности работников, занятых в эксперименте возлагался на работников дистанции пути. Работы выполнялись в соответствии с «Инструкцией по обеспечению безопасности движения поездов при производстве путевых работ».
Обработка и анализ полученных результатов
В результате покадровой расшифровки были обнаружены некоторые особенности взаимодействия ходовых частей подвижного состава и рельсовой колеи в кривых при различных возвышениях наружного рельса.
Приведенные ниже кадры фото- и видеосъемки показывают, что боковой износ на внутренних нитях отсутствует. На большинстве рабочих граней внутренних нитей кривых отсутствуют даже следы касания гребней колес (рисунок 2.17) /78/, кроме того, стоп-кадры видеосъемки показали наличие значительных зазоров между гребнями колес и боковыми гранями внутренних рельсов при движении и даже при остановке поезда в кривой (рисунок 2.18) /79/. Поэтому утверждения о недостатке ширины колеи в кривых не имеют под собой никаких оснований.
Анализ результатов экспериментов показал, что величины отжатия головок рельсов зависят от конструкции пути, его состояния под влиянием наработанного после капитального ремонта тоннажа и величины непогашенного центробежного ускорения (таблица 2.8). Самые большие по величине отжатия зафиксированы на участке Инская – Сокур, пропустившем 600 млн. т. брутто тоннажа и имеющем изношенные деревянные шпалы с разработанными костыльными отверстиями. Обращает на себя внимание так же то, что отжатие головок внутренних рельсов, как правило, больше, чем наружных.
Рисунок 2.17 – Внутренний рельс кривой радиусом 354 м

В результате расшифровки видеозаписей установлено, что первые колеса вагонных тележек в кривых радиусом 650 м и менее всегда касаются рабочими гранями гребней боковых граней наружных рельсов (рисунок 2.19). Вторые колеса тележек имеют зазоры между гребнями и наружными рельсами. Относительно внутренней рельсовой нити на всех видеозаписях отсутствуют касания гребней колес, как первой, так и второй колесных пар тележек, боковых граней рельсов. Величина зазора между рабочими гранями гребней и рельсов для первой колесной пары тележки определяется шириной колесной пары в рабочем уровне и шириной ко-

Рисунок 2.18 – Зазор между гребнем колеса и боковой гранью внутреннего рельса в кривой радиусом 368 м
В ходе исследования был также выявлен факт динамического отжатия (раскантовки) на 3 – 4 мм рельсов внутренней нити, что в некоторых случаях более чем вдвое превышает динамическое отжатие рельсов наружной нити (таблица 2.9). При чем это явление наблюдалось и на бесстыковом пути, хотя абсолютные значения отжатий здесь были существенно меньше для внутренней нити 2-3 мм, для наружной 1,2-1,6 мм.
Объясняется это тем, что на внутренний рельс передаются большие силы трения по поверхности катания. На наружный рельс кроме силы, направленной наружу кривой, внецентренно через гребень колеса передается в виде сил трения по боковой грани рельса часть вертикальной нагрузки, наклоняющей наружный рельс внутрь кривой, (Это подтверждено расчетом).
Ширина вагонной колесной пары в соответствии с существующими нормами может изменяться от 1511 до 1489 мм. Ширина колеи в месте установки приборов на кривой радиусом 407 м – 1539 мм. В этом случае зазор мог изменяться в зависимости от размеров колесной пары в пределах от 28 до 50 мм /79/. Фактически (рисунок 2.20) /80/ он находился в пределах 38…50 мм. Зазор между рабочими гранями гребней и рельсов второй колесной пары тележки относительно наружной нити находился в пределах 0…35 мм.
Таблица 2.9 – Результаты экспериментов по взаимодействию колес и рельсов в кривых участках пути
| Номер опытной кривой | Информация о поезде | Отжатие головки рельса, мм | ||||||||
| Опытный участок | серия локомотива | скорость движения, км/ч | непогашенное ускорение, м/с2 | наружного | внутреннего | |||||
| ср. | макс. | ср. | макс. | ■ср. | макс. | ср. | макс. | |||
| 1 | ВЛ80 | 48 | 58 | -0,07 | 0,13 | 1,3 | 1,6 | 1,9 | 3,0 | |
| Алтайская – | 2 | ВЛ80 | 49 | 57 | -0,07 | 0,08 | 1,2 | 1,4 | 1,6 | 1.7 |
| Кузбасс | 3 | ВЛ80 | 56 | 61 | 0,32 | 0.48 | 4,6 | 5,6 | 3,5 | 4,8 |
| 4 | ВЛ80 | 47 | 55 | 0,04 | 0,26 | 1,3 | 1,7 | 3,8 | 5,0 | |
Продолжение таблицы 2.9
| Опытный участок | Номер опытной кривой | Информация о поезде | Отжатие головки рельса, мм | |||||||
| серия локомотива | скорость движения, км/ч | непогашенное ускорение, м/с2 | наружного | внутреннего | ||||||
| ср. | макс. | ср. | макс. | ср. | макс. | ср. | макс. | |||
| Инская – Со кур | 5 | ВЛ10 | 50 | 70 | -0,16 | 0,28 | 3,6 | 4,6 | 7,4 | 8,9 |
| 6 | ВЛ10 | 57 | 70 | 0,17 | 0,45 | 2,0 | 2,8 | 7,0 | 9,0 | |
| 7 | ВЛ10 | 46 | 50 | -0,10 | 0,00 | 2,1 | 2,9 | 8,0 | 8,7 | |
| 8 | ВЛ10 | 61 | 70 | 0,32 | 0,56 | зд | 4,0 | 4,2 | 5,4 | |
| Новосибирск – Болотное | 9 | ВЛ10 | 50 | 61 | -0,10 | 0,00 | 0,0 | 0,5 | 2,5 | 3,2 |
Относительно внутренней рельсовой нити зазор фиксировался в пределах
5…45 мм (рисунок 2.17). Таким образом, при движении по кривой радиусом 407 м со скоростями 40 — 70 км/ч реализуется свободное вписывание двухосной вагонной тележки. Касание гребней колес рабочей грани внутреннего рельса не зафиксировано.
Обработка результатов видеонаблюдений, полученных в опытной кривой 6, дала похожие результаты, хотя возвышение наружного рельса в этой кривой было на 33 мм меньше, чем в опытной кривой 5, при одинаковых радиусе и скоростях движения (приложение А).
Данные, полученные в опытной кривой 9, имеющей радиус 625 м, оказались несколько другими. Здесь наблюдается виляние вагонной тележки при движении по кривой с образованием в некоторых случаях зазора величиной 2-10 мм между гребнем первого колеса тележки и боковой гранью наружного рельса.
Похожие результаты получены проф. М.А. Фришманом при исследовании взаимодействия в системе “колесо-рельс” с использованием скоростной видеосъемки /81/.

Рисунок 2.20 – Величина зазора между рабочими гранями внутреннего рельса и гребнем колеса первой оси вагонной тележки (1 путь, 10 мм).
Номер осей
Рисунок 2.21 – Величина зазора между рабочими гранями внутреннего рельса и гребнем колеса второй оси вагонной тележки (1 путь, Ь=110 мм)
| Таблица 2.10 – Величины зазоров между рабочими гранями гребней и рельсов в расчетном уровне, мм Опытный участок | Номер опытной кривой | Наружная нить | Внутренняя нить | ||||||||||
| первое колесо | второе колесо | первое колесо | второе колесо | ||||||||||
| ср. | макс. | мин. | ср. | макс. | мин. | ср. | макс. | мин. | ср. | макс. | мин. | ||
| Инская — Сокур | 5 | 0 | 0 | 0 | 17 | 35 | 0 | 44 | 50 | 38 | 22 | 45 | 5 |
| 6 | 0 | 0 | 0 | 19 | 35 | 0 | 44 | 47 | 35 | 25 | 45 | 5 | |
| Новосибирск – Болотное | 9 | 3 | 10 | 0 | 12 | 25 | 0 | 35 | 39 | 20 | 28 | 39 | 19 |
Больше также величины зазоров между гребнями вторых колес и боковыми гранями внутренних рельсов. Это обеспечивает меньший угол набегания колес на наружный рельс, а, следовательно, и интенсивность износа рельсов в таких кривых.
Приработка поперечных профилей вагонных и локомотивных колес и рельсов происходит довольно быстро независимо от первоначальной формы обточки колес /82/. При этом иногда возникает ситуация, когда набегающее на наружный рельс колесо локомотива, имеющего высоту гребня 30 мм,’ начинает катиться по полке, образовавшейся на боковой грани рельса, а поверхность катания колеса отрывается от поверхности катания рельса (рисунок 2.22 а) /78/.
И.А. Котовой зафиксирован также отрыв поверхности катания вагонных колес от рельсов (рисунок 2.22 б) на опытной кривой 3, имевшей недостаточное возвышение наружного рельса – 88 мм при радиусе 284 м и реализации непогашенного поперечного ускорения 0,48 м/с”. Кроме высокого непогашенного ускорения здесь имел место высокий коэффициент трения между гребнями колес и боковыми гранями рельсов из-за отсутствия смазки.
Качение переднего колеса гребнем по наклонной выработке в головке рельса вызывает сильный перекос вагонной тележки с образованием больших зазоров между гребнем заднего колеса и боковой гранью наружного рельса.
Средние значения углов набегания передних колес тележки модели 18-100 на боковую грань наружного рельса в кривых радиусом 400 м при скорости движения 70 км/ч составили 0,5-0,6°, а максимальные – 1,1° при скорости движения 50 км/ч.

Рисунок 2.22 – Отрыв поверхности катания колеса от поверхности катания наружного рельса в опытной кривой
В кривых радиусом 650 м при аналогичных условиях испытаний среднее и максимальные значения углов набегания составили соответственно 0,35° и 0,8°.
Выводы
- Ширина колеи в кривых с момента возникновения железных дорог рассчитывается исходя из вписывания обращающихся по сети дорог экипажей.
Переход с длиннобазных экипажей паровозов и двухосных вагонов, на короткобазные тележечные экипажи позволил в 1959 г. перейти на унифицированную колею, при которой уширение начиналось с кривых радиусом 350 м и менее вместо 650 м.
Последняя корректировка ширины колеи в прямых и кривых участках произведена в 1970 г., когда со стандарта колеи в 1524 мм перешли на стандарт в 1520 мм. Обосновано это было снижением амплитуды виляния тележек в прямых и пологих кривых, а также уменьшением типоразмеров железобетонных шпал при укладке бесстыкового пути в кривых.
- Анализ результатов квазистатического вписывания в кривые обращающихся по Российским железным дорогам экипажей показал, что наиболее массовые экипажи – пассажирские и грузовые вагоны свободно вписываются практически во все кривые как на перегонах, так и на станциях.
Грузовые электровозы постоянного и переменного тока при ширине колеи 1520 мм свободно вписываются в кривые радиусом 400 м и более. При ширине колеи 1525 мм и 1530 мм электровозы ВЛ10 и ВЛ80 свободно вписываются во все кривые радиусом более 300 и 200 м соответственно.
Пассажирские электровозы ЧС2 и ЧС4 при ширине колеи 1520 мм имеют затрудненное вписывание в большинстве кривых на перегонах и во все переводные кривые на станциях. При ширине колеи 1530 мм эти электровозы свободно вписываются в кривые радиусом более 500 м. вписывание этих электровозов при ширине колеи 1525 мм обеспечивается в кривых радиусом 205 м и более.
Таким образом расчеты показали, что в кривых радиусом 349-300 м существует возможность после проведения дополнительных исследований устанавливать ширину колеи 1525 мм вместо 1530 мм, чтобы иметь большой запас на уширение колеи с учетом допустимой величины бокового износа рельсов.
- Теоретические исследования динамического вписывания грузовых вагонов в кривые с использованием методики А.Я. Когана учитывающей коничность колес, нелинейную зависимость сил и моментов трения от относительного скольжения колес по рельсам, жесткости в сочленениях тележки при набегании гребня колеса на боковую поверхность рельса показали, что направляющие силы и полюсные расстояния имеют существенную зависимость от непогашенных ускорений и некоторую зависимость от радиуса кривых. Наиболее тесную зависимость от радиуса кривой имеет угол набегания гребня колеса на боковую грань рельса.
На внутреннюю рельсовую нить при свободном вписывании тележек модели 18-100 в кривых передается только сила трения от поперечного скольжения колес по рельсам.
Обобщение полученных данных при вычислительном эксперименте по модели А.Я. Когана, а также результатов расчета по методике О.П. Ершкова, учитывающей продольные силы в поезде, и экспериментальных данных позволили получить приближенные зависимости направляющих, боковых сил и полюсных расстояний от непогашенного ускорения, радиуса кривой, вертикальных колесных нагрузок и продольных сил в поезде.
- В результате экспериментальных исследований на опытных участках Западно-Сибирской железной дороги с использованием видеокамер установлено, что при движении вагонных тележек по кривым радиусом менее 650 м реализуется свободное вписывание с обязательным контактом между гребнем первого по ходу колеса и наружным рельсом.
Между гребнями колес и внутренним рельсом при ширине колеи в пределах 1520… 1540 мм всегда фиксируются зазоры, величина которых зависит от ширины колеи и ширины колесной пары (колесной колеи). Следов касания гребнями, внутренних нитей не отмечено.
- Ширина вагонной колесной пары в расчетном уровне (колесная колея) в соответствии с существующими нормами может изменяться в пределах от 1511 до 1489 мм. Ширина колеи в месте установки приборов в кривой радиусом 407 м равнялось 1539 мм. В этом случае зазор в колее мог находиться в пределах 28…50 мм. Фактически по результатам расшифровки видеокадров он находился в пределах 35…50. Для второй оси зазор между гребнем колеса и боковой гранью внутреннего рельса находился в пределах 5…45 мм. Касание гребней колес рабочей грани внутреннего рельса не зафиксировано.
Углы набегания гребней колес вагонов на наружный рельс составляли 0,351,1°. Величина их определяется радиусом кривых, непогашенным поперечным ускорением, силами трения, возникающими в подпятнике тележки и между поверхностями катания колес и рельсов, коничностью колес. Влияние ширины колеи на этот процесс не отмечено.
В кривой радиусом 625 м отмечено виляние первой, набегающей на наружный рельс, колесной пары с отрывом гребня колеса от боковой грани наружного рельса.
6. Боковой износ наружного рельса сопровождается образованием полки с углом наклона 30…32°, по которой начинают катиться локомотивные и вагонные колеса с отрывом поверхности катания колес от рельса. Расчеты показывают, что для удержания колес с вертикальной нагрузкой 115 кН на полке с углом наклона 31° достаточно боковых сил величиной 35…55 кН.
Качение переднего колеса гребнем по наклонной выработке в головке рельса вызывает сильный перекос вагонной тележки с образованием больших зазоров между гребнем заднего колеса и боковой гранью наружного рельса.
Список Литературы
- Богданов В.М. Снижение интенсивности износа гребней колес и бокового износа рельсов / Ж.д. транспорт, 1992, №2. С. 30-34.
- Холодецкий А.А, Исследование влияния внешних сил на верхнее строение железнодорожного пути // Инженер. 1896. № 12. С. 507-517.
- Хейман X. Направление железнодорожных экипажей рельсовой колеи / Пер. с нем. Под ред. К П. Королева. М.: Трансжелдориздат. 1957- 416 с.
- Uebelacker G. Untersuchunden über die Bewegung von Lokomotiven mil Drehgestellen in Bahnkrümmungen. Beilage zum. Organ f.d.F.E. 1903, S. 1-26,
- Цеглинский К.Ю. Железнодорожный путь в кривых. M., 1903- 155 с.
- Козийчук П.Г., Королев К.И. Об унификации ширины колеи в прямых и кривых участках пути // Техника железных дорог. 1948. № 11. С. 14 – 17.
- Фришман М.А. Исследование взаимодействуя пути и подвижное состава методом киносъемки. М.: Трансжелдориздат, 1953. 116 с.
- Ершков О.П., Мелентьев Л.П., Яхов М.С. Расчеты железнодорожного пути в кривых и нормы его устройства. М.: Трансжелдориздат, 1960. 205 с.
- Birmann F. Schienenriffelen, ihre Erforschun gund Verhütung. VDJ Zeitschrift. 1958. 100. № 30. 1453-1462. 38.
- Gerlach A., Köhler M.; Beckedahl H.; Hothan J.: Zur Eignung des Schotteroberbaues für die Neubaustrecken der Deutschen Bundesbahn, Mitteilungen aus dem Fachgebiet Konstruktiver Straßenbau im Institut für Verkehrswirtschaft, Straßen-wesen und Städtebau der Universität Hannover, Heft 10, 1989.
- Tilting Trains (Pendolino), Perseverance brings commercial reward, Railway Journal 12/1992.
- Fastenrath, Fritz.: Die Eisenbahnsehiene, Verlag von Wilhelm Ernst & Sohn, Berlin, München, Düsseldorf 1977.
- Prud’homme, M. A.; Janin M. G.: Die Stabilität des mit durchgehend geschweißten Schienen veriegten Gleises, Revue Générale des Chemins de Fer 2/1968.
- Führer, Gunther: Oberbauberechnung, transpress, VEB Verlag für Verkehrswesen, Berlin, April 1978.
- Schramm: Oberbautechnik und Oberauwirtschaft, O. Eisner Verlag Ges., Darmstadt 1973.
- Keim Dieter: Theoretische Untersuchung der Eigenfrquenzen und Schwingungsamplituden bei schotterlosen Oberbaukonstruktionen und klassischem Schotteroberbau, ETR Eisenbahntechnische Rundschau (25) 1/1976, S. 94ff.
- Bergander В.: Rechnerische Untersuchungen des Schwingverhaltens von Schienenfahrzeugen in senkrechter Richtung, Indenieur Arhiv (32), 1977.
- Katoh Y.; Kakegawa H.: Effects of Runner-pad under Concrete Tie on Pulverization or Ballast, Vibration and Noise; Quarterly Reports Railway Research Institute, Japanes National Railways, Vol. 18, (1977), №1.
- ORE 117: Das rheologische Verhalten des Oberbaus, Report 4, April 1974.
- Lätsch R.: ZusammenhangFederzahl des Gleises und der Schienenunterstützung, ZEV+DET Glasers Annalen 5/1976.
- Alias J.; Colson F.; Fortin J.-R; Fourcade J.: Le traitment des défauts de surface du rail; Revue Générale des Chemins de Fer (97) 3/1978, S. 164-183.
- Schneider E.: Ein Beitrag zur Erforschung des dynamischen Verhaltens des Schotteroberbaues bei Eisenbahnen: Mitteilungen des Instituts für Bau von Landesverkehrswegen der Technischen Universität München, Heft 20, München 1974.
- Правила технической эксплуатации железных дорог Российской федерации / ЦРБ-756. МПС РФ. – М.: Трансжелдориздат, 2000. 190 с.
- Инструкция по текущему содержанию железнодорожного пути / ЦП-774. МПС РФ. – М.: Трансжелдориздат, 2000. 223 с.
- Шахунянц Г.М. Железнодорожный путь. М.: Трансжелдориздат, 1961.
615с. - Справочник инженера-путейца / Под ред. В.В. Басилова и М.А. Чернышева. М.: Транспорт, 1972. Т. 1. 768 с.
- Ершков О.П. Построение графиков удельных характеристик и графиков- паспортов вписывания железнодорожных экипажей в кривые (теоретические основы). – Тр. ВНИИЖТа, 1963, вып. 268. – С. 64-125.
- Ершков О.П. Расчет поперечных горизонтальных сил в кривых. М.: Транспорт, 1966. 235 с.
- Коган А .Я., Левинзон М.А. Теоретические исследования влияния различных эксплуатационных факторов на износ рельсов, гребней и бандажей колесных пар – М: ВИНИТИ, 1996. Деп. № 6054, 119 с.
- Коган А .Я. Оценка износа рельсов и бандажей колесных пар при движении подвижного состава в кривых участках пути / Вестник ВНИИЖТ, №2, 1990, С. 36-40.
- Зак М.Г. Влияние моментов трения в опорных устройствах грузового вагона на допускаемые скорости движения в кривых // Скорости движения поездов в кривых: Сб. науч. тр.: М., 1988. С. 20 – 25.
- Вершинский C.B., Данаков В.И., Хусидов В.Д. Динамика вагона // Под ред. C.B. Вершинского. М.: Транспорт, 1991. – 360 с.
- Лысюк B.C. Путейское обеспечение эксплуатации тяжеловесных и длинносоставных поездов. М.: 1987. — 94 с.
- Ершков О.П., Зак М.Г. Расчеты вписывания в кривые грузового вагона на тележках ЦНИИ-ХЗ с учетом продольных сил // Повышение прочности и надежности пути: Сб. науч. тр. М.: Транспорт, 1989. С. 59-65.
- Вершинский C.B. Устойчивость вагонов от выжимания продольными силами при торможении // Динамика, прочность и устойчивость вагонов в тяжеловесных и скоростных поездах: Сб. науч. тр. М.: Транспорт, 1970. С. 4-39.
- Зак М.Г., Ершков О.П., Ткачев Е.Д. Теоретический анализ влияния расстройств рельсовой колеи на динамическое взаимодействие подвижного состава и пути и оценка неравножесткости рельсовых нитей // Исследование накопления расстройств рельсовой колеи железнодорожного пути: Сб. науч. тр. М.: Транспорт,
- С. 67-102.
- Железнодорожный путь и подвижной состав для высоких скоростей движения // Под ред. М.А. Чернышева. М.: Транспорт, 1964. 272 с.
- Ершков О.П., Крепкогорский С.С., Зак М.Г. Повышение скоростей движения поездов по кривым участкам пути // Исследование возможности повышения скоростей движения поездов. – М.: Транспорт, 2002. 128 с.
- Коган А.Я., Шестаков В.Н., Коваль В.А. Воздействие на путь поездов повышенной массы на перевальных участках Львовской железной дороги // Повышение прочности и надежности пути: Сб. науч. Тр. М.: Транспорт, 1989.С. 5059.
- Ромен Ю.С. , Коваль В.А., Левинзон М.А. Взаимодействие пути и грузовых вагонов при движении тяжеловесных длинносоставных поездов // Подвижной состав и путь в условиях интенсификации работы железных дорог: Сб. науч. Тр. М.: Транспорт, 1989, с. 20-29.
- Карпущенко Н.И., Котова И.А. Анализ факторов, определяющих износ рельсов в кривых малого радиуса / Сборник докладов научно-практической конференции «Современные проблемы взаимодействия подвижного состава и пути. Колесо – рельс 2003». М., 2003. – С. 101-105 (всего 192 с).