Цикл статей:
Глава 1 — Ударное взаимодействие колеса и рельса
Глава 2 — Исходные уравнения и характеристики
Глава 3 — Аналитические решения задач взаимодействия колеса и рельса
Глава 4 — Численные алгоритмы расчетов
Глава 5 — Результаты расчетов и сравнение с экспериментом
Сравнение параметров удара по различным моделям
Построенный численный алгоритм позволяет находить решение поставленной задачи для различных моделей динамического поведения рельса, как балки на упругом основании. После решения большого числа примеров утвердилось априорное мнение о том, что модель С.П. Тимошенко дает наиболее достоверные результаты.
На рис. 5.1 показаны результаты определения силовых и кинематических параметров удара для трех рассмотренных моделей поведения балки на упругом основании. Как видно из графиков на рис. 5.1, для контактной силы, перемещения и изгибающего момента результаты для сравниваемых моделей мало отличаются. Это было подмечено Г.Б. Муравским [87], построившим импульсную переходную функцию для рассматриваемой задачи. Что касается ускорений, то для них заметен вклад деформаций сдвига, отсутствующих в классических моделях. Особо стоит подчеркнуть, что перемещения и ускорения, определяемые в точке удара (z=0) на основе моделей Эйлера и Рэлея, не затухают во времени. Требуется обязательно вводить диссипативные силы. При этом можно воспользоваться теорией Е.С. Сорокина [100]. В модели С.П. Тимошенко затухание обеспечивается влиянием упругого основания.
На рис. 5.2. показан характер затухания максимальных значений параметров удара вдоль оси рельса по мере удаления от точки удара. Как видим, затухание всех параметров удара вдоль оси балки обеспечивается без учета диссипативных сил.
На рис. 5.4 и 5.5. показаны спектральные плотности параметров ударного процесса. Пиковое значение частоты 250 Гц соответствует граничной частоте балки, лежащей на упругом основании с погонным коэффициентом постели 160 МПа.
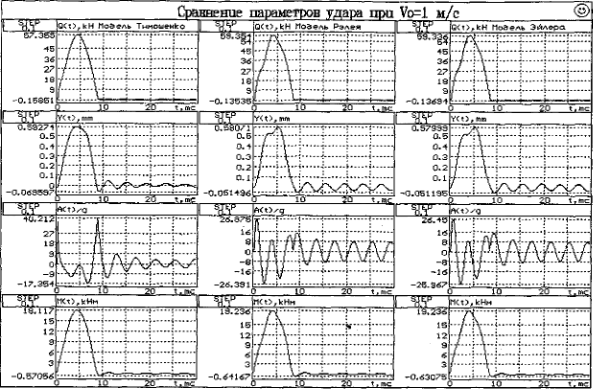
Рис. 5.1. Сравнение параметров удара по трем динамическим моделям для рельса
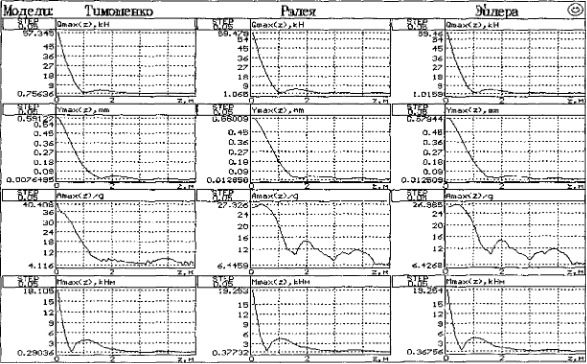
Рис. 5.2. Затухание максимальных значений параметров удара по длине рельса
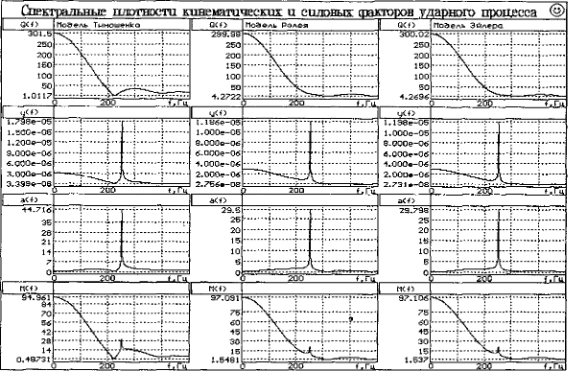
Рис. 5.3. Спектральные плотности функций, характеризующих ударный процесс в точке г=0
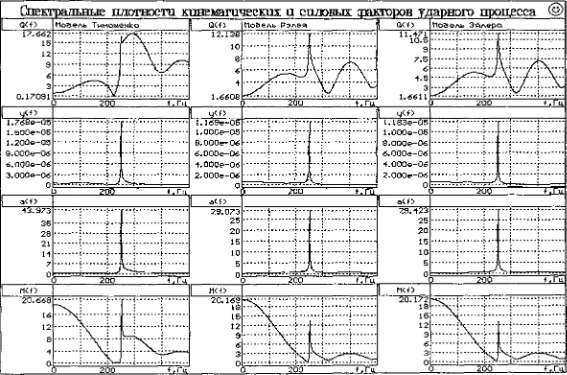
Рис. 5.4. Спектральные плотности функций, характеризующих ударный процесс в точке г=1 м
Сравнение результатов расчета с данными экспериментов
В ноябре 1998 г. в депо «Сокол» Московского метрополитена при непосредственном участии автора [43] были проведены натурные измерения ускорений рельса при прохождении состава, имевшего одну колесную пару с предельно-допустимым ползуном глубиной 4.5 мм. В табл. 5.1. приведены основные характеристики колеса и рельса.
| Таблица 5.1. | Буквенное 1 | Числовое | |
| Наименование | обозначение | Размерность | значение |
| Тип рельса | Р-43 | — | — |
| Масса колеса | М | кг | 600 |
| Радиус колеса | Я | мм | 400 |
| Глубина ползуна | ъ. | мм | 4.5 |
| Хорда ползуна | ь | мм | 120 |
| Нагрузка на колесо | в | кг | 7000 |
| Жесткость основания | и | МПа | 230 |
| Контактная жесткость | Ко | Н*мА(-3/2) | 1.2*10+п |
Для записи ускорений использовались акселерометры с пьезокристаллами. Датчики были установлены на внутреннем скосе подошвы рельса в четырех сечениях с шагом 0.5 метра. Запись показаний датчиков велась в течение 5 сек, с шагом по времени 0.001 сек. Скорость движения состава в условиях депо не могла быть большой, она составила 5 и 8.9 км/ч. Было выполнено 4 рейса, записан большой объем информации. С помощью аналого-цифрового преобразователя информация в виде числовых файлов сохранялась в памяти порта
тивного персонального компьютера. При тарировке датчиков был учтен наклон рельса на основании и уклон скоса подошвы рельса.
Для обработки данных эксперимента автором была составлена специальная программа на языке С++, которая позволяет делать выборки из массивов данных и при необходимости дифференцировать или интегрировать по времени необходимое число раз законы изменения интересующих параметров.
На рис. 5.5. в качестве наглядного примера приведены графики ускорений, записанные при выполнении рейса N4. Выборка (правые графики; отсчет времени смещен на 3.932 с) дает более детальное описание процесса удара колесной пары в четырех сечениях рельса. Судя по максимальным амплитудам, удар по рельсу пришелся между вторым и третьим датчиками.
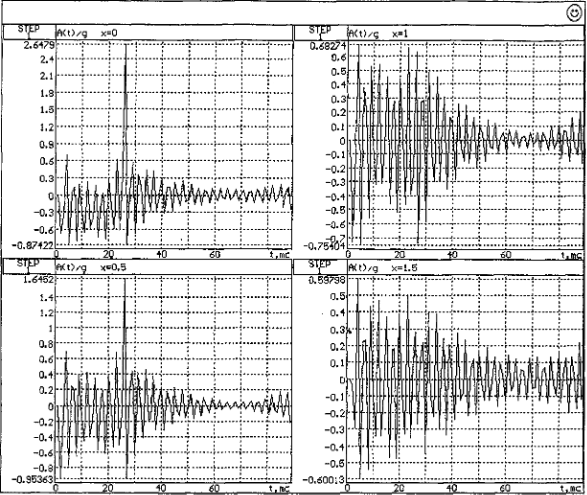
На рис. 5.6. приведены расчетные графики изменения ускорений в четырех сечениях рельса. Расчет проведен при тех же исходных данных. Как видно, общий характер расчетных графиков ускорений удовлетворительно согласуется с их экспериментальными аналогами. Шаг вычислений был принят равным половине шага записи показаний датчиков — 0.0005 с.
Следует отметить, что на расчетные значения ускорений существенное влияние оказывает шаг по времени; возможен пропуск максимальных значений ускорений. Аналогичное явление происходит и при экспериментальной записи. Поэтому для более достоверного сопоставления с данными эксперимента желательно уменьшить шаг записи показаний датчиков.
Кроме обработки данных собственного эксперимента, проведено сопоставление расчета с опытами других авторов: H.H. Кудрявцева [58] и П.С. Ани- симова [5]. Основные исходные данные приведены в табл. 5.2. На рис. 5.7 показаны результаты расчета ускорений колеса для двух конкретных примеров.
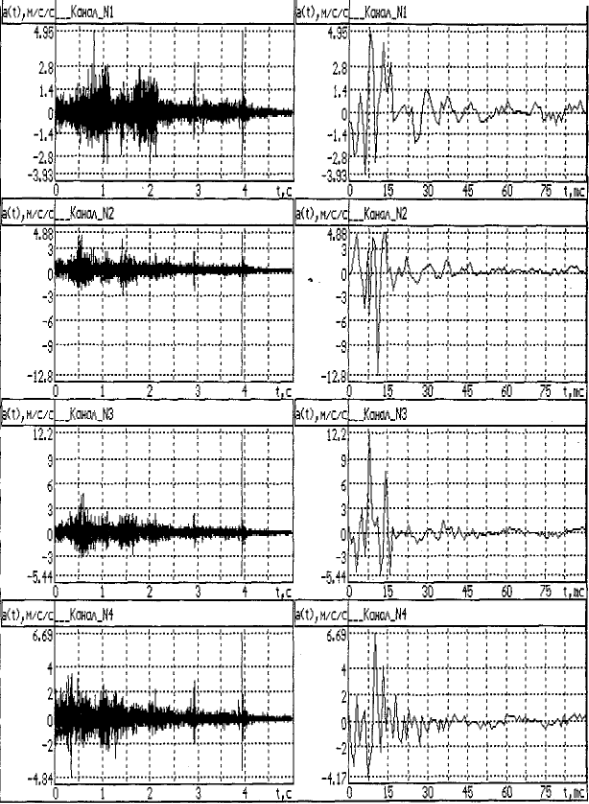
Рис. 5.5. Экспериментальные акселерограммы
| Таблица 5.2.Наименование параметров | Числовые значения в примерах | |
| Н.Н. Кудрявцева | П.С. Анисимова | |
| Тип рельса | Р-65 | Р-50 |
| Масса колеса, кг | 630 | 630 |
| Радиус колеса, мм | 450 | 475 |
| Нагрузка на колесо, кг | 3200 | 4500 |
| Глубина ползуна, мм | 1.5 | 2.0 |
| Жесткость основания, МСЗа | 160 | 160 |
| Контактная жесткость, Нм «15 | 1.0*10″ | 9.8*1010 |
Влияние различных параметров на дополнительное напряженное состояние при ударах
Максимальные параметры напряженно-деформированного состояния при ударе наблюдаются при определенном значении скорости поезда, когда происходит «обезгрузка» колеса, т.е. давление на рельс равно нулю. В приводимых примерах для скорости поезда принималось (если не оговорено другое) именно такое значение.
В одной из работ, выполненных на кафедре, рассмотрен вопрос об эффективности сглаживания хорды ползуна. На рис. 5.8. приведен пример расчета с учетом этого обстоятельства. Параметром сглаживания служит отношение центральных углов введенной с целью сглаживания дуги и той дуги, которая отвечает имевшемуся ползуну. Радиус вводимой дуги меньше радиуса колеса и вычисляется по специальной формуле.
Еще более опасная ситуация (по сравнению с наличием ползуна) возникает при наличии на колесе навара. С ростом скорости движения поезда интенсивность первого ударного процесса непрерывно растет, никакой обезгрузки не происходит. При вторичном ударе возможна обезгрузка, т.к. колесо «падает » с некоторого возвышения.
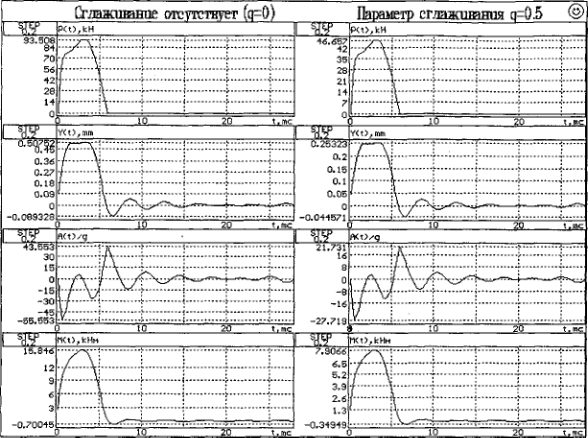
Рис 5.8. Эффективность сглаживания хорды ползуна
На рис. 5.10. показаны результаты решения конкретного примера для тройного удара колеса по рельсу. Первый удар вызван наличием на ободе колеса ползуна, второй и третий — наличием навара. Исходные данные соответствуют рельсу Р-65, типовому колесу грузового вагона (R=0.475 м, т=620 кг, нагрузка на колесо 9712 кг). Глубина ползуна и навара принята равной 2 мм.
На рис.5.11. показана зависимость максимальных значений параметров удара от важнейших исходных характеристик: жесткости основания (погонного коэффициента постели) Ux, начальной скорости удара V0 , контактной жесткости Kq.
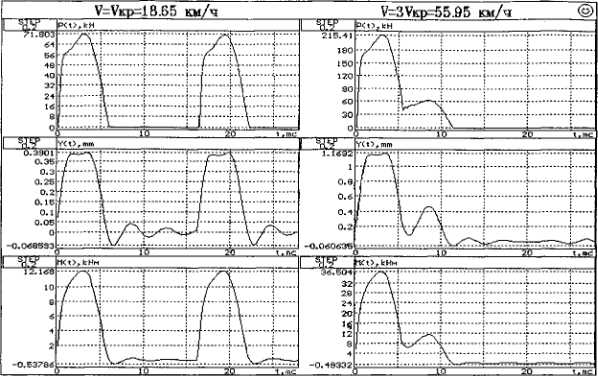
Рис. 5.9. Влияние скорости поезда на параметры двойного удара колеса с наваром
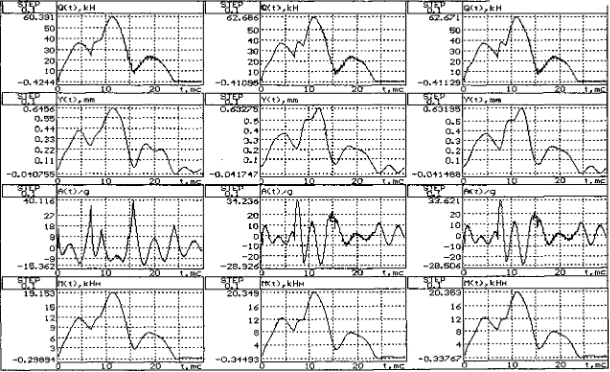
Рис. 5.11. Характер влияния исходных данных на параметры ударного процесса
Следует обратить внимание на почти линейную зависимость параметров от значения начальной скорости удара. Это позволяет прогнозировать результаты решения многих задач через одно эталонное решение при фиксированной скорости. Нестабильное поведение графиков, особенно для Атах(их) можно объяснить недостаточной точностью численного дифференцирования и выбранным шагом вычислений по переменной Их. Уменьшение этого шага привело к некоторому сглаживанию графиков.
В заключение можно утверждать, что построенный метод расчета и его программное обеспечение позволяют более достоверно решать задачу удара массивного тела по балке на упругом основании при варьировании в широких пределах всех исходных данных.
Основное напряженное состояние рельса при равномерном качении колесного экипажа
Теоретические результаты, описанные в параграфе З.5., наглядно иллюстрируется нижеследующими примерами. На рис. 5.12. показаны в зависимости от продольной координаты эпюры прогибов, изгибающих моментов и поперечных сил, возникающих в сечении рельса при равномерном качении колесной пары, не имеющей дефектов. Эти графики отнесены к подвижной системе координат, начало которой совпадает с точкой контакта колеса с рельсом.
Рассмотрим влияние деформаций сдвига на прогибы рельса под колесом. Прогибы, определяемые в соответствии с исходным уравнением (3.11) для модели С.П. Тимошенко по выражению (3.13), имеют такие максимальные значения:Если деформации сдвига не учитываются, то максимальные прогибы выражаются более простой формулой [2].
Полная картина напряженно-деформированного состояния
Для получения полной картины напряженно-деформированного состояния в сечении рельса под точкой контакта необходимо параметры основного состояния, возникающего при равномерном качении колесной пары, сложить с дополнительными, возникающими от ударного действия колесной пары при наличии ползунов.Внутренние силовые факторы основного напряженного состояния и прогибы оси рельса определяются выражениями (3.13-3.15). При вычислении нормальных напряжений в сечении под силой могут быть также учтены местные напряжения.
Таблица 5.3. Прогибы рельса под колесом (в мм) и их отношение
| Жесткость U, МПа | Р-50 | Р-65 | Р-75 | ||||||
| УТ | УЭ | f | ут | УЭ | f | Ут | УЭ | f | |
| 30 | 3.00 | 2.90 | 1.036 | 2.62 | 2.52 | 1.036 | 2/46 | 2.37 | 1.035 |
| 50 | 2.07 | 1.98 | 1.047 | 1.80 | 1.72 | 1.046 | 1.69 | 1.62 | 1.044 |
| 70 | 1.62 | 1.54 | 1.055 | 1.41 | 1.34 | 1.055 | 1.32 | 1.26 | 1.052 |
| 90 | 1.35 | 1.27 | 1.062 | 1.18 | 1.11 | 1.062 | 1.10 | 1.04 | 1.059 |
| 110 | 1.17 | 1.09 | 1.069 | 1.02 | 0.95 | 1.068 | 0.95 | 0.90 | 1.066 |
| 130 | 1.04 | 0.97 | 1.075 | 0.90 | 0.84 | 1.074 | 0.85 | 0.79 | 1.071 |
| 150 | 0.94 | 0.87 | 1.080 | 0.81 | 0.75 | 1.079 | 0.76 | 0.71 | 1.076 |
| 170 | 0.86 | 0.79 | 1.085 | 0.75 | 0.69 | 1.085 | 0.70 | 0.65 | 1.081 |
| 190 | 0.79 | 0.73 | 1.090 | 0.69 | 0.63 | 1.089 | 0.65 | 0.59 | 1.086 |
| 210 | 0.74 | 0.67 | 1.095 | 0.64 | 0.59 | 1.094 | 0.60 | 0.55 | 1.096 |
| 230 | 0.69 | 0.63 | 1.099 | 0.60 | 0.55 | 1.098 | 0.56 | 0.52 | 1.094 |
| 250 | 0.65 | 0.59 | 1.103 | 0.57 | 0.51 | 1.102 | 0.53 | 0.48 | 1.098 |
| 270 | 0.62 | 0.56 | 1.107 | 0.54 | 0.49 | 1.106 | 0.50 | 0.46 | 1.102 |
| 290 | 0.59 | 0.53 | 1.111 | 0.51 | 0.46 | 1.110 | 0.48 | 0.43 | 1.105 |
| 310 | 0.56 | 0.50 | 1.114 | 0.49 | 0.44 | 1.113 | 0.46 | 0.41 | 1.109 |
| 330 | 0.54 | 0.48 | 1.118 | 0.47 | 0.42 | 1.117 | 0.44 | 0.39 | 1.112 |
Здесь индексом «0» отмечены параметры, относящиеся к основному состоянию, индексом «1» — параметры ударного происхождения. Индекс «Ь» принят для местных нормальных напряжений. На рис. 5.13. показан вид эпюр напряжений в сечении под колесом. В табл. 5.4 и 5.5 приведены исходные данные и числовые результаты проведенных расчетов.
На рис. 5.13 показан характер эпюр напряжений в сечении под колесом. Крайняя правая эпюра отражает распределение нормальных напряжений в горизонтальных площадках сечения рельса. Величина стх, является контактным напряжением в малой окрестности точки соударения. Величина стх2 дает представление о порядке внутренних напряжений сжатия в точке, находящейся ниже головки рельса в самом начале его стенки.

Рис. 5.13. Эпюры напряжений в поперечном сечении рельса (качественная картина; пунктиром показана нейтральная ось)
В табл. 5.5. напряжения в крайних волокнах рельса даны в виде дроби: в числителе — без учета местных напряжений, в знаменателе — с учетом. Знак минус принят для растяжения. Как видно из данных табл. 5.5, местные напряжения дают ощутимую поправку; дополнительные напряжения, возникающие при ударе, существенно увеличивают суммарное напряжение.
Таблица 5.4. Исходные данные к числовому примеру расчета
| Буквенное | Числовое | ||
| Наименование | обозначение | Размерность | значение |
| Тип рельса | Р-65 | — | — |
| Масса колеса | mk | кг | 620 |
| Радиус колеса | R | м | 0.475 |
| Нагрузка на колесо | G | кг | 9712 |
| Динамический коэффициент | Dk | — | 1 |
| Жесткость основания | ux « | МПа | 160 |
| Размеры площадки контакта | b(l)*LP | мм* мм | 10*8 |
| Контактная жесткость | Ко | Нм ~3/2 | 1.2Е+11 |
Заключение
Выполнено теоретическое исследование специальной задачи динамики сооружений — ударного взаимодействия массивного тела с континуальной одномерной средой.
Несмотря на логическую завершенность работы, она может быть продолжена по двум направлениям. Во-первых, результаты могут быть использованы заинтересованными службами и организациями для проведения практических расчетов.
Во-вторых, целесообразно дальнейшее развитие в теоретическом отношении. Могут быть уточнены модельные представления о колесе; в общих чертах ясен порядок рассмотрения пространственных изгибно-крутильных деформаций рельса от ударов при наличии относа и виляния колесной пары.
Исходная более полная система дифференциальных уравнений имеется (она приведена в главе 2); преобразование по Лапласу для нахождения реакции рельса выполнено. Значения крутильной жесткости рельса, без которых решение нельзя довести до числа, найдены. Однако необходимость раскрытия определителя высокого порядка существенно усложняет задачу, численный алгоритм должен начаться раньше, его построение, отладка и реализация потребуют определенных усилий.
Заманчиво было бы учесть стохастический характер некоторых параметров, влияющих на решение задачи. Прежде всего это относится к параметрам жесткости упругого основания. Но все это далеко выходит за рамки одной диссертации.
По работе могут быть сделаны следующие основные выводы
- Предложен метод расчетной оценки дополнительного напряженно- деформированного состояния в рельсах от ударов колесных пар на стыках, а также при наличии дефектов в виде ползунов или навара. Построенный метод и его программное обеспечение позволяют решать задачу удара массивного тела по балке на упругом основании при варьировании в широких пределах всех исходных данных.
- На базе решения вспомогательных задач (начальная скорость удара, контактная жесткость) необходимые для расчета исходные данные уточнены. Возможности предложенного метода проиллюстрированы достаточным количеством примеров.
- Дополнительное напряженно-деформированное состояние сопоставлено с основным, найденным с учетом деформаций сдвига. Учтены также местные напряжения в зоне удара. Важность полученного результата состоит в том, что дополнительные напряжения могут в несколько раз превышать основные, не связанные с ударами.
- Достоверность полученных результатов подтверждена близостью результатов, полученных по различным моделям, а также данными экспериментов (проведенных при участии автора, а также другими исследователями).
- Полученные результаты и отлаженные программы могут быть использованы в практических расчетах, нацеленных на уточнение ограничений в части эксплуатации подвижного состава с дефектными колесными парами.
Используемая Литература
- Александров A.B., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов. — М.: Высшая школа, 1995. — 560 е.: ил.
- Анисимов П.С. Взаимодействие колеса с ползуном и рельса // Вестник ВНИИЖТ. 1963. №1. с.42-47.
- Сорокин Е.С. К теории внутреннего трения при колебаниях упругих систем. М.: Госстройиздат. 1960. — 120 с.
- Муравский Г.Б. Колебания бесконечной балки Тимошенко на упругом основании. — Строительная механика и расчет сооружений, МИИТ, 1979, №6, с. 56-61.