Цикл статей:
Глава 1 – Вибродиагностика подшипников грузовых вагонов Глава 2 – Математическая модель вибраций колесной пары и буксового узла при наличии дефектов
Глава 3 – Функционирование математической модели на пвм
Глава 4 – Компьютерная диагностика неисправностей подшипников
Исходные дифференциальные уравнения задачи
Математическая модель любого динамического объекта содержит: расчетную схему в выбранной системе координат; зависимости деформаций от перемещений и реакций от деформаций; уравнения равновесия и процедуру их исследования.
Расчетная схема колесной пары, установленной на стенде, может быть представлена упругим круглым стержнем, который через ролики опирается на наружные и внутренние кольца, затем на корпуса букс и на основание (см.рис.2.1).
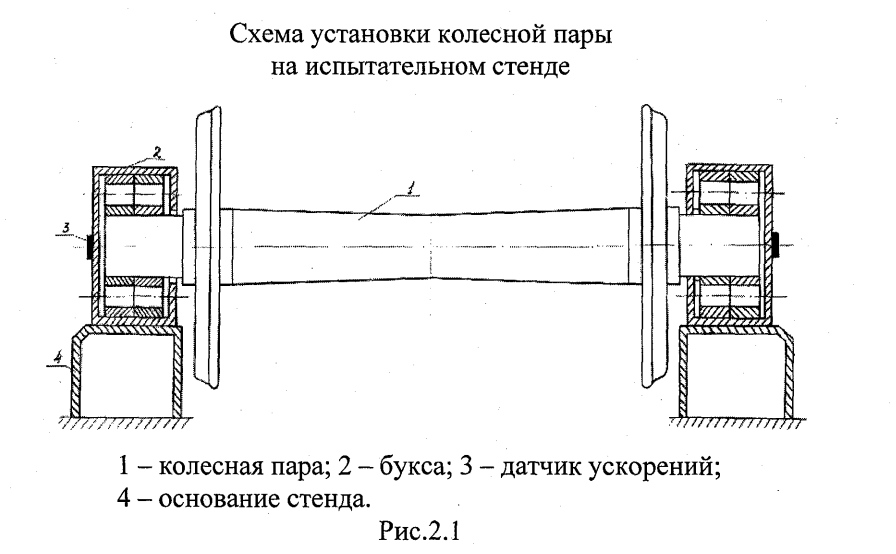
Предполагаем, что при вращении колесной пары с дефектными подшипниками возбуждаются изгибные колебания оси и вертикальные колебания корпусов букс.




Дискретизация расчетной схемы колебаний колесной пары на
стенде. Преобразование дифференциальных уравнений в
частных производных в обыкновенные дифференциальные
уравнения
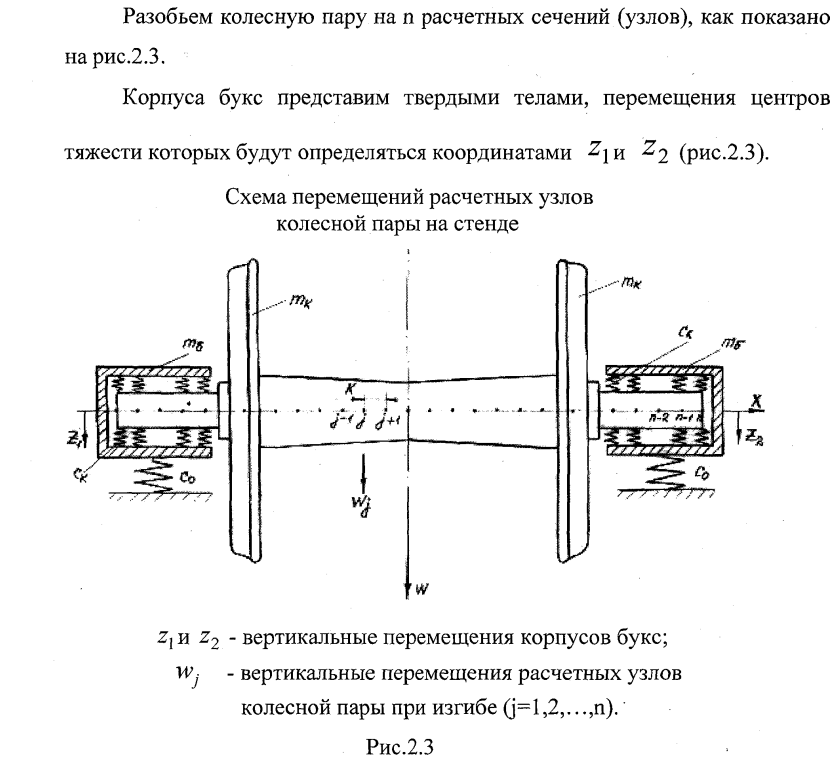

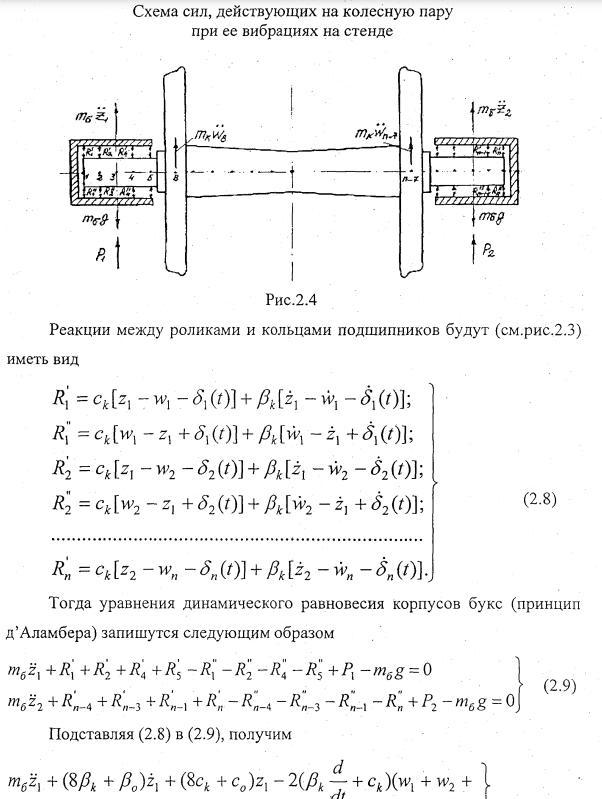





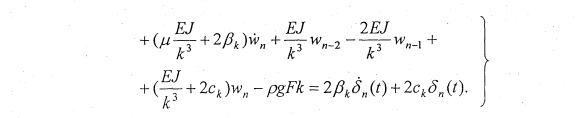
Таким образом, мы получили систему n+2 обыкновенных дифференциальных уравнений, которыми описываются изгибные колебания колесной пары на стенде от воздействия дефектов подшипников.
Векторно-матричный вид дифференциальных уравнений математической модели «стенд-колесная пара»
Систему дифференциальных уравнений (2.17) можно представить в векторно-матричном виде.
Введем вектор состояния системы, компонентами которого будут являться все координаты, т.е.

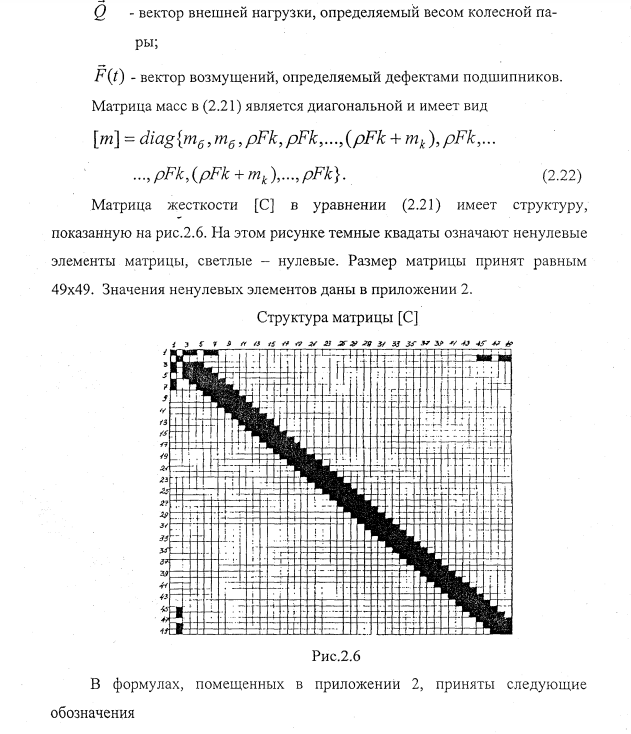


Расчетные методы, используемые при компьютерном моделировании динамики стенда
К расчетным методам, используемым в диссертации при анализе динамики стенда и колесной пары, относятся: метод численного интегрирования и нахождение собственных чисел и собственных векторов. Дифференциальные уравнения, описывающие колебания расчетной схемы стенда и колесной пары, представлены в векторно-матричном виде (2.21).
Эта система дифференциальных уравнений является математической моделью динамического процесса. Интегрирование этой системы дифференциальных уравнений на ЭВМ представляет процедуру цифрового моделирования колебаний колесной пары на стенде.
Метод численного интегрирования дифференциальных
уравнений
При проведении данных исследований к методу интегрирования предъявлялось два основных требования. Это возможность интегрировать дифференциальные уравнения, в которых порядок старшей производной равен двум (как в обычных уравнениях д’Аламбера) и по возможности большое быстродействие, которое определяется количеством вычислений правой части уравнения на одном шаге интегрирования.
В научной школе, сложившейся на кафедре «Вагоны и вагонное хозяйство» МИИТ’а, в течение многих лет в задачах динамики использовался разностно-итерационный способ интегрирования дифференциальных уравнений, предложенный профессором В.Д.Хусидовым [54].
Суть его заключается в следующем.
Если имеем векторную форму дифференциального уравнения (2.21), приведенную к нормальной форме Коши в виде
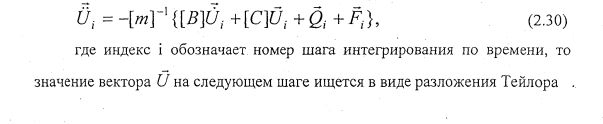

Если при проведении m итераций условие (2.35) не выполняется, то шаг интегрирования уменьшается (например, делится пополам) и вычисления по формулам (2.34), (2.30) и (2.35) производятся с уменьшенным шагом. Таким образом, изложенный метод интегрирования не требует понижения порядка старшей производной до единицы (как это предусмотрено в большинстве традиционных методов), работает с автоматическим выбором шага h в зависимости от заданной точности £ . Он достаточно хорошо апробирован в исследованиях многих авторов [15,35,47,55]. Недостатком этого метода является то, что при интегрировании систем высокого порядка возрастает время вычислений на ЭВМ.


Вычисление собственных значений системы



Возмущения динамической модели, определяемые дефектами подшипников
В процессе эксплуатации в подшипниках вагонных букс возникает большое количество повреждений, не связанных с их полным разрушением, но нарушающих нормальную работу и представляющих угрозу безопасности движения [27,33].
К наиболее распространенным дефектам относятся:
- раковины на дорожках качения наружных и внутренних колец;
- раковины на поверхности роликов;
- шелушение на поверхностях колец и роликов;
- трещины в кольцах и роликах подшипника;
- электроожоги на поверхностях колец и роликов;
- вмятины на дорожках качения колец и на роликах, а также большое количество монтажных повреждений и повреждений, вызванных коррозией рабочих поверхностей подшипников.
Для предложенной в диссертации математической модели указанные повреждения являются внешними возмущениями, которые имеют кинематический характер.
По виду повреждений эти возмущения могут иметь гармонический или импульсно-периодический характер.
Для аналитического описания функций возмущений необходимо задаться их формами, амплитудами и частотами.
Вообще говоря, любую периодическую функцию можно представить рядом Фурье, в котором удерживается один или несколько членов.
В простейшем виде импульс внешнего периодического возмущения может быть представлен функцией вида


Выводы по главе 2
- Для практического создания компьютерной системы диагностирования дефектов подшипников разработана математическая модель вибрации колесной пары на стенде.
- Математическая модель описывает упругие колебания оси колесной пары с учетом инерционных свойств колес, насаженных на ось, корпусов букс, упругих свойств оси, роликов в зоне их контакта с кольцами и упругих свойств основания стенда.
- В дифференциальных уравнениях вибраций системы «колесная пара-стенд» учитываются диссипативные свойства в материале оси и роликов, а также в основании стенда, которые приняты в соответствии с гипотезой Фойхта.
- В исходном виде математическая модель вибраций системы «колесная пара-стенд» представляет собой многоточечную граничную задачу для дифференциальных уравнений в частных производных. Для исследования такой задачи использован метод дискретизации, позволивший перейти от дифференциального уравнения в частных производных к системе обыкновенных дифференциальных уравнений, в которых на стадии дискретизации учтены граничные условия, определяемые опиранием колесной пары через подшипники и буксы на стенд.
- Предложен способ определения начальных условий интегрирования, которые представляют собой начальные статические перемещения расчетных сечений колесной пары на стенде.
- При вычислении собственных значений системы, для симметризации матрицы разрешающих уравнений, использован метод вращения векторов, предложенный Якоби.
- Вычисление собственных частот колебаний позволило определить верхнюю границу шага интегрирования дифференциальных уравнений модели и частотный диапазон, в котором необходимо производить измерения.
Список литературы
- Бидерман B.JI. Прикладная теория механических колебаний. М.. «Высшая школа», 1972, 416 с.
- Биргер И.А. Техническая диагностика. М., «Машиностроение». 1978,239 с.
- Вершинский C.B., Данилов В.Н., Хусидов В.Д. Динамика вагона. Под ред. С.В.Вершинского. М., «Транспорт», 1991, 360 с.
- Вериго М.Ф., Коган А .Я. Взаимодействие пути и подвижного сос-тава. Под ред. М.Ф.Вериго. М., «Транспорт», 1986, 560 с.
- Вериго М.Ф., Петров Г.И., Хусидов В.В. Имитационное моделиро-вание сил взаимодействия экипажа и пути. Бюллетень ОСЖД, Варшава, N6, 1995, с. 3-8.
- Вибрации в технике. Справочник, т.З. Под ред. Ф.М.Диментберга и К.С.Колесникова. М., «Машиностроение», 1980, 544 с.
- Вибрации в технике. Справочник, т.5. Под ред. М.Д.Генкина. М., «Машиностроение», 1981, 496 с.
- Гантмахер Ф.Р. Лекции по аналитической механике. М., «Наука», 1966, 300 с.
- Ден-Гартог Дж. Механические колебания. Пер. с англ. М., «Фи- зматгиз», 1960, 580 с.
- Гарг В.К., Дуккипати Р.В. Динамика подвижного состава. Пер. с англ. М., «Транспорт», 1988, 391 с.
- Годфри Д. Теория упругости и пластичности. Пер. с англ. Под ред. П.М.Варвака, Киев, «Будевильник>>, 1969, 309 с.
- Данилов В.Н. Железнодорожный путь и его взаимодействие с под-вижным составом. М., «Трансжелдориздат», 1961, 111 с.
- Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М., «Физматгиз», 1963, 400 с.
- Евсеев Д.Г., Медведев Б.М., Ципкин Б.С. Способ диагностики подшипников. A.C. 1552092А1, Бюл.Ш1, 1990, Госкомитет по изобретениям и открытиям.
- Золотарский А.Ф., Вершинский C.B. и др. Железнодорожный путь и подвижной состав для высоких скоростей движения. М., «Транспорт», 1964, 272 с.