Напряженное состояние рельсовой плети и методы его определения

Оглавление

Цикл статей:
Глава 1 – Напряженное состояние рельсовой плети и методы его определения

Глава 2 – Исследование факторов, влияющих на формирование продольных сил в плети

Глава 3 – Метод определения напряженного состояния плети

Глава 4 – Автоматизированная система контроля напряженного состояния плетей бесстыкового пути

Введение

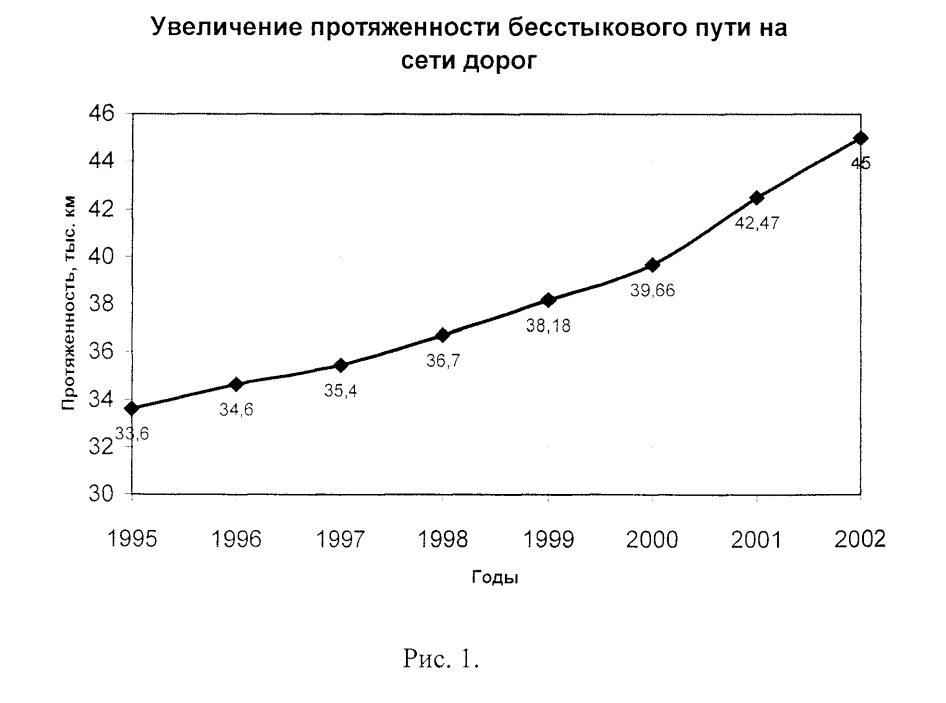
Один из путей снижения эксплуатационных расходов на содержание пути это расширение полигона укладки бесстыкового пути, который имеет ряд преимуществ по сравнению со звеньевым. Это прежде всего снижение затрат на содержание стыков. Эти затраты на звеньевом пути составляют до 80% эксплуатационных расходов. Снижается сопротивление движению подвижного состава на 8-12%, увеличивается плавность хода. Чем больше на дороге протяженность бесстыкового пути, тем меньше на ней возникает отказов рельсов по ряду опасных дефектов. Число поперечных изломов рельсов в бесстыковом пути примерно в 4 раза меньше, чем в звеньевом. Рельсы в бесстыковом пути до их замены пропускают тоннаж на 10% больше, чем в звеньевом. Интенсивность бокового износа в кривых в бесстыковом пути меньше, чем в звеньевом. В настоящее время протяженность бесстыкового пути составляет более 42 тыс. км, это 34 % от развернутой длины главных путей рис. 1. На многих зарубежных дорогах эта цифра составляет от 60 до 90%. Такое различие связано с рядом особенностей отечественных железных дорог:

наличие регионов с годовым перепадом температуры 115 °С, и более;
конструктивные особенности скреплений, не позволяющие обеспечить равномерное по длине плети и одинаковое во времени прижатие рельса к подкладкам и подкладок к шпалам;
несовершенство механизма контроля соблюдения требований действующих технических указаний на бесстыковой путь, как в процессе укладки, так и при эксплуатации.

Опыт эксплуатации бесстыкового пути показывает, что значительная часть выбросов происходит из-за несоблюдения норм и требований технических указаний на бесстыковой путь.

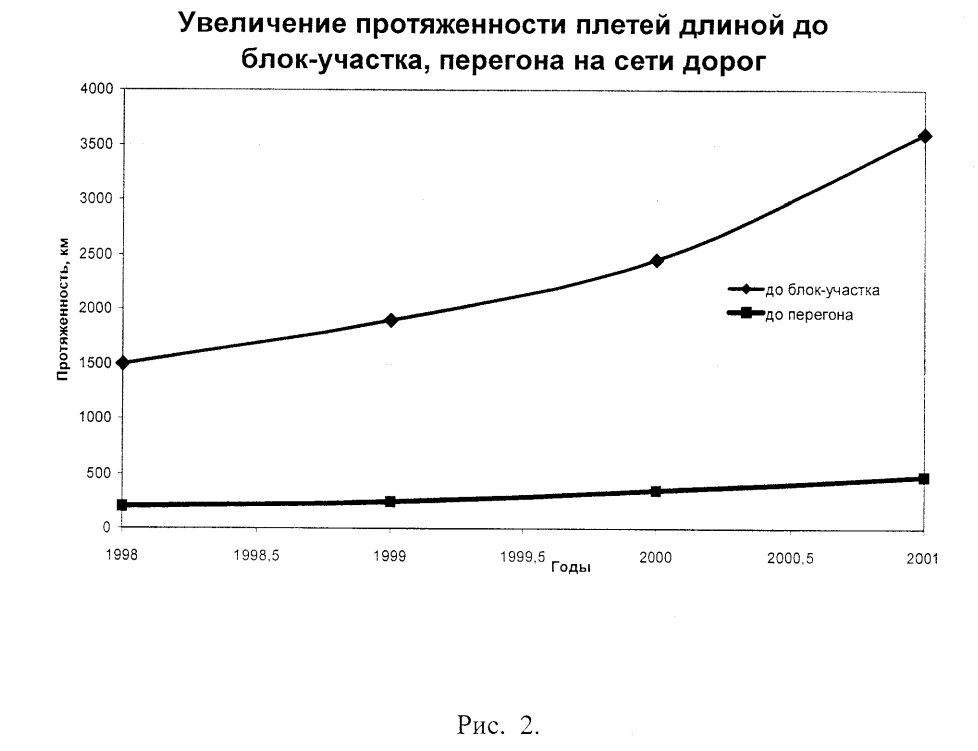
Бесстыковой путь предъявляет дополнительные требования к технологии укладки и текущего содержания. Основное требование это обеспечение должного температурного режима при укладке и контроль его изменения в процессе эксплуатации. Перечисленные причины не позволяют обеспечить постоянство температурного режима бесстыкового пути в процессе эксплуатации. Поэтому необходимы средства диагностики температурного режима плетей, их продольно-напряженного состояния, для того чтобы своевременно принять меры по разрядке напряжений. Такая диагностика особенно актуальна, когда плети достигают длины блок-участка, перегона, и в условиях, когда используется вваривание в плети стрелочных переводов и применение тональной автоблокировки. Протяженность бесстыкового пути с плетями длиной до перегона постоянно увеличивается (см. рис. 2) и составляет 480 км.

С ростом длины плетей возрастет неравномерность распределения продольных напряжений по их длине. Это вызвано рядом факторов, среди которых:

неравномерное закрепление при укладке,
неравномерность свойств балласта и геометрии балластной призмы,

разность температуры закрепления коротких плетей сваренных в длинную,

различные условия эксплуатации в плане и профиле,
ремонтные работы на отдельных участках плети,
наличие участков, восстановленных сваркой с предварительным изгибом,
угон рельсошпальной решетки, угон плетей.

Эти факторы или их сочетание могут стать причиной концентрации продольных напряжений на отдельных участках плети, что может привести к выбросу пути летом и излому плети зимой. Распределение этих факторов по длине плети и во времени имеет случайный характер. В этих условиях возникает необходимость контролировать продольно-напряженное состояние бесстыкового пути.

На основании анализа сходов отнесенных на выброс пути с 1995 по 1999 г.г. получено:

среднее время задержки в движении поездов при выбросе пути -10 ч.;
средняя протяженность поврежденного при выбросе пути – 171,6 м;
среднее число поврежденных до исключения единиц подвижного состава

при выбросе пути – 7.

Эти данные еще раз говорят о необходимости создания средств диагностики напряженного состояния бесстыкового пути.

Вопросами устойчивости бесстыкового пути занимались отечественные ученые Альбрехт В.Г., Ангелейко В.И., Боченков М.С., Бромберг Е.М., Вериго М.Ф., Виногоров Н.П., Грищенко В.А., Ершков О.П., Ершов В.В., Зверев Н.Б., Клинов С.И., Коган А .Я., Крейнис З.Л., Маркарьян М.А.., Мищенко К.Н.,Морозов С.И., Новакович В.И., Першин С.П., Путря H.H., Членов Т.С., Чирков Н.С., Шахунянц Г.М. и другие. За рубежом исследованиями устойчивости бесстыкового пути занимались Ваттман И., Майер Г., Рааб Ф., Амман О., Грюнвельдт С., Бирман Ф., Немешди Е., Немчик Я., Надь И., Нумат М., Сакмауер Л., Леви Р., Мартине А. и другие.

При всем многообразии имеющихся моделей и методов расчета устойчивости бесстыкового пути, до настоящего времени не существует общепризнанного метода, следовательно, нет оценки устойчивости его различных эксплуатационных состояний при отступлениях от норм содержания. Известно достаточно много приборов и методик для контроля температурного режима, но до сих пор наиболее доступным и распространенным является контроль по маячным шпалам [106]. Трудоемкость этого метода и отсутствие наглядной картины распределения по всей длине плети резко снижают его эффективность. Достаточно часто качество нанесения меток возле маячных шпал сводит к нулю возможность контроля по ним температурного режима рельсовых плетей бесстыкового пути. В то же самое время ведутся активные работы по усовершенствованию систем диагностики пути, в частности, путеизмерителей системы ЦНИИ-2 и ЦНИИ-4. Предлагается ввести в качестве дополнительного параметра состояния пути – продольно- напряженное состояние плетей. Для этого путеизмерительные вагоны оборудуются соответствующей диагностической системой.

Следует отметить, что в действующих технических указаниях по устройству, укладке, содержанию и ремонту бесстыкового пути (ТУ) [106] заложены достаточные коэффициенты запаса по устойчивости против выброса при соблюдении установленных норм и требований. Однако далеко не всегда эти нормы и требования соблюдаются. Поэтому для диагностики бесстыкового пути предлагается контролировать не только текущее продольно-напряженное состояние, но и проверять соблюдение норм и требований действующих ТУ. Для этого необходимо создание электронной базы данных по бесстыковому пути, а так же механизма ее заполнения и проверки.

Анализ методов и средств определения напряженного состояния плетей бесстыкового пути

Анализ технических средств для контроля напряженного состояния рельсовых плетей

Работы по созданию средств диагностики напряженного состояния бесстыковых рельсовых плетей проводятся несколько десятилетий и продолжаются. Сложность проблемы объясняется тем, что бесстыковая рельсовая плеть – несущая конструкция, работающая в непосредственном контакте с другими элементами верхнего строения пути и подвижного состава. В процессе эксплуатации она меняет свои параметры под воздействием подвижного состава, окружающей среды, и других факторов. Эти и другие причины вызывают значительные трудности при разработке средств диагностики продольно-напряженного состояния бесстыкового пути.

Многолетняя практика и исследования выделили, как единственно целесообразный, температурно-напряженный вариант бесстыкового пути, в котором четко определена зависимость между действующими продольными силами и колебаниями температуры. Для этого температурно-напряженный бесстыковой путь должен быть надежно закреплен на основании. Такое требование предусматривается действующими Техническими указаниями по устройству, укладке, содержанию и ремонту бесстыкового пути (ТУ) [106]. В этом случае все продольные усилия в рельсовых плетях заранее прогнозируются расчетами и определяются перепадами температур по сравнению с температурой закрепления плетей. Поэтому, для оценки фактических продольных сил (напряжений) в нормально содержащемся пути достаточно измерять фактические температуры рельсов, что не представляет технических трудностей. Однако, вследствие неравномерного ослабления закрепления плетей бесстыкового пути, разрыхления балластной призмы при проведении ремонтных работ без последующего необходимого уплотнения, нарушений технологий ремонтных работ и т.д., создаются участки возможных местных продольных деформаций плетей и участки без деформаций, служащие как бы неподвижными упорами. Перед этими упорами продольные силы, возникающие при равномерном движении и/или торможении поездов, создают сжимающие напряжения в плетях, а за упорами – растягивающие. В режиме набора тяги происходит обратное явление. Величины продольных сил, а также длины, местонахождение и степень закрепления «свободных» и «упорных» участков неизвестны и непостоянны. Напряженное состояние плетей в этих условиях определяется уже не только температурными изменениями, а некоторой суммой силовых воздействий, прогнозировать которую практически невозможно. А соответственно и нельзя с высокой степенью точности говорить о фактическом напряженном состоянии плетей бесстыкового пути.

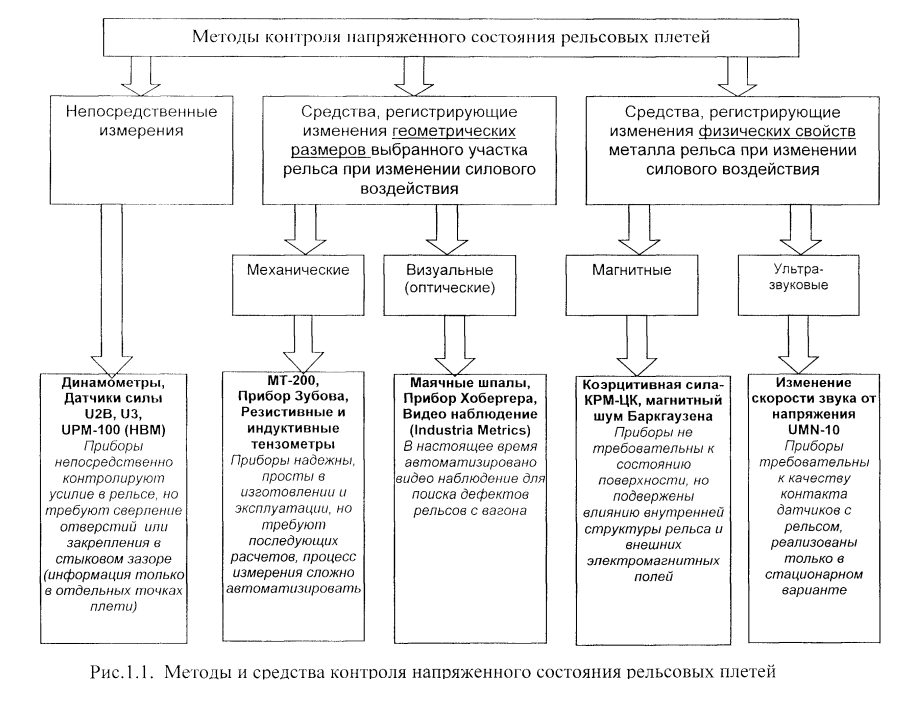
В работе [50] описано устройство, использующее прогиб части плети, закрепленной в двух точках и нагруженной сосредоточенной вертикальной силой как меру продольной силы в плети. При этом требуется полное раскрепление исследуемого участка плети, что неприемлемо для диагностики действующего пути. Известны методы контроля напряженного состояния плетей по качеству нанесенных на ее поверхностей лаков, по частоте колебания вибрационных датчиков в виде струны [33] и другие. Но далеко не все методы можно применить для диагностики напряженного состояния плетей действующего пути. Для того чтобы знать напряженное состояние плетей, вне зависимости от качества содержания пути, необходимы надежные и простые средства специального контроля непосредственно в пути за накоплением «эксплуатационных» остаточных продольных сил (напряжений) в рельсовых плетях. Обзор некоторых способов контроля продольных напряжений в плетях выполнен Н.Б. Зверевым [40]. Эти способы по принципу действия можно разделить на несколько групп (см. рис. 1.1.)

Оптические способы

В Германии [39] был разработан оптико-механический деформометр, который измеряет в одном месте рельса продольную и поперечную деформацию по меткам, нанесенным на предварительно очищенную подошву рельса. Деформации определяются с помощью микроскопа. Этот прибор имеет ряд конструктивных недостатков, однако его применение вполне возможно в лабораторных условиях.

В 1983 г. сотрудники ДИИТа А.Г. Иванов и Н.И. Смуров предложили “Бесконтактный оптический способ измерения остаточного угона пути”. Его суть в использовании визирного луча трубы отслужившего срок геодезического инструмента. Трубу крепят на опоре контактной сети или другом неподвижном устройстве поперек оси пути. На рельсах делают метки, по которым через трубу определяют продольные смещения плетей. Позже в комплект аппаратуры добавили электронные детали (фоторезисторы), и система стала автоматической. Появилась возможность фиксировать деформации рельсов под поездами. Однако из-за несовершенства система не получила распространения, тем более, что она не вскрывает фактического напряженного состояния плетей, а делает попытку определить напряжение вызванное воздействием на плети дополнительных силовых факторов (поездная нагрузка, путевые машины и т.д.)

Достоинства оптических способов – это их относительная простота и наглядность, к недостаткам можно отнести сложность автоматизации процесса измерений.

Механические способы

механический тензометр МТ-200. Имея базу 20 см и рычажную передачу деформаций рельсов на индикатор (мессуру) с соотношением плеч 1:5, он измеряет удлинения или укорочения базы (расстояния между двумя метками — кернами — на наружной грани головки плети) с точность 0,002 мм (цена деления мессуры — 0,01 мм), что соответствует примерно 2,1 МПа. Это равносильно нагреву или охлаждению закрепленного рельса приблизительно на 1°С. С учетом возможных помех и погрешностей в полевых условиях можно считать реально достижимой точность измерений прибором МТ-200 в пределах 2,5—5,0 МПа, что соответствует изменению температуры рельсов на 1—2°С. В процентном отношении такая точность вполне приемлема, если учесть, что практически напряжения могут достигать 250—300 МПа (2500—3000 кгс/см ). Диапазон измерений МТ-200 достаточен.

Прибор простой конструкции, изготавливается из легко доступных материалов (корпус — из рельсовой стали, индикатор — стандартная мессура с ходом ножки 10 мм, термометр — типовой бытовой малогабаритный с ценой деления 1°С). Его можно сделать в любых механических мастерских. Размеры прибора 22x10x2 см, масса 1 кг. Ножки (одна — неподвижная, другая — на шарнире) со сферическими окончаниями, что обеспечивает четкую центровку в конических кернах на головке рельсов. Термометр связан “термически” с корпусом для учета температурных деформаций самого прибора.

В 80-х годах опытный завод ВНИИЖТа изготовил механический тензометр ИПН, в основу которого заложен стандартный микрометр. База измерений 140 мм. Цена деления эквивалентна 2,5 МПа. Для устранения влияния на показания прибора температурных деформаций самого прибора рабочая часть его изготовлена из инвара. Прибор дороже МТ-200 из-за применения микрометра, его устанавливать в местах измерений сложнее.

Еще в 1977 г. в ЦНИИ МПС H.A. Карпов разработал механический прибор на базе путевого шаблона ЦУП. Вместо штанг для измерения ширины колеи применены две встречные штанги: одна — подвижная с пружиной и рукояткой (рычагом), другая — неподвижно соединенная с корпусом шаблона. Наружные концы штанг имеют сферические окончания и колодочки для опирания на башмаки в пазухе рельсовой плети. Башмаки изготовлены из того же типа металла, что и плеть, у них по два болтовых отверстия, сквозь которые и через шейку рельса проходят болты, стягивающие башмаки с двух сторон шейки. Для предотвращения возможных сдвижек башмаки дополнительно вклеены в пазухи и расположены так, что расстояния в свету между гранями, в которые упираются концы штанг при измерениях, равны 2100 мм. Это сделано потому, что измерительная база (аналогично кернам в МТ-200), равная 2100 мм, — начальная длина и, если начальные напряжения (ст₀ равны 0, то при изменениях базы (во время нагрева, охлаждения или угона и т.п.) каждое деление шкалы прибора, равное 0,1 мм, будет соответствовать “круглой” величине а = 10 кгс/см^– (1 МПа). Значения б пропорциональны модулю упругости стали Е – 2,1 ТО ~^б кгс/см². Для учета возможных температурных деформаций на его корпусе установлен малогабаритный термометр (как и в МТ-200). В транспортном положении прибор складывается.

В 80-х годах в Венгрии применили механический прибор “Деформометр НИИЖТ ВНР” для определения действительной нейтральной температуры плетей. Прибор подобен рассмотренным, но имеет конструктивные отличия. Например, напряжения не определяются, а сразу показывается изменение начальной температуры плети: 1₀ = 1°С при удлинении (укорочении) линейки прибора на 0,01 мм. Точность измерений = ±2°С. Линейка изготовлена из инвара (кроме короткого конца, где крепится мессура). База прибора равна 870 мм.

В Германии изготовлен прибор, аналогичный МТ-200, но с двойной системой ножек (на обе стороны рельса, с кернами на верху подошвы). Его предлагали в 80-х годах внедрить в России. Вместо индикаторов использованы линейные нониусы с микроскопами для чтения показаний. Цена деления — 1 Мпа. база — 300 мм. Немецкие специалисты назвали свой прибор оптико- механическим (из-за упомянутого микроскопа). Существенное отличие от МТ- 200 заключается в измерении одновременно с продольными и поперечных деформаций. Подошва рельсов в поперечном направлении — свободный стержень, и при нагреве или охлаждении изменяет размеры точно пропорционально изменениям температуры. Между продольными и поперечными деформациями существуют определенные зависимости. В данном приборе измерения обрабатываются с учетом этого по довольно сложным формулам.

К механическим способам можно отнести способ, рекомендованный в 1983 г. В.А. Межелайтисом для оценки изменений продольных напряжений в плетях в кривых при работе тяжелых путевых машин по изменениям проектной стрелы кривой. Указывается, что искажение начального температурно-напряженного состояния бесстыкового пути при работе этих машин в 80 % случаев равно 18— 20 °С.

В Венгрии, кроме упомянутого деформометра, в кривых при работе машин и в других случаях, также предложен способ, сходный с предыдущим: измеряют стрелы, пересчитывают их в продольные силы и “нейтральные” температуры.

Прибор ПЗ-20 (автор В.И. Зубов) отличается от описанных принципиально. Он передвижной — собран на однорельсовой трехосной тележке (две оси связаны жестко, третья — соединена с передней тележкой шарнирно). Рабочий орган ролик — колесо, катящееся по рельсу. Во избежание проскальзывания по головке рельса ролик изготовлен из феррита и на заводе намагничен. Диаметр ролика 100 мм, зубчатой передачей он связан со счетчиком оборотов. В РСП с большой точностью на верхе подошвы плетей в процессе их сварки наносят керны диаметром 2 мм через каждые 20000 ±0,5 мм. После укладки и в процессе эксплуатации ПЗ-20 прокатывают по всей плети (или даже по нескольким плетям) вручную, и у каждого керна на подошве делают отсчет по горизонтальному диску счетчика. По разнице отсчетов между отдельными проездами ПЗ-20 на базовых 20-метровых отрезках пути определяют, как и при переносных приборах, изменения продольных напряжений.

Данный способ, наряду с достоинствами (высокая производительность) имеет и недостатки предыдущих способов: необходимость в паспортизации, получение данных в неявном виде, т.е. с обработкой и т.д. Кроме того, это достаточно сложный механизм, требующий заводских условий изготовления, наладок и регулировки. Он тяжелый, прокатывается раздельно по левой и правой нитям, поверхность рельсов должна быть сухой.

Недостаток всех механических способов – сложность автоматизации процесса измерений и потребность в начальной (исходной) базе измерений.

Магнитные способы

В его основе — свойство намагниченных материалов иметь разную магнитную проницаемость по сечению в зависимости от степени сжатия или растяжения. Практически оно сводится к созданию в рельсе магнитного поля и сравнению намагниченности отдельных мест по сравнению с ненагруженным участком (эталоном). Возможна и работа без эталона (дифференциальный метод): в рельсовой плети магнитное поле наводят двумя соленоидами, а активные датчики располагают крестообразно под углом к активным соленоидам. Магнитные силовые линии образуют равноплечий симметричный “швейцарский крест”. При приложении механической нагрузки (продольные силы в рельсе) симметрия нарушается, и в активных датчиках возникает разница ЭДС (электродвижущих сил), пропорциональная изменению нагрузки.

Недостаток способа – зависимость магнитной проницаемости не только от механических напряжений, но и от структуры металла, намагниченности рельсовых нитей сигнальными и тяговыми токами и др. Необходима ”паспортизация” измерительных точек, т.е. предварительное установление “начальных” магнитных характеристик данной точки рельса и последующем получение разницы отсчетов в любой момент с начальными данными, что ограничивает возможности магнитной тензометрии. Другими словами, для того чтобы провести измерение необходимо знать предыдущее состояние. Достоинство — независимость от чистоты поверхности в местах измерения, не нужны керны, риски и другие “порчи” поверхности, в перспективе — возможность дистанционной работы (из вагона и т.п.) при помощи электро- и радиосвязи с использованием компьютерных сетей и т.д.

На магнитном принципе основаны приборы, созданные в последние десятилетия в России и за рубежом: ПИОН — прибор для определения остаточных напряжений (автор Н.Н.Максимов, 1970 г.), ИСОН — измеритель статических остаточных напряжений (Н.Ф.Врублевский, 1991 г.), прибор Свердловского “ПромстройНИИПроекта” (Т.Х.Бекташев, 1983 г.), прибор Японских Национальных железных дорог (1989 г.), прибор AREA (США, 1982 г.). Эти и аналогичные приборы имеют названные недостатки и пока не получили широкого применения на пути.

Известен метод магнитного шума, основанный на эффекте Баркгаузена, который заключается в том, что намагничивание и размагничивание металла рельса идет по гистерезисному циклу не путем равномерного изменения их намагниченности, а скачками, которые и получили название скачков Баркгаузена. Ферромагнитные ^материалы при отсутствии магнитного поля состоят из областей спонтанного намагничивания (доменов), каждая из которых намагничена практически до насыщения. Векторы намагниченности этих областей направлены вдоль так называемых направлений легкого намагничивания. При намагничивании и перемагничивании происходит поворот доменов ферромагнетика по направлению вектора напряженности внешнего магнитного поля. Из-за неоднородности материала процесс изменения границ доменов может происходить только если будет преодолен некоторый энергетический уровень-барьер и при этом проявляется характерный электромагнитный шум, причем его параметры связаны с дефектами материала ферромагнетика.

На этом же эффекте основан прибор RailScan, разработанный Венгерской фирмой METALELEKTRO, результатом измерений которого является распределение нейтральной температуры вдоль изхмеряемого рельса. Конструктивно прибор выполнен в виде однорельсовой тележки. В нижней части расположены датчики, а на пружинной скобе, в верхней части расположен электронный блок с дисплеем, на котором, можно наблюдать распределение нейтральной температуры по длине плети в виде графика. Вместе с тем имеется отечественный аналог этого прибора – ИНТРОМАТ [96], представленный фирмой РКК, который имеет большие функциональные возможности, но конструктивно не адаптирован для контроля рельсовых плетей. Во ВНИИЖТ с участием автора совместно с фирмой РКК были проведены лабораторные испытания прибора ИНТРОМАТ [96]. Испытания показали, что прибор пригоден для контроля продольных напряжений рельсах, но в полевых условиях на действующей линии испытания не проводились. Целесообразно было бы проведение совместных полевых испытаний приборов RailScan, ИНТРОМАТ, и по возможности других, с целью определения пригодности их для практического использования, в пути.

МНПО «СПЕКТР» и фирма СНР разработали прибор «Магнитный структуроскоп КРМ-ЦК» [100] с преобразователем на постоянном магните. Анализ результатов пробных путевых испытаний прибора КРМ-ЦК с автономным питанием показывает, что прибор на внешние электрические воздействия не реагирует, хорошо отражает общую картину работы бесстыкового пути в кривых участках пути, но имеет нестабильность показаний, поэтому дальнейшая обработка результатов не проводилась. Прибор КРМ-ЦК хорошо «различает» сырые и объемнозакаленные рельсы, что может расширить его область применения.

Фирмой “Энергодиагностика’* разработан Индикатор концентрации напряжений ИКН-1М для диагностики напряженно-деформированного состояния оборудования и конструкций с использованием метода магнитной памяти металла. Прибор не требует предварительного намагничивания контролируемых объектов, так как используется остаточная намагниченность, сформировавшаяся в процессе их эксплуатации. Прибор компактный, легкий, имеется возможность передачи данных на компьютер. Применение этого прибора для контроля напряженно-деформированного состояния рельсовой плети затруднено наличием различных магнитных полей в зоне измерения.

Московской фирмой РКК представлен индикатор механического напряжения ИН-1 [98], предназначенный для измерения деформаций и внутренних напряжений в нагруженных элементах конструкций и сооружений. Принцип работы прибора основан на преобразовании деформаций конструкций, возникающих вследствие приложения к ним различного вида нагрузок в механические колебания рабочего элемента датчика.

Основной недостаток – на результаты измерений влияет не только напряженное состояние рельса, но и его внутренняя структура (дефекты), а также дополнительные магнитные поля, так как рельс является проводником тягового тока и сигнальных токов автоблокировки плюс наводки от контактного провода. Кроме того, этот способ требует нулевой базы, от начальных промеров при а,=0, что требует паспортизации плетей, то есть тарировку приборов во всех точках, где будут проводиться измерения.

Ультразвуковые способы

Принцип действия ультразвуковых приборов основан на изменении скорости прохождения звука через материал при изменении механической нагрузки (напряжения): чем больше механическое напряжение, тем больше скорость прохождения звука между двумя контрольными точками. Известен японский прибор [93] (1982 г.) имеет датчик с пьезокристаллическими преобразователями. Особый счетчик измеряет время прохождения пропускаемого сигнала между искательными головками, расположенными на фиксированном расстоянии. Для исключения помех от наклепа, износа и других дефектов сигнал вводится в головку рельса под углом. Точность измерений — приемлемая, но широкому использованию прибора мешает его сложность, хрупкость, высокая чувствительность к состоянию поверхности контакта.

Прибор ДЭБРО (Польша, 1986 г.) сходен с предыдущим, но имеет головку, вводящую акустический сигнал в шейку рельса. Как и предыдущий прибор, он может давать точные показания, но чувствителен к качеству поверхности контакта. В 1996 г. во ВНИИЖТе проводились испытания Ультразвукового тензометра [100]. В процессе испытаний были установлены значения чувствительности – не хуже 0,02 кг/мм”. Испытания позволили установить ряд недостатков, которые не позволяют рекомендовать прибор для массового применения.

Прибор ЦМЫ-Ю, разработан в Польше во Вроцлавском политехническом институте в 80-х – 90-х годах, основан на использовании ультразвуковых волн. Принцип действия основывался на том, что при изменении механических напряжений в металле, скорость прохождения ультразвуковых волн изменяется (акустоу пру гость или акустоанизотропия). В лабораторных условиях приборы показывали хорошие результаты, однако, широкого практического применения, по причинам указанным выше, они не нашли [110, 87].

В США предпринималась попытка применить акустоупругий эффект [114]. Был разработан ультразвуковой зонд, который генерирует и принимает продольную волну, параллельную оси рельсов. Зонд рассчитан на базу измерений 216 мм. Измерение абсолютных значений напряжений (суммы собственных, эксплуатационных, температурных и др.) данным способом затруднено. Возможно измерение лишь относительных напряжений, а для этого обязательна паспортизация рельсов и начальные отсчеты при отсутствии напряжений.

В Акустическом институте рассмотрен вариант акустического метода оценки продольного сжатия рельсов при их тепловом расширении. Суть метода в том, что величина усилия продольного сжатия оценивается не по зондированию ультразвуком в вертикальной плоскости методом дефектоскопии, а по изменению скорости распространения низкочастотных звуковых волн вдоль рельса. Это позволяет уменьшить влияние структуры металла и выработки рельса. Метод реализован посредством акустических согласующих конструкций в виде специальных клиньев, прижимаемых к рельсу и измерении разности фаз между излученным и принятым сигналами. База измерения 100 м, частота сигнала 10 кГц, мощность сигнала менее ватта. Основное достоинство этого метода в том, что скорость распространения сигнала не зависит от трещин (от трещин зависит только затухание сигнала). Недостаток метода в необходимости жесткого контакта зондов с рельсом, что усложняет процесс автоматизации измерений. Общий недостаток акустических методов – влияние внутренней структуры рельса на измерение напряженного состояния и повышенные требования к контакту зонда с рельсом, а так же потребность в паспортизации плетей и обязательные начальные отсчеты при а,=0.

Анализ расчетных методов и программных средств определения устойчивости бесстыкового пути и напряженного состояния плетей

Достаточно полный обзор методов расчета устойчивости бесстыкового пути выполнен Вериго М.Ф. [23]. В нем автор отмечает, что в каждом из этих методов сделаны различные по форме и значимости упрощающие расчетную схему допущения, приняты разные степени детализации, различные предположения о форме деформаций рельсов в плане после их выброса, имеются различия в методах составления исходных уравнений и т. п. По этим причинам даже при отсутствии различия принимаемых в расчетах параметров конечные результаты, полученные с учетом этих методов, существенно различались друг от друга, и от результатов, полученных в специально поставленных опытах [15, 23].

В работе [89] С. П. Першиным дан глубокий анализ различных методов, опубликованных до 1962 г. В нем автор отмечает, что во всех ранее применявшихся расчетных схемах для исследования устойчивости бес стыкового пути в основу положена расчетная схема статического равновесия рельсо-шпальной решетки под действием продольных температурных сжимающих сил и сил, сопротивляющихся ее сдвигу; эта статическая расчетная схема не позволяет математически описать и определить кинетику процесса выброса бесстыкового пути.

В работе А. Я. Когана «Продольные силы и перемещения бесстыкового пути» [51] впервые задача устойчивости пути решаются с использованием теории случайных функций. В этой работе изложены общие положения теории продольных сил и перемещений в бесстыковом пути, возникающих при воздействии на него температурных и других продольных сил, дано решение задачи построения продольных сил и перемещений пути как случайных функций длины в форме характеристических функционалов, изложены результаты некоторых экспериментальных исследований по определению расчетных параметров и др.

Работа А. Я. Когана содержит исследование устойчивости железнодорожного пути в нелинейной постановке при действии на рельсы пассивной реактивной тангенциальной и нормальной нагрузок и распределенного момента от взаимодействия рельсовых плетей со скреплениями. В ней дан не только общий метод составления дифференциального уравнения статического равновесия бесстыкового пути, но и, что весьма важно, разработан математически более точный метод учета разрядки продольных сил в рельсах, возникающих при этом поперечных сдвижках рельсо-шпальной решетки и рассмотрены вопросы повторного нагружения пути температурными силами.

Энергетические методы

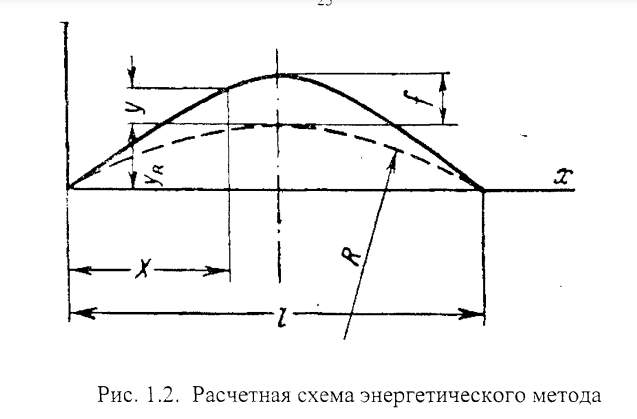
Энергетический метод [89] состоит в определении условий равновесия изогнутого стержня. При искривлении упругого стержня его потенциальная энергия уменьшается вследствие удлинения его оси и зависит от параметров искривления, то есть от стрелы/и хорды / рис. 1.2.

Методы дифференциальных уравнений

В работе [89] отмечено, что составление и решение дифференциальных уравнений равновесия дают возможность ликвидировать основной недостаток энергетических методов: уравнения упругой линии при этом вытекают из принятых условий нагружения. Расчетная схема метода дифференциальных уравнений изображена на рис. 1.3. Метод дифференциальных уравнений использовал М.А. Мартине [65]. Для изгибающего момента М_х, действующего в сечении х справедливо уравнение

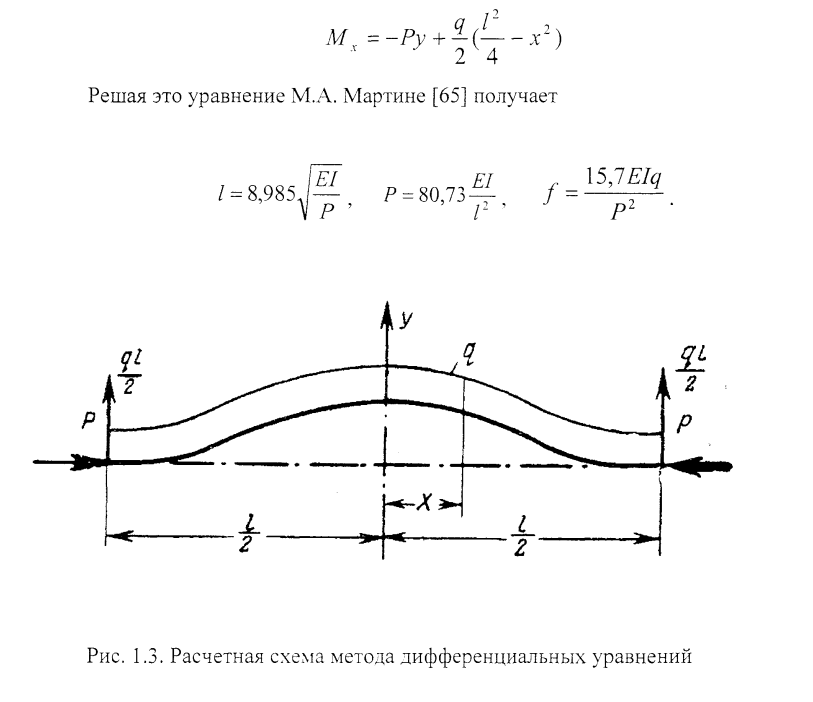
Метод конечных элементов

В 1987 г. J1. ван Хенгструмом была опубликована работа [62] по моделированию устойчивости бесстыкового пути с использованием метода конечных элементов (программа SPAT).

В основу расчетов по программе SPAT положен метод конечных элементов. Выбор такого метода обусловлен нелинейной природой явления, что потребовало в процессе моделирования пошагового приращения температуры рельсовых плетей. Преимуществом метода является возможность исследования при любом очертании пути, включая начальное искривление рельсовой колеи и предельные состояния. Железнодорожный путь в исследуемой модели рассматривается как балка на упругих опорах с постоянной изгибной жесткостью EI и сопротивлением на кручение в узлах скреплений. Сопротивление балласта представлено в виде пружин в поперечном и продольном направлениях. Перемещения в функции температуры происходят в двухмерной горизонтальной плоскости. Каждый из трех упругих элементов имеет билинейную характеристику. Это означает, что вначале сопротивление возрастает пропорционально перемещению, а затем оно становится постоянным, т. е. наступает пластическая фаза. В математической модели допускается упругая реакция пружины при снятии нагрузки, когда достигнута пластическая фаза. Длина элемента балки в модели принята равной расстоянию между осями шпал. Связи обладают тремя степенями свободы: продольное перемещение и, поперечное перемещение v, вращение ф. Графически модель представлена на рис. 1.4.

Уравнения равновесия путевой конструкции, состоящей из элементов балки, дают систему уравнения в виде неизвестных приращений перемещений согласно матричному уравнению вида [S][Av]=[AF], где [S] — матрица тангенциальной жесткости; [Av] — вектор приращения перемещения; [AF] — вектор приращения нагрузки.

Матрица тангенциальной жесткости [S] состоит из трех компонентов:

матрица жесткости элемента балки, [Si], включающая постоянные величины жесткости которые согласно линейной теории выражаются полиномами первой и третьей степеней;

матрица дополнительной жесткости [S2] системы, которая включает коэффициенты, зависящие от вертикальной силы. Эта жесткость отражает геометрические нелинейности в матрице [S];

матрица жесткости балласта и скреплений [S_v], включающая (С_х, С_у, С_ф), которая располагается по главной диагонали матрицы.

Сумма этих жесткостей дает тангенциальную жесткость системы. Условия опирания рельса на шпалы учитываются уменьшением матрицы [S].

После приложения температурной нагрузки и решения статического уравнения равновесия получают вектор перемещения [Av] Затем, задав новое значение суммарного перемещения (v°+Av) и внутренние напряжения, выводят новую тангенциальную жесткость [S]. Обратная подстановка вектора перемещения [Av] дает новый вектор нагрузки [AF*]. Разность между начальным вектором нагрузки [AF] и вектором нагрузки [AF*] является новым вектором нагрузки при новом суммарном перемещении (v°+Av). И так продолжают до тех пор, пока не будет достигнута требуемая точность.

Нагрузка на путь включает две составляющие: температурную и внешнюю нагрузки. Температурная нагрузка обусловлена повышением температуры и возникновением сжимающих продольных усилий в рельсовых плетях. В результате этого может происходить выброс пути в горизонтальной плоскости. Сжимающее усилие Р зависит от разности фактической температуры плети и температуры ее закрепления.

Для проверки работоспособности математической модели также вводили внешние силы, которые прикладывали к связям в поперечном и продольном направлениях. Для этого результаты решения сопоставляли с экспериментальными данными, получаемыми во время измерений на путевой машине Beaver I на одном из участков Нидерландских железных дорог. Нагрузки прикладывали порознь и в сочетании друг с другом. Сопоставление результатов решения по программе SPAT с ранее выполненными исследованиями показало хорошую сходимость.

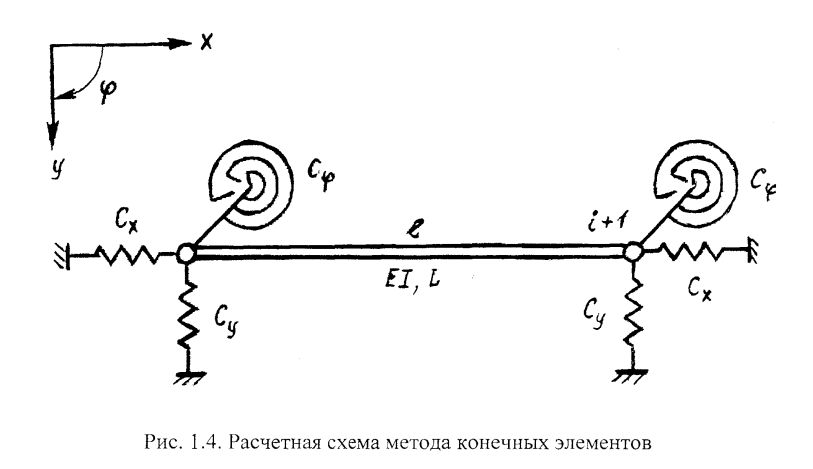
Моделирование отрезка рельсовой плети как балки на опорах

Рассмотрим один из подходов к определению продольных сил в рельсе [50]. Он основан на том факте, что если рельс можно закрепить в двух точках на некотором расстоянии друг от друга и в центре этого отрезка приложить сосредоточенную силу, то конструкция пути ведет себя как балка с закрепленными на опорах концами, а ее прогиб зависит от продольной нагрузки в рельсе и поддается измерению. Очевидно, что сжимающая продольная нагрузка Р будет увеличивать прогиб, а растягивающая нагрузка Т — уменьшать его. Кроме продольной силы, на прогиб влияет жесткость рельса Е1, приложенная нагрузка <3, длина балки Ь (расстояние между закрепленными концами) и способ закрепления концов. Можно сконструировать такое приспособление, которое обеспечит достаточно хорошую воспроизводимость результатов для всех точек контроля и серий измерений.

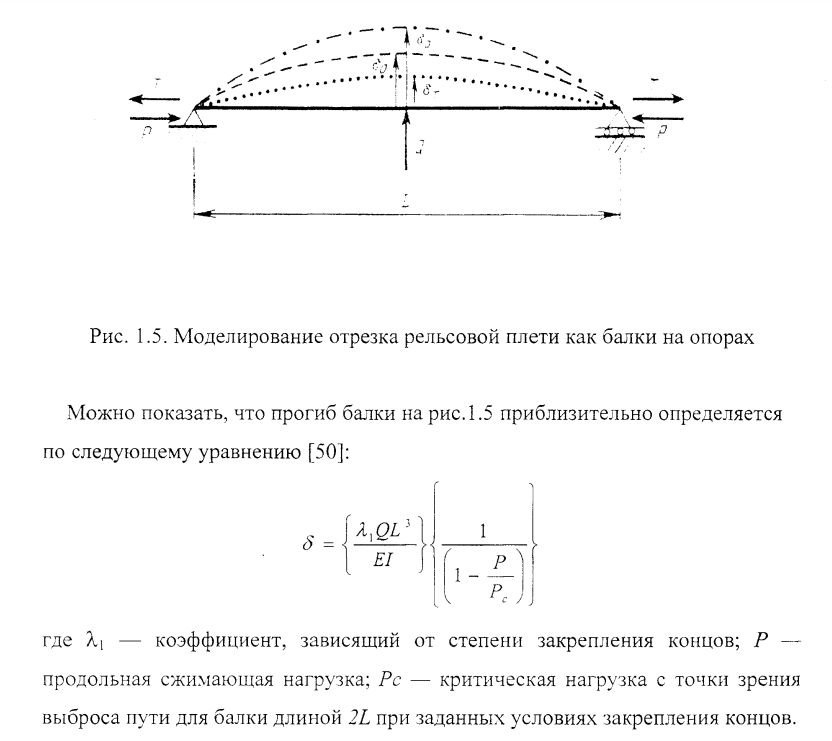
Первый член уравнения представляет прогиб под действием сосредоточенной нагрузки при отсутствии в рельсе какой-либо продольной силы. Второй член — это множитель, учитывающий влияние продольной силы.

Прогиб рельса, закрепленного как балка в двух точках и нагруженного сосредоточенной поперечной или вертикальной силой, может быть использован как мера продольной силы в рельсе.

Экспериментально-теоретический метод

Способы расчета устойчивости бесстыкового пути имеют резные физические основы и допущения, различную полноту учета особенностей бесстыкового пути. Результаты расчета разными способами одной и той же конструкции существенно различаются. Во ВНИИЖТе было предложено непосредственное измерение интервала температур плетей, при которых обеспечивалась устойчивость бесстыкового пути. На специальном стенде [116] собирали рельсошпальную решетку различной конструкции. Рельсовые плети нагревали электрическим током и фиксировали подвижки плети в различных плоскостях. На основе почти 400 опытов получены допускаемые повышения температур рельсовых плетей по сравнению с начальной температурой в момент закрепления для различных конструкций бесстыкового пути.

На основе этих экспериментов и теоретических расчетов во ВНИИЖТе разработаны Технические указания по устройству, укладке, содержанию и ремонту бесстыкового пути [106]. Многолетний опыт эксплуатации бесстыкового пути на сети дорог согласно этим Техническим указаниям, является подтверждением правильности положений экспериментально-теоретического метода [116].

Анализ программных средств определения устойчивости бесстыкового пути

С расширением в начале 70-х годов применения компьютерной техники в научно-технических исследованиях были предприняты и первые попытки математических расчетов на ЭВМ устойчивости бесстыкового пути [23]. Возможным импульсом к этому было интенсивное развитие компьютерной техники и ее применение при исследовании механических процессов, в том числе и в расчетах пути, при моделировании процессов угона пути профессором В. И. Меньшиковой [69].

Д. Игнятич одним из первых при решении проблемы статической устойчивости бесстыкового пути методами математического моделирования включил в модель фактические наблюдаемые случайные по протяжению пути отклонения от проектных норм устройства в содержании бесстыкового пути (фактические случайные формы и размеры неровностей), нелинейные зависимости сил сопротивления от размеров поперечных и продольных перемещений шпал в балластном слое, неравномерности этих сил по протяжению пути, нелинейные и неравномерные по протяжению пути силы и моменты сил сопротивления линейным продольным и угловым перемещениям рельсов в промежуточных рельсовых скреплениях. При этом он использовал численные методы решения дифференциальных уравнений и даже предусматривал использовать в расчетах известные статистические параметры сопротивлений перемещениям шпал в балласте и неровностей пути в плане. В будущем при получении больших компьютерных математических мощностей он предполагал учитывать законы распределения вероятностей в качестве параметров, которыми описываются напряженное состояние и деформации конструкций. В этом исследовании была использована программа М(ЖР11А1Ч, разработанная доктором И. Бановичем.

Математическим моделированием процессов, происходящих в рельсовых плетях бесстыкового пути, занимались С.И. Морозов [74], М.Ф. Вериго [21, 23], Л. ван Хенгструм [62], А. Киш [50].

С.И. Морозов [74] разработал алгоритм и программу позволяющий автоматизировать расчет температурного интервала укладки бесстыкового пути по условиям прочности и устойчивости пути с учетом радиуса кривых и аналитическим определением критической продольной сжимающей силы [75, 76]. Эту программу удобно использовать для анализа различных конструкций температурно-напряженного бесстыкового пути на стадии укладки, но не в процессе эксплуатации.

В 1987 г. на Нидерландских железных дорогах провели исследования поперечной устойчивости бесстыкового пути под воздействием температурных напряжений [62]. В основу расчетов по программе SPAT положен метод конечных элементов. Преимуществом этой программы является возможность исследования при любом очертании пути, включая начальное искривление рельсовой колеи и предельные состояния.

М.Ф. Вериго в работах [21, 23] предлагает теоретико-экспериментальный метод на основе системно-вероятностного подхода к построению динамической модели потери устойчивости бесстыкового пути, реализованный в программах: VIBR, SVTBR3. В исходных данных этой модели учитываются: конкретные формы и размеры неровностей пути в плане; индивидуальные для каждой шпалы на участке силовые характеристики сопротивления их перемещениям в балластной призме поперек пути; индивидуальные характеристики комплектов промежуточных рельсовых скреплений на каждой шпале в виде функций, выражающих зависимость возникших в них моментов сил сопротивления от величин углов поворота (в плане) рельсов в рельсовых скреплениях; индивидуальные реактивные продольные силовые характеристики комплектов промежуточных рельсовых скреплений на продольные перемещения в них рельсовых плетей; эксцентриситеты приложения продольной нагрузки (при различных продольных силах в каждой из рельсовых плетей); кривизна участка пути. Естественно модель с таким количеством исходных данных невозможно использовать для диагностики устойчивости пути в больших объемах. Этот метод применим только для исследовательских целей, и не подходит для диагностики действующего пути.

В связи с резко возросшими возможностями компьютерной техники, как по быстродействию, так и по объемам памяти, появились новые методы оценки V стоичивости [23, 10], например вычислительный комплекс Космос/М фирмы S.R.A.C.

Каждый из упомянутых методов математического моделирования имеет свои недостатки и преимущества. Одни достаточно просты в использовании, но имеют низкую точность, другие более точны, но требуют большого количества исходных данных и поэтому неприемлемы для оценки состояния реального пути. Ряд моделей ориентированы на имитацию собственно процесса выброса пути, в то время как в действующем пути гораздо важнее исследовать процессы, протекающие до выброса, с тем, чтобы его предотвратить.

Расчет сил поперечного сопротивления в идеальном случае должен приводиться в виде эпюры, полученной исходя из измеренной геометрии балластной призмы, ее уплотненности и загрязненности. В настоящее время ведется создание средств диагностики состояния геометрии балластной призмы и земляного полотна, например устройство, описанное в патенте 11112066640. Но пока эти устройства недостаточно отработаны, представляется логичным определять усредненные характеристики балласта на основе данных о сроке службы, грузонапряженности, осевых нагрузках, пропущенном тоннаже и проведенных путевых работах.

Как отмечалось в работе [42], усредненная оценка состояния шпал и скреплений, вполне приемлема для определения устойчивости, т.к. реальное влияние на жесткость путевой решетки, с точки зрения сохранения или нарушения устойчивости, могут оказывать элементы конструкции верхнего строения пути лишь на длине, не меньшей половины длины выброса, что при нормальном содержании пути невозможно. Кроме того, введение в расчетную модель устойчивости пути элементов, моделирующих негодность шпал и скреплений, достаточно сложно, т.к. сами эти “подмодели” почти не подлежат формализации из-за практически бесконечного количества возможных вариантов повреждений шпал и скреплений. Более того, поскольку простые “подмодели” этих элементов в рамках модели устойчивости пути практически невозможны, для реализации сложных потребуется система сбора всех необходимых показателей, т.е. полная дефектоскопия и тензометрия для каждой шпалы, для каждого элемента скрепления, как это предлагается в имитационных моделях Вериго М.Ф. [21]. Но такой подход неприемлем для высокоскоростного автоматизированного средства контроля.

Выводы

Механические и оптические способы контроля продольно-напряженного состояния рельсовой плети достаточно наглядны и просты в реализации, не подвержены влиянию магнитных полей и внутренней структуры рельса, но при этом требуют нанесения дополнительных меток и сложно реализуются в автоматическом режиме.

Ультразвуковые и магнитные методы измерения чрезвычайно чувствительны к структуре рельсового металла, они и применяются, прежде всего, при дефектоскопировании. На изменение напряженного состояния рельса эти приборы безусловно реагируют, причем ультразвуковой тензометр очень хорошо, но при неизменности структуры металла рельса, а в реальном пути это обеспечить невозможно. Этот вывод подтверждается испытаниями ультразвукового тензометра и установки по использованию эффекта Баркгаузена и др. Частично устранить недостатки акустического метода позволяет принцип измерения скорости распространения сигнала вдоль рельса, при этом скорость не зависит от наличия трещин. Но этот принцип сложно реализовать в автоматизированном режиме.

В заключении обзора расчетных методов можно сделать следующие выводы: погрешности приближенного численного решения обусловливаются несколькими причинами. Первая из этих причин может быть та, что выбранная для численного решения математическая модель лишь весьма приближенно описывает физическое явление. Эти погрешности возникают из-за отсутствия:

отчетливой, полной и точной формулировки гипотезы или вообще допущений, служащих основой для составления дифференциальных уравнений;
в некоторых случаях отчетливой и ясной формулировки начальных и граничных условий;
указаний на способы измерений и непосредственные их результаты;
пояснений, какие параметры введены в уравнение, какова точность их определения и сколько их.

Причиной погрешностей таких решений, относящихся уже к методам численных расчетов, может быть использование в них аппроксимации базисными функциями, приводящее к тому, что дифференциальные уравнения и краевые условия удовлетворяются неточно (погрешности дискретизации или аппроксимации).

Столь же важным для практических численных расчетов и исследований устойчивости бесстыкового пути является описание конкретного вида получаемых результатов, т. е. метод должен позволять исследовать и видеть ход происходящих процессов во времени.

До настоящего времени ни одна из описанных математических моделей ни нашла широкого применения в путевом хозяйстве для диагностики напряженного состояния рельсовых плетей бесстыкового пути. Это отчасти связано с тем, что в этих моделях не предусмотрен автоматизированный сбор исходных данных и нет накопления результатов моделирования для анализа изменения параметров бесстыкового пути во времени, например изменение параметров при годовом цикле изменения температуры или с ростом пропущенного тоннажа и др.

Единственным показателем, характеризующим устойчивость пути к выбросу, для текущего содержания бесстьжового пути является исходная температура закрепления рельсовой плети [106]. Однако, как известно, температура закрепления не несет достаточно достоверной информации о напряженном состоянии рельсовой плети, причем ее ценность резко падает во времени. Это происходит, в частности, по следующим причинам: изменение реактивных усилий в скреплениях; релаксационные явления в металле рельса; изменение свойств балластной призмы; образование новых эксплуатационных горизонтальных неровностей; действие тормозных сил и сил угона пути; производство различного вида путеремонтных работ. Все это, в конечном счете, приводит к непредсказуемому перераспределению продольных усилий по длине плети.

Учитывая, что силы сопротивления также претерпевают случайные изменения в пространстве и во времени, диагностика и прогнозирование устойчивости бесстьжового пути представляются как задача, не имеющая пока достаточного информационного обеспечения.

Целью работы является разработка методики и создание надежных диагностических средств для мониторинга бесстыкового пути, позволяющих повысить безопасность движения и сократить эксплуатационные расходы на содержание пути. Для этого должно быть создано специальное измерительное устройство и разработана соответствующая технология диагностики бесстыкового пути.

В работах [40, 50, 7, 41, 42] дан обзор некоторых методов и устройств контроля напряженного состояния рельсовых плетей и сформулирована часть требований которым должны отвечать эти устройства. Их анализ с учетом исследований ВНИИЖТ позволяет сформулировать дополнительные требования к системе контроля напряженного состояния рельсовых плетей. Задача настоящей работы состоит в создании автоматизированной системы контроля, которая обеспечит:

высокую производительность процесса измерения;
определение не среднего продольного напряжения в плети, а распределение этого напряжения по ее длине;
на первом этапе использование существующей системы контроля по “маячным” шпалам. которая позволяет применять как автоматизированный контроль, так и визуальный;
контроль напряженного состояния плетей без нулевой базы измерений и паспортизации;
возможность включения в будущем в автоматизированную систему мониторинга пути для планирования и организации путевых работ.

Список литературы

Александров А. И., Грачев В. Ф. Применение метода конечных элементов в задаче о контакте колеса и рельса // Сб. науч. тр. ДИИТ. Вып. 220/28. Днепропетровск. 1986. С. 118-120.
Альбрехт В. Г., Коган А. Я. Угон железнодорожного пути и борьба с ним // Тр. ВНИИЖТ. М.: Транспорт, 1996. 160 с.
Альбрехт В. Г. Угон бесстыкового пути при проходе тяжеловесных и длинносоставных поездов // Совершенствование конструкции бесстыкового пути: Тр. ВНИИЖТ М.: Транспорт, 1988. с. 44 – 53.
Альбрехт В. Г. О продольных силах, возникающих на поверхности соприкасания подошвы рельса и основания при проходе колес подвижного состава. Труды МИИТ, вып. 80/1, Трансжелдориздат, 1955.
Анализатор напряжений и структуры металлов ИНТРОМАТ / Техническое описание и инструкция по эксплуатации – М.: 1999, 27 с.
Ангелейко В. П., Зоткин Н. М. О целесообразности применения теории ползучести к расчету устойчивости бесстыкового пути // Вестник ВНИИЖТ. 1980. № 2. с. 46- 47.
Балух X. Диагностика верхнего строения пути / Пер. с польского И. В. Шварца / Под ред. М. Ф. Вериго. М.: Транспорт, 1981. 415 с.
Бартлет Д.. Устойчивость бесстыкового пути /Перевод ЦНТБ МПС П-8737. 59 с.
Бесстыковой путь / Под ред. В. Г. Альбрехта и Е. М. Бромберга. М.: Транспорт, 1982. 206 с.
Бесстыковой путь / В.Г. Альбрехт, Н.П. Виногоров, Н.Б. Зверев и др.; Под ред. В. Г. Альбрехта, А.Я. Когана. – М.: Транспорт, 2000. 408 с.
Бирманн Ф. Опыт применения бесстыкового пути на Федеральных германских железных дорогах // Бесстыковой железнодорожный путь Перевод с нем. В. Д. Никифоровского и А. М. Шкитиной. М.: Трансжелдориздат, 1959. С. 140 – 172.
Боченков М. С. Зазоры при изломе рельсовой нити // Тр. ВНИИЖТ. Вып. 244. М.: Трансжелдориздат, 1962. С. 164- 172.
Боченков М.С. Исследование угона железнодорожного пути при современных конструкциях подвижного состава и верхнего строения пути. Труды НИИЖТа; вып. 74, Новосибирск, 1969 г. С. 48-88.
Бойл Дж., Спенс Дж. Анализ напряжений в конструкции при ползучести. М.: Мир, 1986.360 с.
Бромберг Е. М. Перспективы и проблемы развития бесстыкового пути на железных дорогах СССР // Тр. ВНИИЖТ. Вып. 244. М.: Трансжелдориздат, 1962. С. 5-18.
Бромберг Е. М. Устойчивость бесстыкового пути. М.: Транспорт, 1964. 66 с.
Бромберг Е. М., Зверев Н. Б. Бесстыковой путь в кривых. М.: Транспорт, 1968. С. 3-31.
Бромберг Е. М. Устойчивость бесстыкового пути под поездами //Совер-шенствование конструкции и эксплуатации бесстыкового пути: Тр. ВНИИЖТ. М.: Транспорт, 1988. С. 13-20.
Бромберг Е. М. Устойчивость бесстыкового пути при совместном действии поездной и температурной нагрузок // Повышение эффективности бесстыкового пути: ВНИИЖТ. М.: Транспорт, 1983. С. 77 – 85.
Бромберг Е. М., Хвостик Г. С. Сопротивление сдвигу ненагруженных шпал в балласте//Вестник ВНИИЖТ. 1983. № 2. С. 49 – 51.
Вериго М. Ф. Динамические модели устойчивости бесстыкового пути // Железные дороги мира. 1994. № 10. С. 3 – 9.
Вериго М. Ф. Создание нормативной базы для повышения устойчивости
бесстыкового пути и расширения его применения // Железные дороги мира, N6, 1996. С.41-49
Вериго М.Ф. Новые методы в установлении норм устройства и содержания бесстыкового пути / ВНИИЖТ.- М.: Интекст, 2000. 184 с.
Вериго М. Ф., Коган А. Я. Взаимодействие пути и подвижного состава. М.: Транспорт, 1986. 559 с.
Вериго М.Ф. Создание нормативной базы для повышения устойчивости бесстыкового пути и расширения сфер его применения // Железные дороги мира. 1996. № 6. С. 41—49.