Цикл статей:
Глава 1 – Напряженное состояние рельсовой плети и методы его определенияГлава 2 – Исследование факторов, влияющих на формирование продольных сил в плети
Глава 3 – Метод определения напряженного состояния плети
Глава 4 – Автоматизированная система контроля напряженного состояния плетей бесстыкового пути
Взаимосвязь продольных и поперечных подвижек плети
Один из возможных вариантов диагностики М.Ф. Вериго предложил способ определения устойчивости бесстыкового пути, нашедший отраженное в патенте БШ 2038441 С1. Формула изобретения зафиксирована в следующем виде: «Способ определения состояния рельсо-шпальной решетки эксплуатируемого железнодорожного пути, преимущественно ее продольно-поперечной устойчивости под действием в ней продольных сжимающих сил, заключающийся в том, что путеизмерительными средствами непрерывно измеряют кривизну рельсовых плетей в плоскости пути, отличающийся тем, что, измеряя кривизну рельсовых плетей, периодически измеряют температуру этих же плетей при помощи бесконтактных температурных датчиков, определяют средние значения продольных сжимающих каждую рельсовую плеть сил по выражению

и сравнивают значения последних сил Н с допускаемыми их значениями для данного участка пути». Измерение кривизны рельсовых плетей предусмотрено производить инерционным способом по авторскому свидетельству СССР № 312914 от 2 июня 1971 г., авторы: М. Ф. Вериго, А. Я. Коган, Ю. С. Ромен.
Входным параметром в этой системе являются значения температур закрепления каждой рельсовой плети Т3, а на выходе из компьютера планировалось получать кривые соотношения сил Н/Ндоп, где Ндоп —допускаемое значение сдвигающей рельсошпальную решетку силы.
В этом авторском свидетельстве не говорится о том, что считать допускаемым значением Ндоп. Кроме того, при диагностике плетей длиной несколько тысяч метров усреднение значение температуры по длине может внести существенную погрешность. Представляется целесообразным определять не средние значения параметров по длине плети, а использовать их в виде эпюры. Это крайне необходимо при диагностике плетей длиной до перегона, когда параметры бесстыкового пути имеют значительную неравномерность распределения по длине.
Автором настоящей работы в соавторстве с Н.П. Виногоровым [109] предложено решение, отраженное в патенте 1Ш 2174082 С1. Это решение предполагает определять продольно-напряженное состояние рельсовых плетей исходя из их продольных подвижек.
Предлагается продольные и поперечные составляющие напряженного состояния бесстыкового пути рассматривать совместно. В связи с этим предложена следующая схема (рис. 3.1 один из возможных вариантов), позволяющая определять участки бесстыкового пути, на которых наиболее вероятен выброс. В этой схеме оба предложенных решения рассматриваются параллельно, а на заключительном этапе наиболее опасные участки определяются по двум критериям: Н/Нкр и М/Мкр, приоритетным считать тот критерий, чье значение больше. Недостаток этой схемы в том, что вклад продольных и поперечных подвижек плети рассматривается отдельно и сравнивается только в конце.
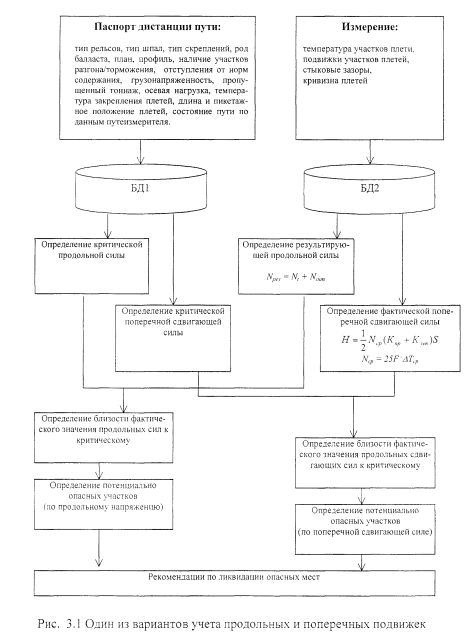
Оценка безопасности эксплуатации бесстыкового пути по условию его выброса с учетом фактического состояния
Устойчивость бесстыкового пути по условиям выброса определяется его продольно-напряженным состоянием и неровностями в плане [54]. Исходя из этого, предлагается способ оценки безопасности эксплуатации бесстыкового пути с учетом его продольно-напряженного состояния и фактического геометрического положения в плане.
Определение результирующего значения продольного напряжения для конкретного участка плети


Изложенный метод определения продольно-напряженного состояния плетей реализован с участием автора в виде автоматизированной системы контроля смонтированной на путеизмерительном вагоне ЦНИИ-4М. Бесконтактный датчик температуры представляет собой инфракрасный пирометр М67 производства фирмы MIKRON. Устройство определения границ плети реализовано на базе датчиков величины стыковых зазоров, разработанных и изготовленных ПИК ПРОГРЕСС. Устройство определения подвижек плети разработано во ВНИИЖТ с участием автора совместно с ПИК ПРОГРЕСС. Полевые испытания макетного образца этого устройства проведены в ноябре 2000 г. С учетом замечаний по результатам этих испытаний разработан и изготовлен опытный образец указанного устройства, который успешно прошел испытания в 2001 г. Этот опытный образец позволяет определять смещения рельсовой плети и отдельных ее участков в автоматизированном режиме без учета скорости движения считывающего устройства посредством отслеживания изменения положения меток на рельсовой плети относительно маячных шпал с достаточной точностью и помехозащищенностью [109].
Взаимосвязь критического значения продольного напряжения в плети с амплитудой и длиной неровности
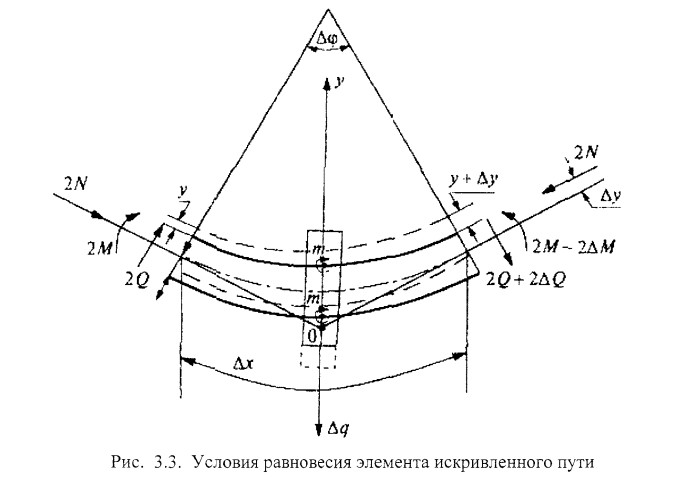
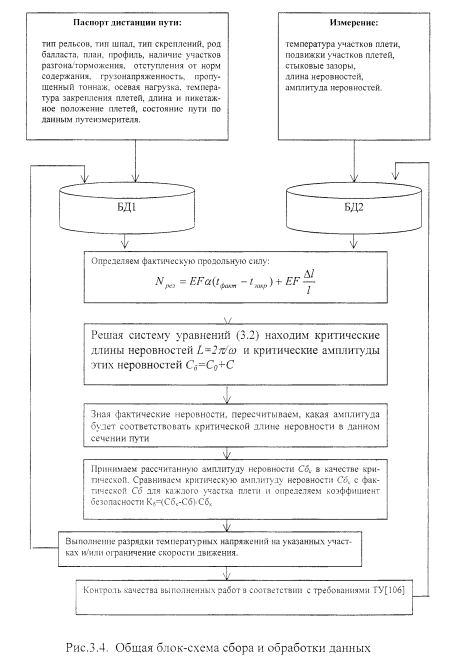
Исходя из того, что продольные и поперечные подвижки бесстыкового пути не должны рассматриваться в отрыве друг от друга, автором предлагается следующая методика рис. 3.4, позволяющая определять участки бесстыкового пути, на которых наиболее вероятен выброс. Эта методика диагностики продольно-напряженного состояния бесстыкового пути позволяет учесть как продольные подвижки участков пути, вызванные температурной деформацией и угоном, так и поперечные подвижки (горизонтальные неровности), которые так же могут быть вызваны изменением температуры и воздействием поездной нагрузки. Продольные подвижки характеризуют степень затяжки гаек клеммных болтов и сопротивление шпал перемещению вдоль пути (в частности заполнение шпальных ящиков балластом). Поперечные подвижки характеризуют жесткость рельсошпальной решетки в горизонтальной плоскости и сопротивление шпал перемещению поперек пути (в частности ширину плеча балластной призмы). Кроме того, предлагаемая методика и соответствующие программно- аппаратные средства позволяют не усреднять продольные напряжения в плети, а получать их в виде эпюры по длине плети. Это особенно актуально в последнее время, когда плети достигают длины блок-участка, перегона. Для расчета критического значения продольного напряжения в плети за основу взята методика, изложенная в [54]. Эта методика расчета учитывает взаимосвязь критической температурной силы в рельсе с размерами неблагоприятной неровности в кривых (в частном случае в прямой). Рассматривается равновесие элемента пути Ах размером, равным расстоянию между соседними шпалами (рис. 3.3).


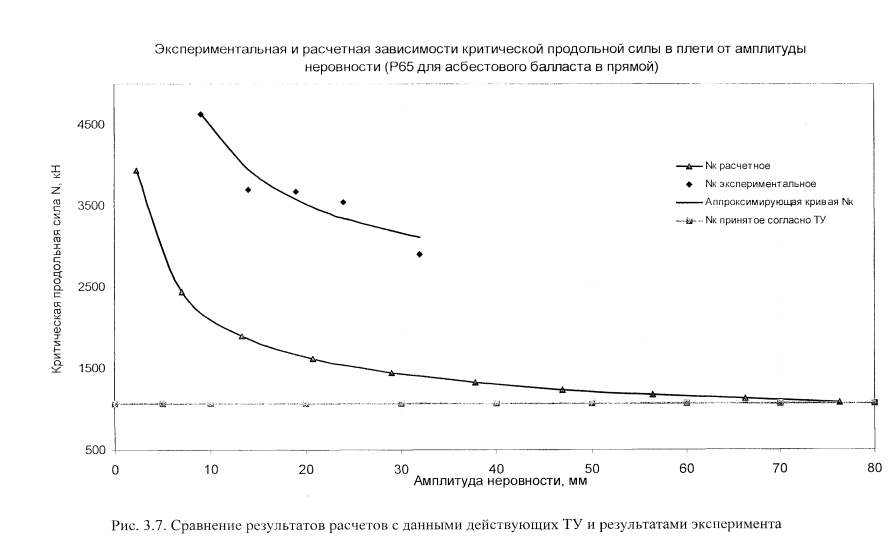
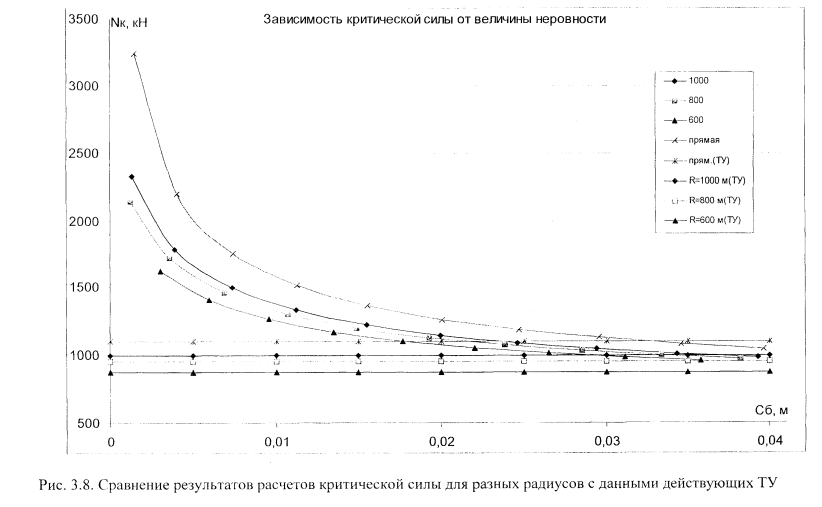
Для решения этой системы уравнений методом последовательного приближения автором настоящей работы составлена программа на языке \%иа1Ва- бхс. Достоверность работы программы подтверждена тем, что ее результаты идентичны результатам, которые получил А .Я. Коган [55]. После чего в программу вводились данные для различных участков пути и значения критической продольной силы сравнивались со значениями, приведенными в технических указаниях на бесстыковой путь [106] и с экспериментальными данными [9. 47]. Результаты этого сравнения приведены на рис. 3.7 и рис. 3.8. На рис. 3.8 видно, что полученные расчетные значения критической продольной силы при амплитудах неровности более 2 см близки к значениям, полученным согласно ТУ [106]. При амплитудах неровности менее 2 см наблюдается значительное увеличение запаса устойчивости. На рис. 3.7 представлены зависимости критической продольной силы от амплитуды неровности, полученные экспериментально Е.М. Бромбергом, рассчитанные по формуле (3.2) и полученные согласно ТУ [106]. Отличие расчетных данных от экспериментальных в сторону увеличения запаса устойчивости объясняется тем. что расчет выполнен для наихудшей формы начальной неровности, в то время как выброс пути происходит не при самой плохой ее форме. Наихудшей формой является периодическая неровность с критической амплитудой и неограниченным числом периодов.

Из таблицы 3.1 видно, что коэффициент запаса К32 меньше чем К31, особенно при амплитудах неровности менее 2 см, но при этом он все равно не менее двух. При этом коэффициент К32 практически не зависит от амплитуды неровности, так как форма графика критической продольной силы от амплитуды неровности для экспериментальной и расчетной зависимости одинаковы.
Для разработанной программы автором предполагается использовать данные о положении пути в плане по результатам прохода путеизмерительного вагона ЦНИИ-4.
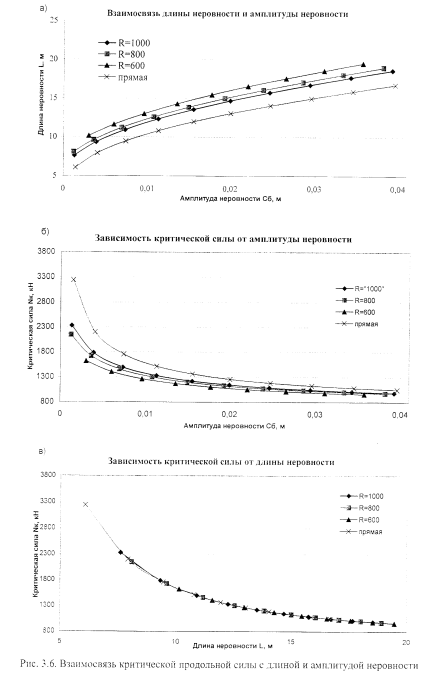
В [55] построена зависимость критической силы и длины неровности от амплитуды неровности. При этом на зависимость Ь = Ь(С6) влияет радиус кривой, а на зависимость М~ N(1) радиус кривой не влияет (рис. 3.6. в). Эта особенность дает возможность не учитывать радиус кривой при определении зависимости критической силы от длины неровности (и наоборот, длины неровности от силы).
Для системы уравнений (3.2) к расчетам предлагаются коэффициенты В и b в аппроксимирующей функции сопротивления шпалы поперечным перемещениям в зависимости только от типа балласта. Вместе с тем имеются исследования ВНИИЖТ по установлению зависимости сопротивления шпал поперечному сдвигу, например от пропущенного тоннажа. Автор настоящей работы считает что, аппроксимировав эти зависимости той же функцией арктангенса, но с различными коэффициентами В и Ъ можно перейти к зависимости этих коэффициентов от пропущенного тоннажа. После чего, эти зависимости в свою очередь можно описать некоторой функцией, которая будет использоваться на входе программы определения коэффициента безопасности. Таким образом, на входе программы будут задаваться на сами коэффициенты, а пропущенный тоннаж, что повысит адекватность модели реальному состоянию пути. Аналогичным образом можно поступить относительно зависимости сопротивления сдвигу шпалы от профиля балластной призмы и от заполнения шпальных ящиков балластом. Это тем более актуально, что в последнее время активно ведутся работы по созданию средств диагностики профиля балластной призмы, например фирмой ПИК ПРОГРЕСС, путем оцифровки видеоизображения с последующим программным анализом.
Таким образом, открывается возможность создания высокопроизводительной диагностической системы на вагоне ЦНИИ-4МД, которая будет выявлять на пути наиболее опасные места с точки зрения выброса.





Обоснование предлагаемой методики определения продольных напряжений в плетях
В настоящее время с достаточной точностью и высокой производительностью можно контролировать ряд параметров бесстыкового пути, влияющих на его напряженное состояние. С учетом требований к системе контроля, изложенных в главе 1, эти параметры целесообразно использовать для определения напряженного состояния рельсовых плетей, для этого предполагается оборудовать путеизмерительный вагон дополнительными средствами диагностики
Основные положения
- В современных условиях, когда длина плети достигает нескольких километров, температура ее различных участков может колебаться в значительных пределах, что может вызывать достаточно большую разницу в напряжении различных участков плети. Следовательно, нельзя усреднять температуру плети по ее длине. Поэтому температура измеряется по всей длине плети и усредняется по длине участков, на которых измеряем подвижки. Таким образом, получаем распределение температуры по длине плети.


Выбор расстояния между реперами (контрольными точками)

При длине угоняемого участка до 100 м максимальные остаточные напряжения не превышают 10-16 МПа, что соответствует изменению нейтральной температуры на 5-6°С. При погрешности измерения смещений ±2 мм погрешность определения дополнительных напряжений от сил угона не превышает 1015 МПа, что можно считать вполне допустимым
Выводы
Предлагаемая методика определения продольно-напряженного состояния рельсовых плетей бесстыкового пути позволяет:
- определить зависимости между продольным напряжением, амплитудой и длиной неровности бесстыкового пути;
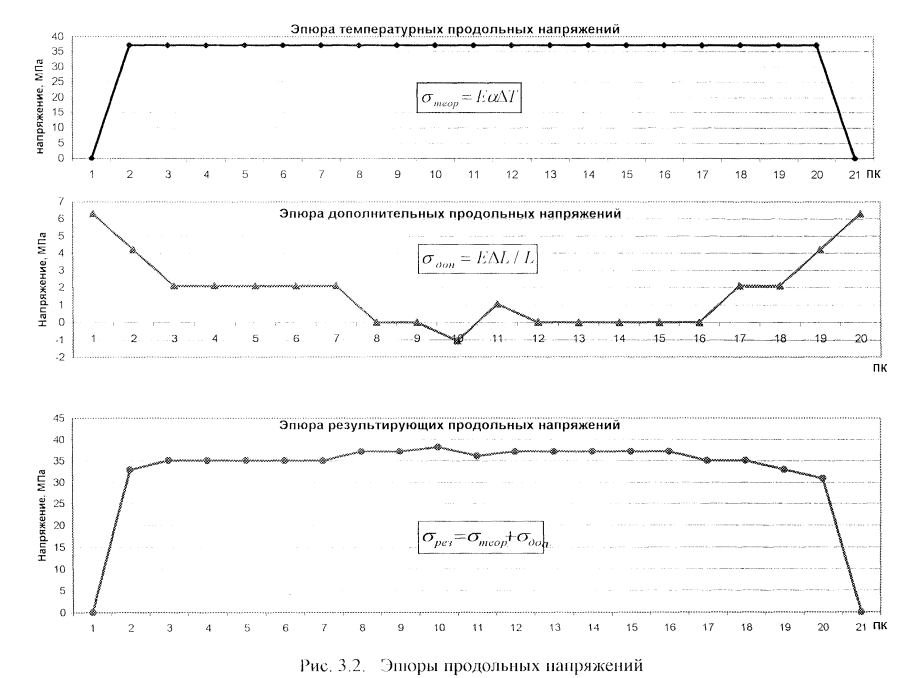
- определить результирующее продольное напряжение на каждом участке плети как сумму теоретического продольного напряжения, рассчитанного по разности фактической и нейтральной температуры плети и дополнительного продольного напряжения вызванного неравномерными подвижками участков плети;
- получить распределение продольного напряжения в виде эпюры по длине плети, а не среднее значение;
- определить устойчивость бесстыкового пути против выброса не только по отношению критического продольного напряжения к фактическому, но и по отношению критической амплитуды неровности для результирующего продольного напряжения к фактической амплитуде неровности.
Предложенная методика позволяет оценивать безопасность эксплуатации бесстыкового пути с учетом его реального продольно-напряженного состояния и фактического геометрического положения в плане. Кроме того, она дает возможность создать автоматизированную систему контроля напряженного состояния рельсовых плетей бесстыкового пути устанавливаемую на путеизмерительном вагоне.
Список литературы
- Коган А.Я. Динамика пути и его взаимодействие с подвижным составом. — М.: Транспорт, 1997. 326 с.
- Коган А.Я., Полещук И.В. Взаимосвязь критической температурной силы в рельсе с размерами неблагоприятной неровности // Вестник ВНИИЖТ, №7, 2000. С.3-7
- Контроль за продольными силами в рельсовых плетях. Виногоров Н.П., Зверев Н.Б. Отчет о НИР ВНИИЖТ МПС. Архив ВНИИЖТ № 1-78, 1985. 51 с.
- Крейнис 3. JI. Метод расчета температурной амплитуды рельсовых плетей // Ученые записки ВЗИИТ. Вып. 13. М.: Изд-во ВЗИИТ, 1964. С. 45 — 58.
- Крейнис 3. JI. Точно определять температуру рельсов // Путь и путевое хозяйство. 1964. №6. С. 15-16.
- Кривободров А. А. Устойчивость железнодорожного пути при температурном воздействии на рельсы // Тр. ЛИИЖТ. Вып. 144, 1952. С. 120¬154.
- Клинов С. И. Повышение устойчивости и расширение сфер применения бес-стыкового пути: Докторская диссертация. М.: МИИТ, 1989. 5 10 с.
- Клинов С. И. Оптимизация температурного режима бесстыкового пути // Железные дороги мира. 1992. № 12. С. 2 — 8.
- Ленгструм Л. В. Анализ устойчивости по методу конечных элементов // Железные дороги мира, №6, 1989, С.64-65
- Лягценко В.Н. 0 продольных динамических горизонтальных силах, возникающих при взаимодействии колеса с рельсом. Труды ХИИТа, вып.81, «Транспорт», 1966. С. 19-28.
- Лысюк B.C., Барабошин В.Ф. Причины интенсивной осадки пути при железобетонных шпалах / Труды ЦНИИ МПС. Вып. 370. Влияние жесткости и неровностей пути на деформации, вибрации и силы взаимодействия его элементов. 1969. С. 7-44.
- Мартине А. Выпучивание бесстыкового пути в балласте и рельсы большой длины /У Rev. Jen. de Chemins de Fer. 1936 №4. P. 212-231.
- Майер Г. Упрощенный метод теоретического исследования выброса бесстыкового пути / Перевод ЦНТБ МПС, П-8264. 65 с.
- Маркарьян М. А., Зверев Н. Б. Сопротивление бесстыкового пути перемещениям //Тр. ВНИИЖТ. Вып. 244. М.: Трансжелдориздат, 1962. С. 19 -45.
- Межелайтис В.А. Контроль температурного режима плетей. — Путь и путевое хозяйство, 1983, №11, С. 28-29.
- Меньшикова В. И. Динамические продольные силы и перемещения рельсов железнодорожного пути (угон рельсов) // Тр. ВНИИЖТ. Вып. 466. М.: Транспорт. 1972. С. 83- 189.
- Метод измерения напряжений в плетях бесстыкового пути, основанный на использовании эффекта анизотропии магнитной проницаемости // Путь и путевое хозяйство, 1974, №7, С.68-71.
- Мищенко К. Н. Бесстыковой рельсовый путь. М.: Трансжелдориздат, 1950. 62 с.
- Мусихин С.А., Новиков В.Ф., Боренко В.Н. Об использовании коэрцитивной силы в качестве индикаторного параметра при неразру- шающем контроле механических напряжений // Дефектоскопия, 1987, N3, С.57-60.
- Морозов С. И. Устойчивость температурно-напряженного железнодорожного пути: Автореферат докторской диссертации. М.: ВНИИЖТ, 1982. 35 с.
- Морозов С.И. Применение ЭВМ для определения температурного диапазона укладки рельсовых плетей. //Вестник ВНИИЖТ, №3, 1997. С. 12-15
- Морозов С.И. Аналитическое определение критической силы для температурно-напряженного железнодорожного пути в прямых участках. // Лесной журнал. 1982, №5, С. 46-54.
- Морозов С.И. Критическая сила для участков пути узкоколейных железных дорог на закруглениях в плане // Лесной журнал. 1982. №6. С. 60-68.
- Морозов С.И. О диагностике устойчивости бесстыкового пути. // Вестник
ВНИИЖТ, №6. 1986, С.51-54 - Мишин В.В., Певзнер В.О. Управление техническим состоянием пути. // Железнодорожный транспорт, №12, 1999, С.66-69
- Надежность железнодорожного пути / B.C. Лысюк, В.Б. Каменский, Л.В. Башкатова; Под ред. B.C. Лысюка. -М.: Транспорт, 2001. 286 с.
- Нгуен Ван Туен. Определение допускаемой температурной продольной силы на прямых участках бесстыкового пути (на основе теории случайных функций): Автореферат кандидатской диссертации. М.: МИИТ, 1970. 18с.
- Немешди-Немшек И. О выборе бесстыкового пути / Перевод ЦНТБ МПС П- 8093. 42 с.
- Немчек Э. Расчет горизонтальной устойчивости бесстыкового пути / Перевод ЦНТБ МПС П-7850. 58 с.
- Нумато М. Сопротивление сварных длинных рельсов продольному изгибу/ Перевод ЦНТБ МПС П-8465. 29 с.
- Новакович В. И. Бесстыковой железнодорожный путь с рельсовыми плетями неограниченной длины. Львов: Вигца школа, 1984. 99 с.
- Нефедов А. А., Ершов В. В., Шабанов JI. А. Температурные эквиваленты не-исправностей бесстыкового пути // Путь и путевое хозяйство. 1995. № U.C. 2-3.