Цикл статей:
Глава 1 – Вибродиагностика подшипников грузовых вагонов Глава 2 – Математическая модель вибраций колесной пары и буксового узла при наличии дефектов
Глава 3 – Функционирование математической модели на пвм
Глава 4 – Компьютерная диагностика неисправностей подшипников
Краткое описание программы для ПВМ
На основе изложенного автором разработана программа для ПВМ, которая осуществляет численный анализ математической модели, представленной векторным дифференциальным уравнением (2.21). Эта программа состоит из нескольких вычислительных и функциональных блоков, которые взаимодействуют под управлением главной программы.
К функциональным и вычислительным блокам, составляющим программу, относятся:
- ввод исходных данных;
- вычисление элементов матриц [ш], [С] и [В] в дифференциальных , уравнениях (2.21);
- формирование возмущений, вызванных неисправностями подшипников;
- формирование векторов Г и дифференциальных уравнениях
- вычисление собственных частот и форм колебаний и определение верхней границы шага интегрирования;
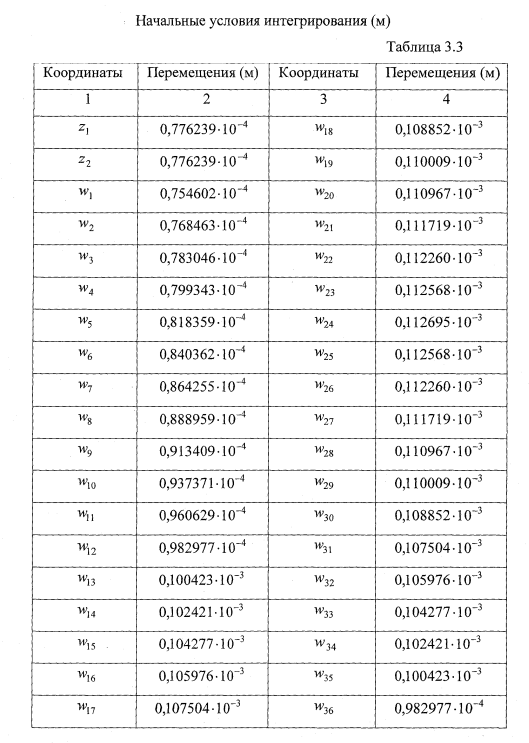
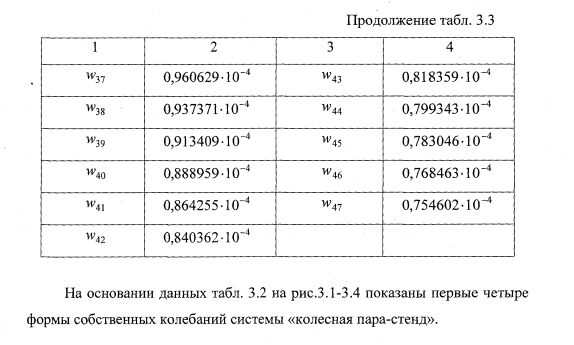
- вычисление начальных условий интегрирования;
- численное интегрирование дифференциальных уравнений (2.21);
- анализ расчетной информации;
- графическое и файловое представление результатов на экране и принтере.
Главная программа осуществляет сборку этих блоков в единый вычислительный комплекс, который дает анализ динамического состояния колесной пары с буксами при ее вращении на стенде. В качестве анализируемых параметров расчета приняты ускорения корпусов букс.
При проведении расчетов на ПВМ формируется файл текущих ускорений корпусов букс, затем формируется графический файл и выбираются максимальные значения ускорений, полученные на заданной временной реализации.
В качестве исходных данных вводятся: геометрические размеры оси и стенда, модуль упругости и плотность материала оси, контактная жесткость роликов и колец подшипников, жесткость основания стенда, коэффициенты внутреннего сопротивления, частота вращения колесной пары на стенде и сопротивление вращению, максимальное время расчетов, шаг интегрирования по времени, шаг дискретизации дифференциальных уравнений и другие величины, необходимые для организации вычислительного процесса.
Так как расчетные упругие перемещения колесной пары с буксами на стенде малы (составляют десятые и сотые доли миллиметра), то программа вычислений была разработана для чисел двойной длины, что соответствует девяти десятичным разрядам мантиссы, при этом точность представления чисел составляла 0,1 • 10±9.
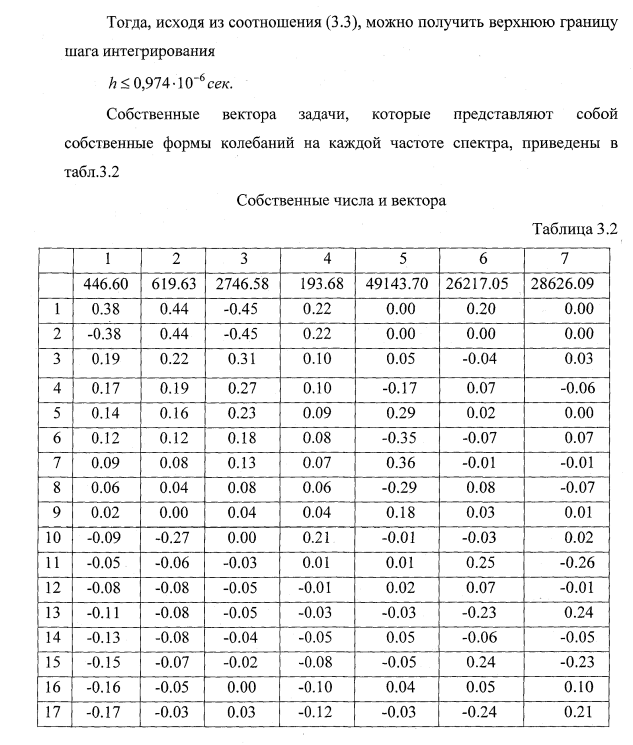
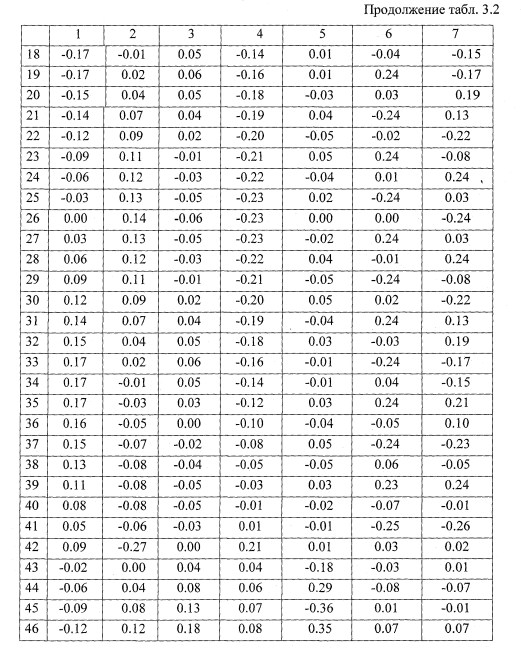
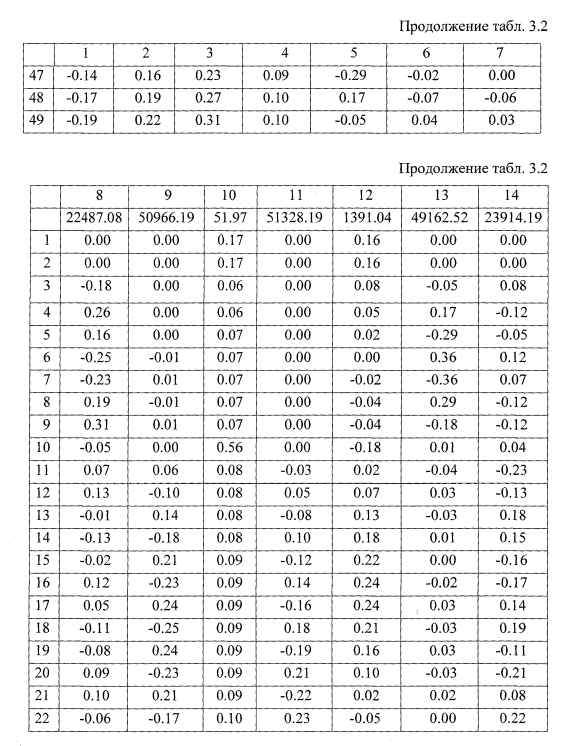
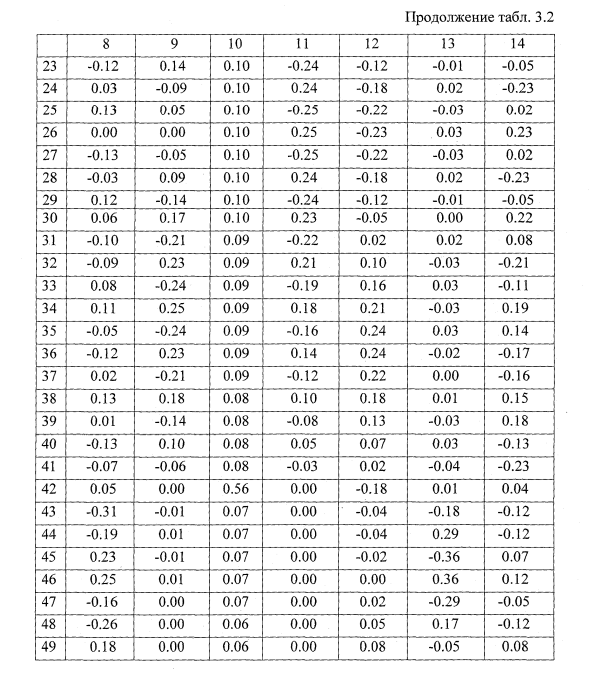
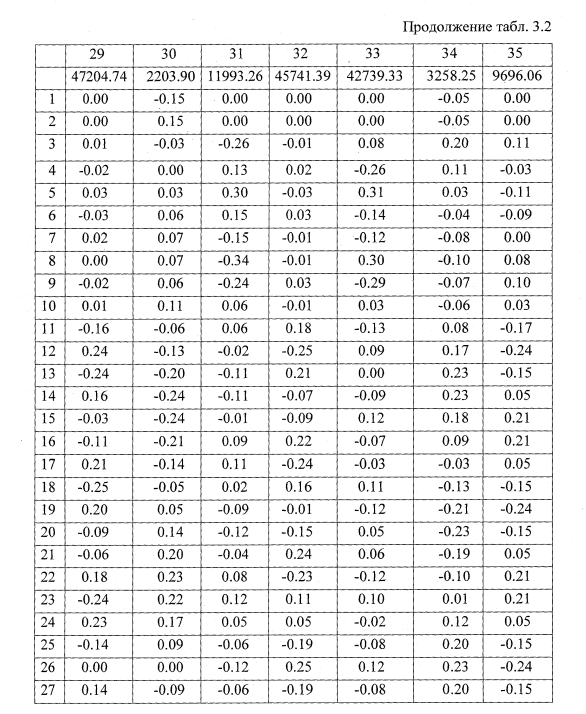
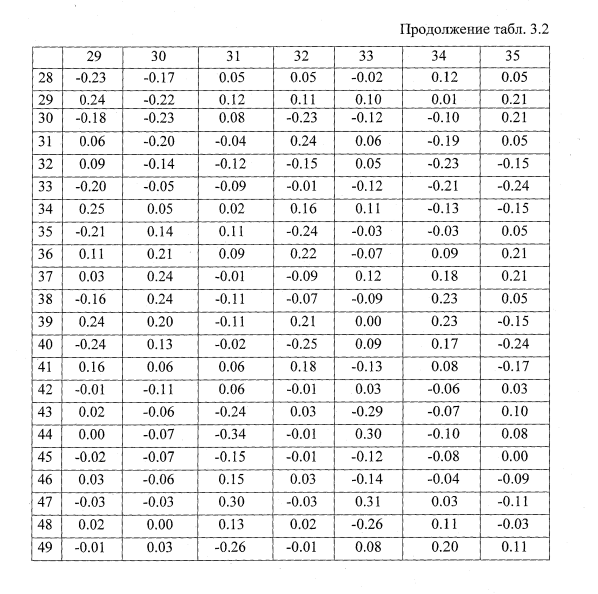
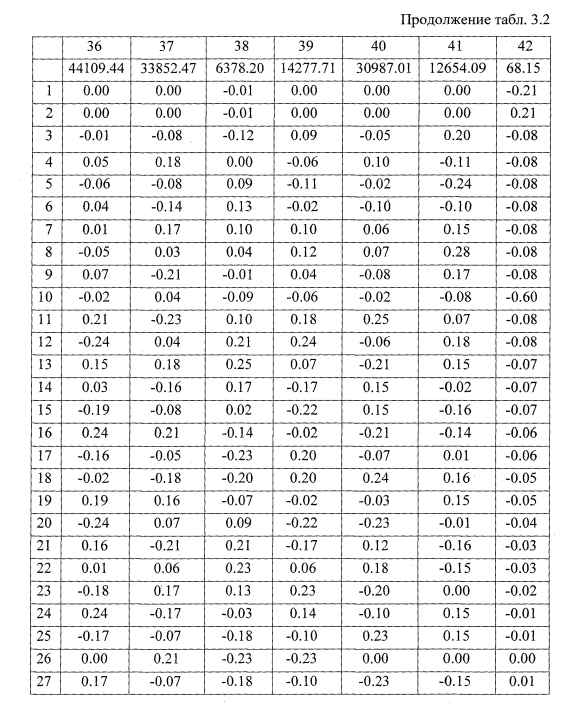
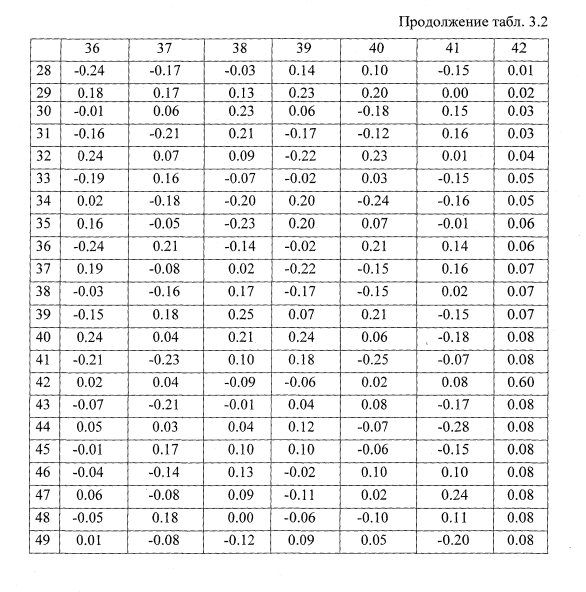
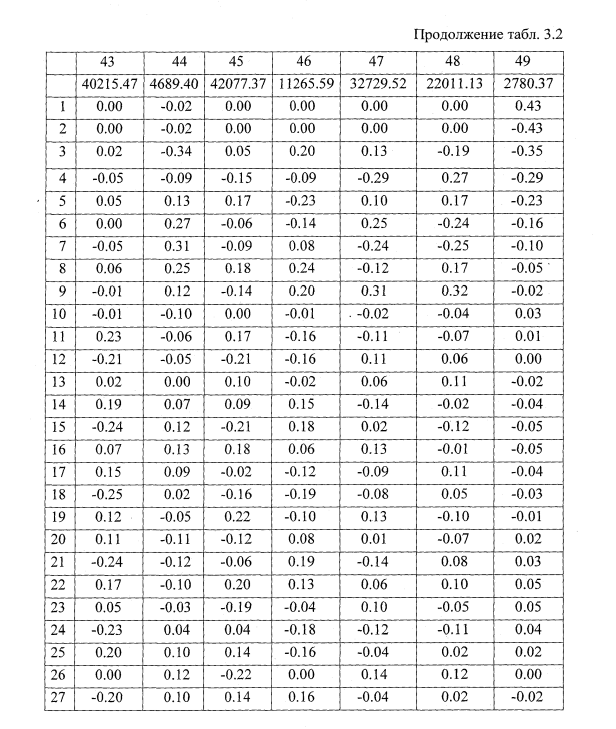
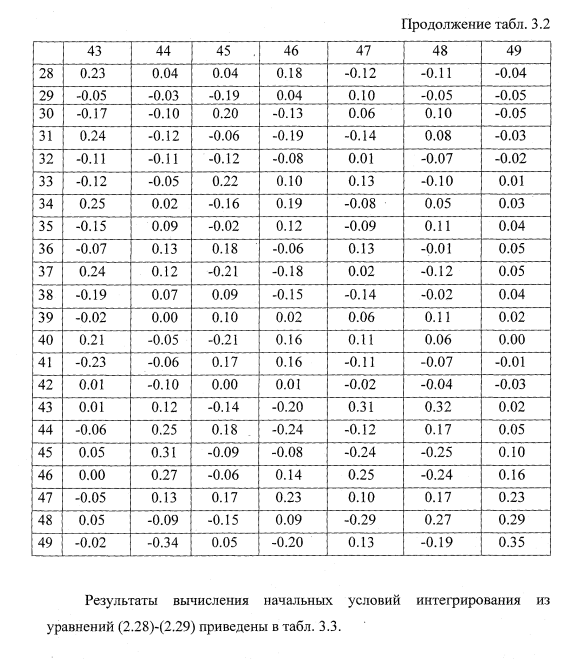
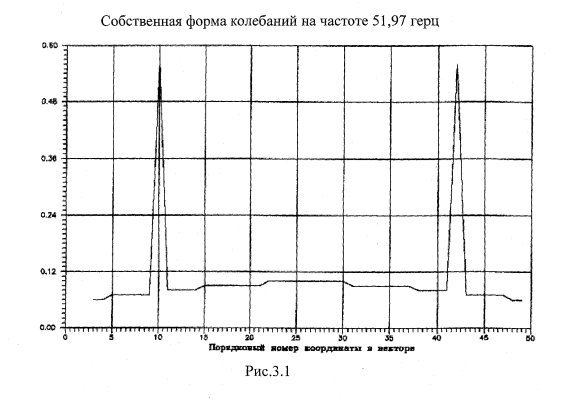
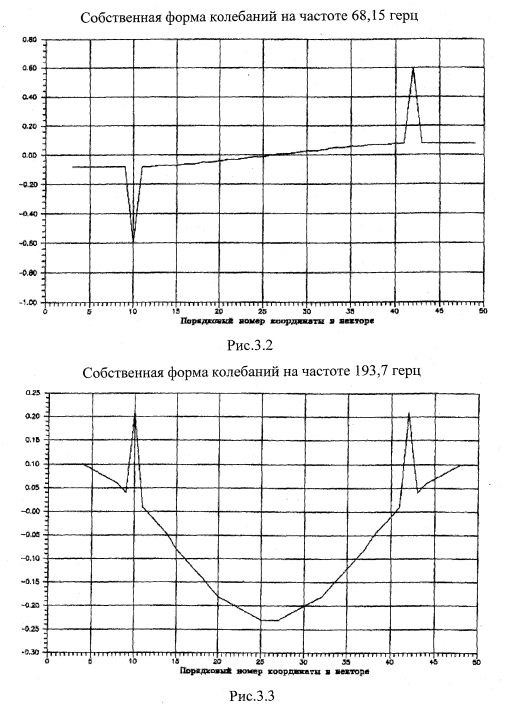
Собственные числа и вектора
Применительно к поставленной задаче (2.41), собственные числа и вектора представляют собой собственные частоты и формы упругих колебаний колесной пары на стенде. Решение поставленной задачи проводилось по подпрограмме, реализующей нахождение собственных значений по методу вращения векторов, предложенному Якоби [50].

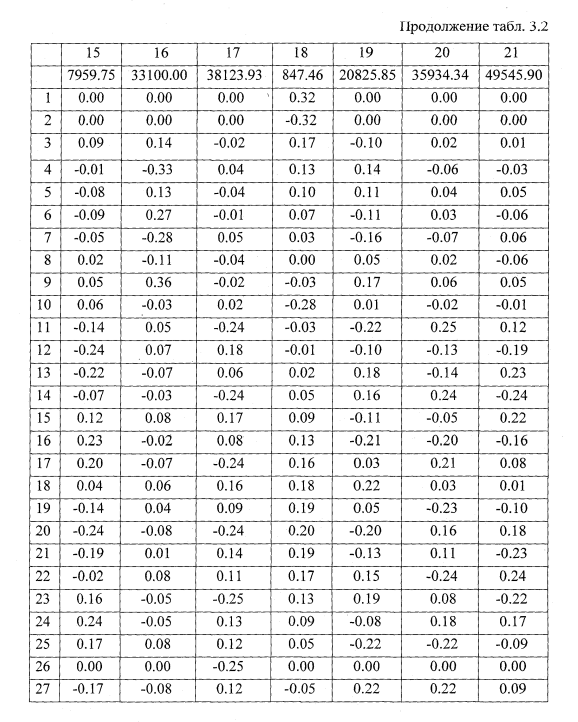
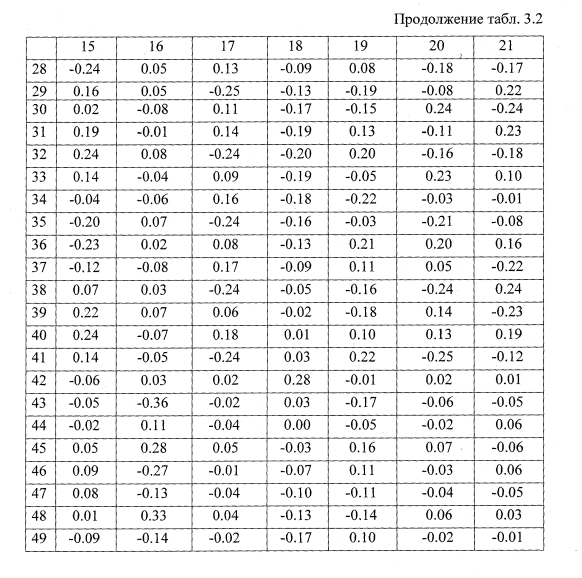
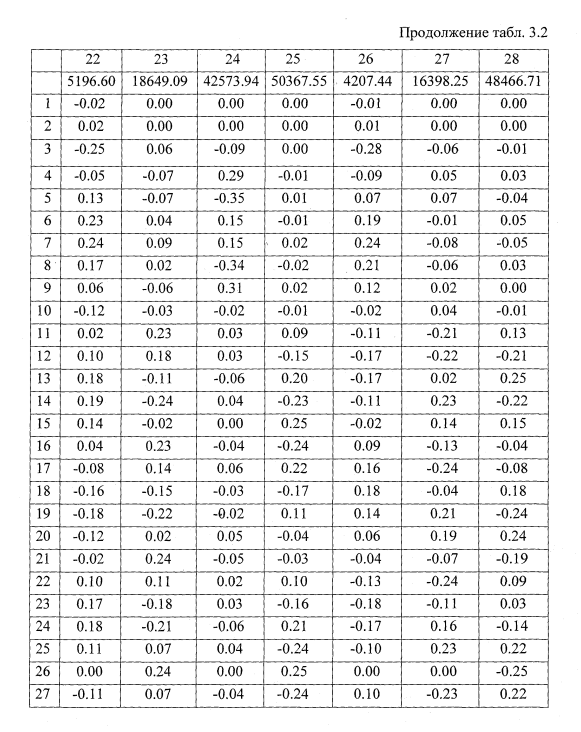
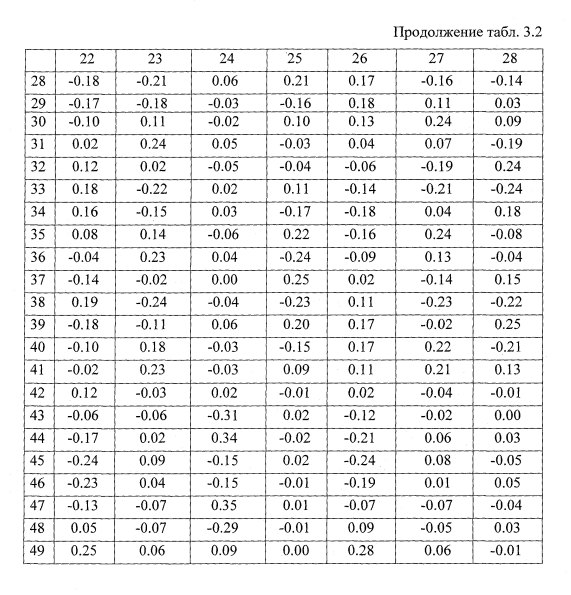
Функционирование программы интегрирования
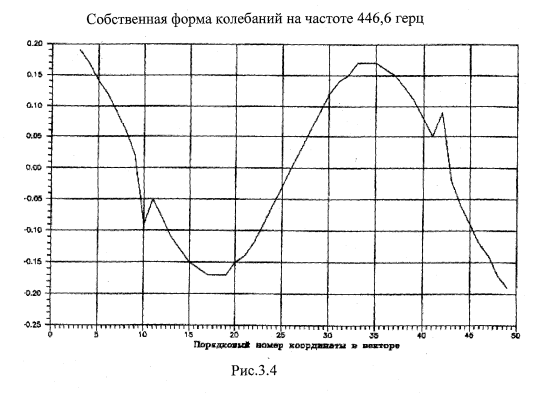
Для иллюстрации функционирования программы интегрирования дифференциальных уравнений (2.21) проведены расчеты вибраций изучаемой системы, когда два ролика переднего и заднего подшипников одной буксы имеют вдоль образующей трещины.
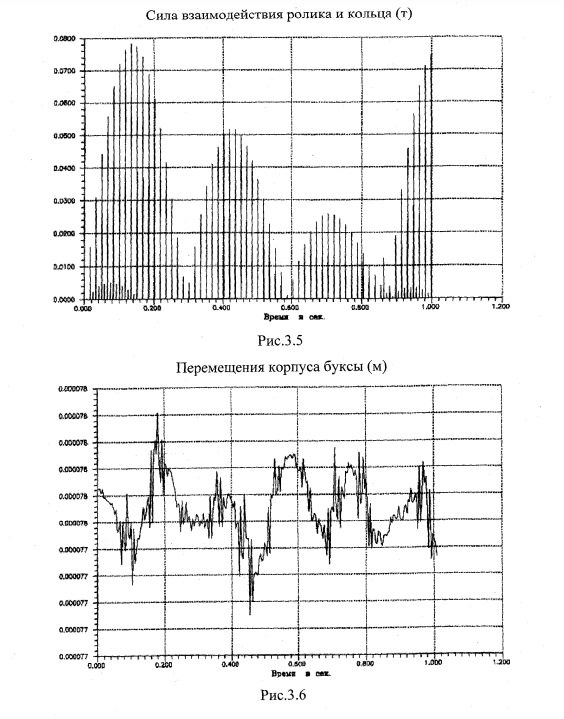
На рис.3.5-3.7 показаны фрагменты расчетов, когда трещина имеет ширину 2 мм.
Соответственно на этих рисунках показаны:
- сила взаимодействия ролика и кольца (рис.3.5);
- перемещения корпуса буксы (рис.3.6);
- модуль вертикального ускорения корпуса буксы (рис.3.7).
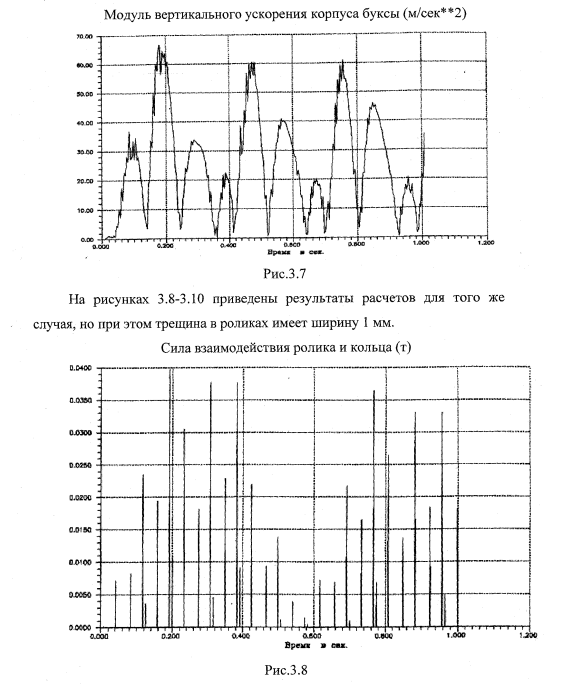
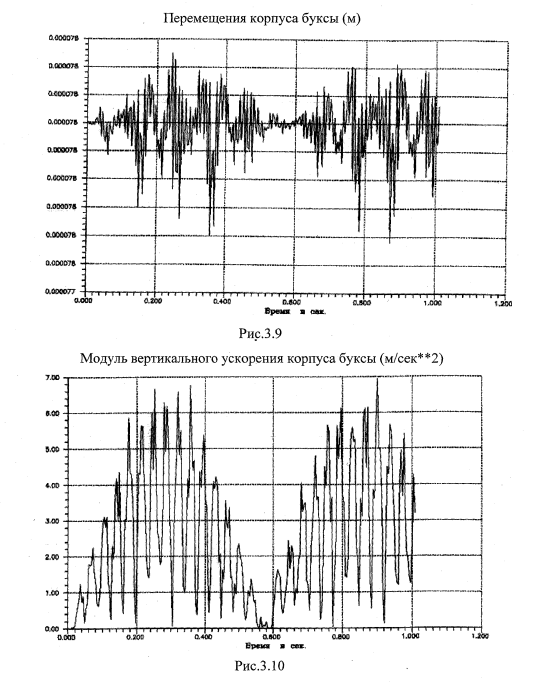
В заключение этого раздела можно отметить, что разработанная программа расчета системы «колесная пара-стенд» дает информацию для создания анализирующей системы контроля неисправностей подшипников.
Эта информация содержит собственный частотный спектр, эффективные частоты и амплитуды ускорений, вызванных повреждениями подшипников.
Выводы по главе 3
- Для создания системы анализа неисправностей подшипников в диссертации разработана компьютерная программа, позволяющая:
- определять спектр собственных частот и собственные формы колебаний системы «колесная пара с буксами-стенд»;
- вычислять начальные условия интегрирования, представляющие статические перемещения расчетных узлов колесной пары на стенде под действием собственного веса;
- проводить численное интегрирование дифференциальных уравнений модели, в результате которого определяются эффективные частоты упругих вибраций и амплитуды перемещений, скоростей и ускорений.
2. Расчетный спектр собственных частот упругих колебаний колесной пары на стенде лежит в пределах 50 гц-50 Кгц.
3. Большинство повреждений подшипников может в математической
модели имитироваться в виде периодических импульсных воздействий. В виде таких воздействий могут моделироваться трещины в роликах, кольцах и сепараторах, раковины, электроожоги и другие.
Список литературы
- Ивович В.А. Переходные матрицы в динамике упругих систем. М., «Машиностроение», 1969,199 с.
- Инструктивные указания по эксплуатации и ремонту вагонных букс с роликовыми подшипниками. МПС-ВНИИЖТ, М., «Транспорт», 1985, 160 с.
- Калиткин H.H. Численные методы. М., «Наука», 1978, 512 с.
- Карман Т., Био М. Математические методы в инженерном деле. M.-JL, «Гостехиздат», 1948, 415 с.
- Крылов А.Н. Вибрация судов. М.-Л., ОНТИ, 1948, 403 с.
- Каудерер Г. Нелинейная механика. М., И.Л., 1961, 778 с.
- Квасов В.И. Исследование контактных давлений в буксовых подшипниках качения с цилиндрическими роликами. Автореферат диссертации на соискание ученой степени кандидата технических наук. Ростов-на-Дону, 1973, 22 с.
- Классификация и каталог дефектов и повреждений подшипников качения. МПС, М., «Транспорт», 1976, 63 с.
- Кудрявцев H.H. Исследование динамики необрессоренных масс. Труды ВНИИЖТ, вып. 287. М., «Транспорт», 1965, 168 с.
- Куликов А.Б., Хусидов В.Д., Петров Г.И., Хусидов В.В. Математическая модель диагностики подшипников вагонных букс. Тезисы докладов научно-технической конференции «Подвижной состав 21 века (идеи, требования, проекты)», С.-Петербург, 1999, с. 106-108.
- Лазарян В.А. Динамика вагонов. М., «Трансжелдориздат», 1964,
255 с. - Ландау Л.Д., Лифшиц Е.М. Теория упругости. 3-е издание, М., «Наука», 1965, 202 с.
- Ляпунов A.M. Общая задача об устойчивости движения. М.-Л., «Гостехтеориздат», 1950, 471 с.
- Малкин И.Г. Теория устойчивости движения. М., «Наука», 1968,
532 с.