Моделирование напряженного состояния при волочении заготовки н^ размер под профилирование

Оглавление

Toggle

Цикл статей:
Глава 1 – Повышение качества и конкурентоспособности высокопрочной арматуры диаметром 10,0 мм для железобетонных шпал на основе разработки рациональных режимов холодной деформации и термической обработки

Глава 2 – Моделирование напряженного состояния при волочении заготовки н^ размер под профилирование

Глава 3 – Разработка модели управления геометрическими показателями качества арматуры при профилировании

Глава 4 – Исследование формирования качества арматуры периодического профиля термическим упрочнением с отдельного нагрева

Глава 5 – Разработка рациональных режимов формирования заданного уровня качества высокопрочной арматуры для железобетонных шпал и реализа­ция результатов работы в промышленности

Определение диаметра заготовки под профилирование

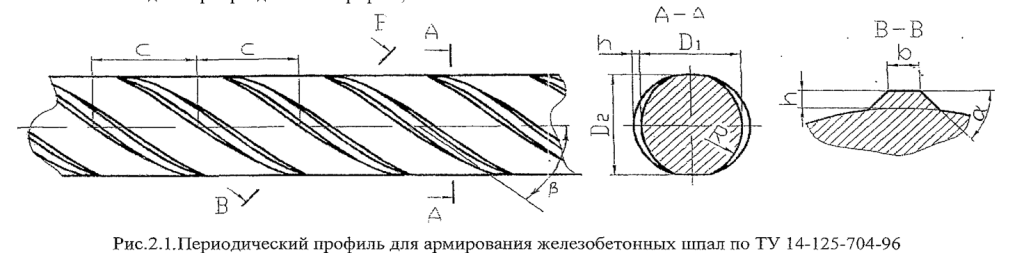
При нанесении периодического профиля на поверхность круглой заго­товки необходимо обеспечить получение арматуры требуемого номинально­го диаметра с заданным уровнем сцепления и минимальной массой погонно­го метра. Выполнение этих требований зависит от соотношений между пара­метрами периодического профиля и размера заготовки под профилирование. В табл. 2.1 приведены требования к геометрическим показателям качества периодического профиля (рис.2.1) для армирования железобетонных шпал по ТУ 14-125-704-96. Для определение диаметра заготовки под профилирование воспользо­вались универсальной методикой и инженерной формулой, полученной в ра­боте [60].

¿1 = /4- / ■(} -¿ + £/²

0 V о г н                                 н ,

k-Sr-sm.fi

где ¿г ^ ^ – критерий Рема, характеризующий сцепление арма-

туры с бетоном вне зависимости от вида периодического профиля;

– площадь проекции выступа конкретной конфигурации на плоскость, перпендикулярную продольной оси арматурного стержня (рис.2.2 ), мм²; /3 – угол наклона выступа к продольной оси стержня, град; X – шаг периодических выступов на поверхности стержня, мм; к- число выступов на периметре стержня; ТУ1 – масса арматурного профиля, г; I – длина арматурного профиля, мм;

Номи­нальный диаметр, мм	Площадь сечения, мм2	Линейная плотность г/м	Общие размеры профиля			Размеры, угол наклона анкерующих выступов
			01, мм	Р2, мм	К, мм	Ь, мм	в, мм	с, мм	Р,град
10	77,75+5%	610±5%	+0,3 9,3 -0,2	+0,3 10,2 -0,2	5,8	0,6+0,1	1,0	ю.,	30
	(73,8-81,6)	(580-640)	(9,0-9,5)	(9,9-10,4)		(0,5-0,7)		(9-10)

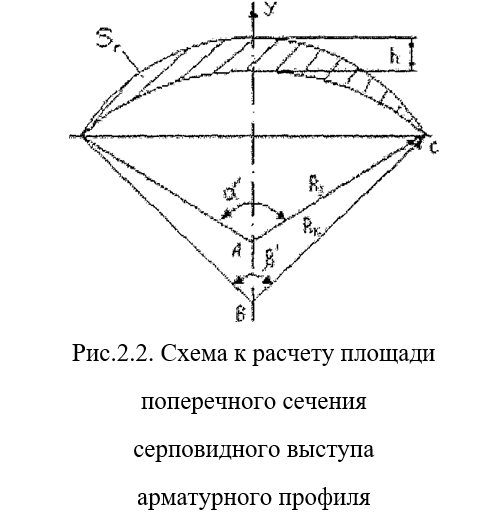
Площадь проекции серповидного выступа арматурного профиля на плоскость, перпендикулярную продольной оси арматурного стержня опреде­лится из выражения:

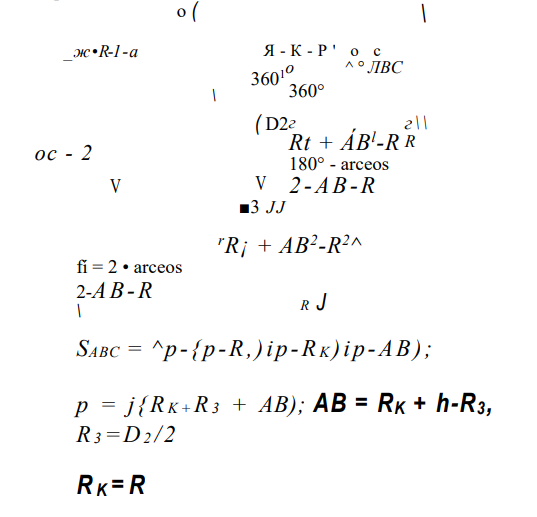
В полученной формуле номинальный диаметр является функцией ме­таллоемкости элементов периодического профиля и основного сечения арма­турного профиля. Масса прутка периодического профиля определяется из выражения:

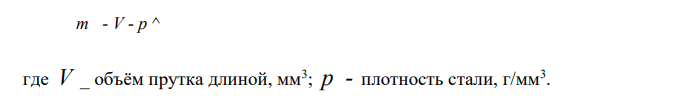
Объём прутка периодического профиля складывается из объёма основ­ной части прутка и объёмов выступов на произвольной длине:

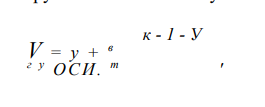
Полный объём одного выступа рассчитывается:

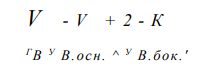
Рассчитаем объём одного серповидного выступа. В поперечном сече­нии выступ условно представим состоящим из двух блоков (рис. 2.3). Объем основного тела выступа определится из выражения:

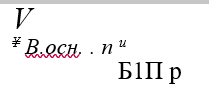
где Ь – ширина анкерующего выступа.

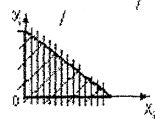
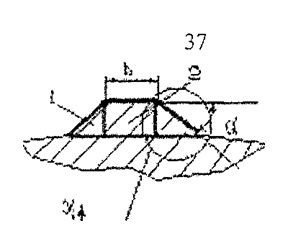
Рис. 2.3. К определению объема выступа периодического профиля 1-боковые участки, 2-основное тело выступа

Для расчета объёма боковых участков выступа рассмотрим его попе­речное сечение и его боковой участок, который имеет вид прямоугольного треугольника рис. 2.3. В поперечном сечении с определенным шагом, прове­дем секущие плоскости в фронтальной части выступа, которые при пересе­чении боковой грани выступа, будут иметь серповидный вид. Эти площади рассчитываются следующим образом:

АВ, = Я_к + у, – Я,

где У\ высота текущего сечения

Так как поперечное сечение бокового участка выступа имеет форму прямоугольного треугольника, то текущую ординату можно определить по формуле:

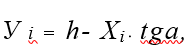
Интегрируя (2.12) вдоль линий скольжения & и £ получим

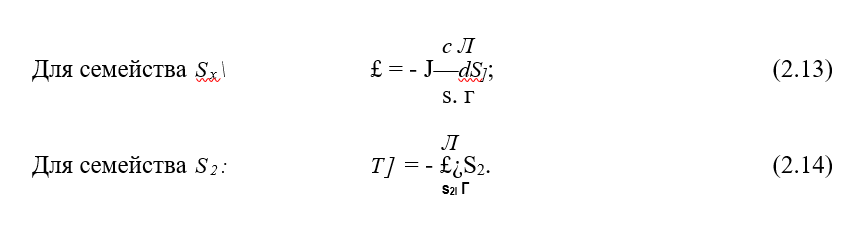
Сетка линий скольжения в меридиональном сечении (рис. 2.4) по­строена с использованием свойств линий скольжения и численного метода решения краевой задачи Римана. Сетка линий скольжения состоит из тре­угольной области ABC, примыкающей к контактной поверхности, двух цен­трированных вееров ACD, ВСЕ и криволинейной области CDOE. Сетка ли­ний скольжения ограничивает очаг пластической деформации.

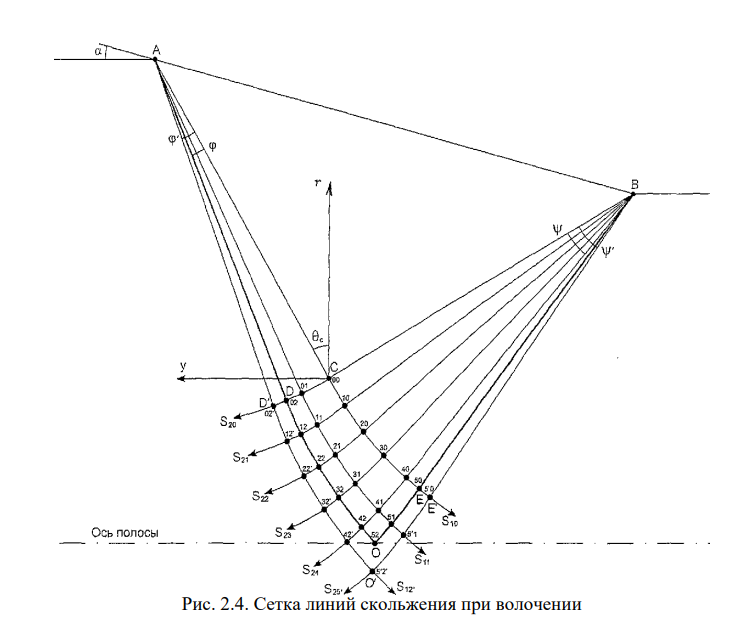
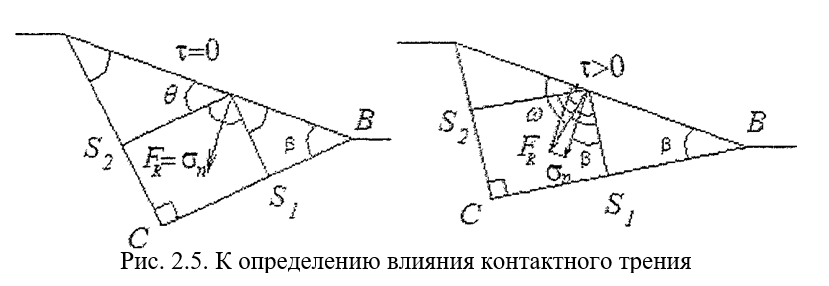
В области ABC, примыкающей к контактной поверхности, линии скольжения представляют собой два семейства взаимно перпендикулярных прямых. Согласно второму уравнению системы (2.5) всюду вдоль линии скольжения <т – к COS 26, в том числе и на поверхности тела. Поэтому, ес­ли в предельном случае трение на контакте отсутствует, то F_R – равнодейст­вующая сил, действующих на контактной поверхности, совпадает с <т_и и перпендикулярна образующей волоки, а линии скольжения обоих семейств выходят на контактную поверхность под углом 45°.

Если на поверхности контакта металла с инструментом касательные напряжения максимальны т_к = то линия скольжения семейства о, пер­пендикулярна к контактной поверхности, а линия семейства касательная к ней и угол между образующей волоки и составляет аг^ —. Поэтому, если на поверхности имеет место трение скольжения (0< т_к <—) и принимается закон трения Амонтона т_к – /(7_п, то линии скольжения семейства выходят на поверхность углами ^ > в > О (рис. 2.5).

При варьировании Т_к в тех же пределах мы можем наблюдать изме­нение угла наклона ^ к контактной поверхности в диапазоне п %        1

— > 0) >– агс^ —. Анализируя влияние контактного трения на угол выхода к контактной поверхности в и угол наклона к образующей волоки СО с учетом ортогональности семейств линий скольжения, было выдвинуто предположение, что угол наклона ^находиться в прямой зависимости от угла наклона линии семейства . Используя данное предположение, опре­делим численное влияние контактного трения, которое характеризуется ве­личиной угла

Из геометрических соображений (рис. 2.5) видно, что угол [3 опреде­ляется из выражения:

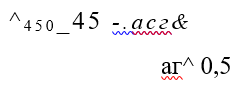
Применение закона трения Амонтона при волочении обосновано в ра­ботах [34,86] и хорошо подтверждается практикой. В работах [45,61] задача

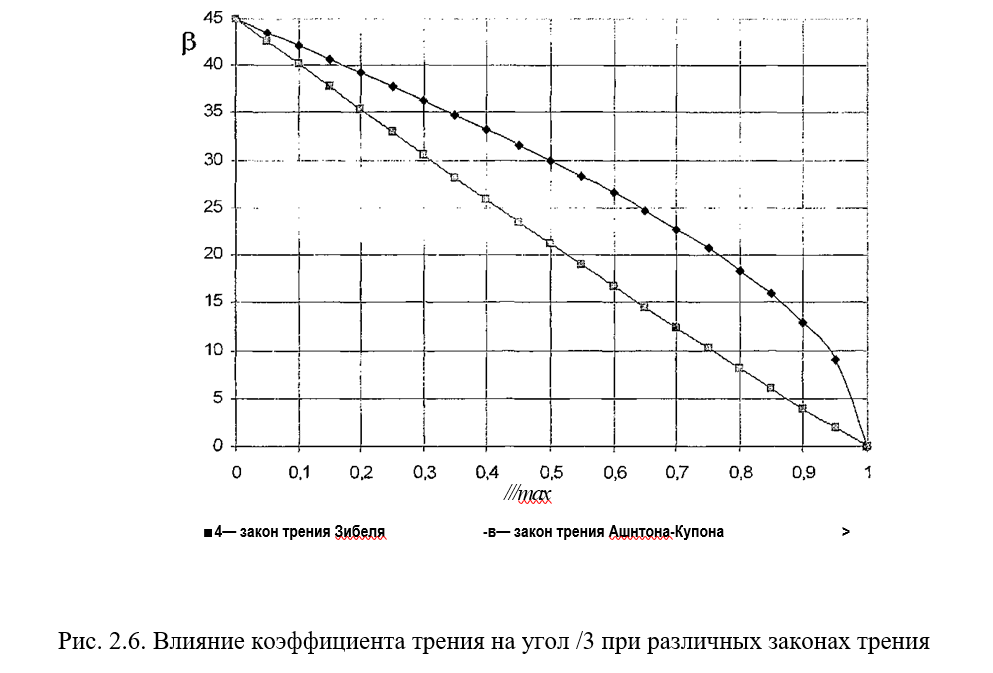
Из работы [61] следует, что при использовании закона Зибеля угол, ха­рактеризующий трение равен:

Закон трения Амонтона впервые применяется при использовании ме­тода линий скольжения, поэтому был проведен сравнительный анализ влия­ния законов трения на угол (3, который представлен на рис. 2.6.

Видно, что трение по закону Амонтона оказывает большее влияние на угол ¡3 во всем диапазоне изменения коэффициента трения /.

К треугольной области ABC со стороны катетов АС и ВС примыкают центрированные поля АСЕ и BCD, образованные лучами прямых и концен­трическими окружностями. Сетку линий скольжения в четырехугольной кри­волинейной области CDOE строим, решая по данным на дугах СЕ и CD на­чальную характеристическую задачу Римана. Точки пересечения линий скольжения назовем узловыми точками. Узловая точка «mn» образована пе­ресечением n-ой линией скольжения семейства S_] и га-ой линией скольжения семейства S₂.

После построения сетки линий скольжения находим в каждой узловой точке функции напряженного состояния £ и Т]. При этом достаточно найти одну из них так как, вычитая первое уравнение (2.8) из второго, получим:

г] = % +                                                                                                         (2.19)

ля нахождения величины % кривую OD разобьем на 100 участков. На каждом участке кривую заменим хордой. Это допущение значительно упро­щает интегрирование в (2.13, 2.14), при этом погрешность расчетов не пре­вышает 1%.

Рассматривая кривую ODA как совокупность участков прямых линий, найдем параметр проинтегрировав в качестве примера уравнение (2.13) на отрезке AD. В произвольной точке G на линии AD по формуле (2.13) имеем: rÄdS. _Р

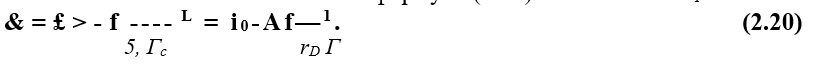
С учетом уравнения (4.10) выражение (4.20) легко интегрируется

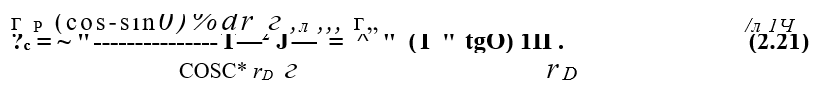
В уравнении (2.22) в итоге неизвестно <f₀ в точке О. Так как функция £ по уравнению (2.22) может быть найдена в любой узловой точке на линии ODA, то может быть найдено в каждой точке и <7 через соотношение

На линии скольжения ODA на входе в очаг деформации помимо нор­мальных напряжений действует максимальное касательное напряжение Т_тт = к. Для нахождения проецируем все силы, действующие на линии ODA на ось у и приравниваем к противонатяжению, которое принимаем равным нулю. Уравнение равновесия сил при отсутствии противонатяжения принимает вид:

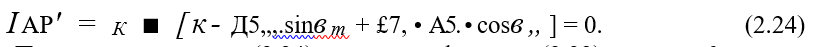
После вычисления по (2.24), используя формулу (2.22) находим £

во всех узловых точках линии ODA. Затем, интегрируя (2.13, 2.14), находим ^ и во всех остальных точках сетки линий скольжения. Зная функции и ¡7 во всех узловых точках сетки по (2.23) и (2.5) находим компоненты тензора напряжений о_п, <J_yy, (J_ry.

Описанный выше алгоритм позволяет рассчитать напряжения и опре­делить границы зон с разными схемами напряженного состояния в очаге де­формации при волочении в зависимости от технологических факторов про­цесса.

Влияние технологических факторов на напряженное состояние

Методика расчета напряженного состояния с использованием метода ли­ний скольжения требует большого объёма графических построений и мате­матических вычислений, поэтому с целью автоматизации расчетов и по­строения полей напряжений очаге деформации был разработан программный продукт «Автоматизированный расчет напряженного состояния при волоче­нии» на языке «Delphi» (подана заявка на регистрацию программы в Феде­ральный орган исполнительной власти по интеллектуальной собственности). Программа имеет понятный интерфейс (рис.2.7.) и доступна пользова­телям, не имеющим специальной подготовки, легко вписывается в систему управления качеством продукции. Разработанный программный продукт по­зволяет оперативно моделировать и оценивать уровень напряженного со­стояния при волочении в зависимости от технологических факторов обработ­ки и показывать визуальную картину распределения напряжений в очаге де­формации (рис. 2.8-2.9).

На базе программы выполнили анализ влияния технологических фак­торов волочения на распределение напряжений по сечению проволоки. На рис. 2.10-2.12 показано распределение напряжений <7_п и <7_уу вдоль грани­цы поля линий скольжения на входе в очаг деформации, в связи с наиболь­шей неравномерностью распределения напряжений, и влияние на него раз­личных факторов – степени деформации, угла волоки и контактного трения. Анализируя полученные данные видно, что продольные напряжения сг , растягивающие в центральной части очага деформации и сжимающие в кон­тактной области. С учетом знака они уменьшаются от оси к контактной по­верхности и увеличиваются от входного сечения к выходному.

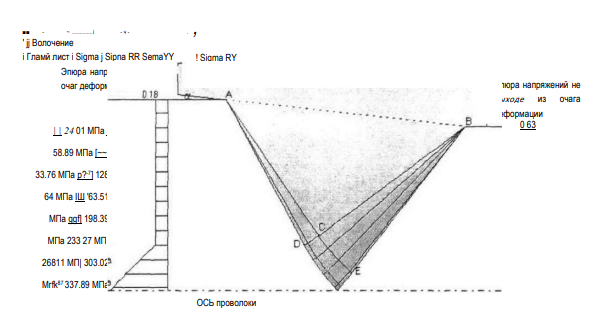
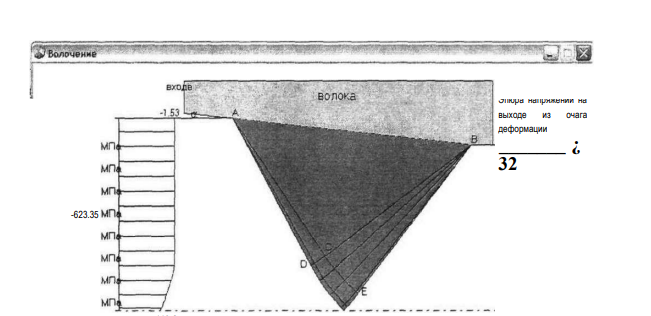
Рис.2.8. Результаты расчета волочения заготовки под профилирование а- поле продольных напряжений а_к> ; б – поле радиальных напряжений <7 (при 8=25%, полуугол волоки-6⁰)

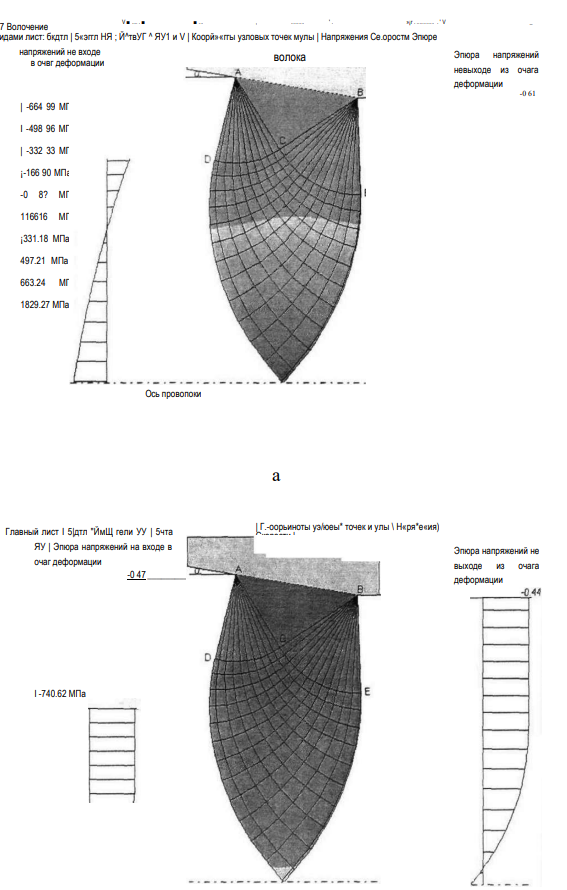
Рис. 2.9. Результаты расчета волочения заготовки под профилирование а- поле продольных напряжений сг^ ; б – поле радиальных напряжений <т (при £=12%, полуугол волоки-6⁰)

Радиальные напряжения <7_гг, преимущественно сжимающие по всему очагу деформации. По абсолютной величине они уменьшаются от контакт­ной поверхности к оси и от входного сечения к выходному.

Таким образом, наиболее неблагоприятное напряженное состояние имеет место на оси проволоки, где максимальны с учетом знака и продоль­ные, и радиальные напряжения.

Неравномерность распределения напряжений по сечению проволоки с уменьшением степени деформации возрастает (рис. 2.10). Продольные на­пряжения ст являются растягивающими на оси проволоки при любых сте­пенях деформации. Причём, с уменьшением степени деформации они увели­чиваются. При малых степенях деформации поверхностные слои проволоки у входа в волоку оказываются сжатыми в продольном направлении <7 < 0).Радиальные напряжения <7_гг с учетом знака уменьшаются от оси

проволоки к поверхности, где имеют максимум по абсолютной величине. Причем, при больших степенях деформации радиальные напряжения на оси проволоки сжимающие, а при малых степенях деформации – растягивающие. Таким образом, при определенных параметрах процесса волочения в цен­тральных слоях проволоки может возникнуть неблагоприятная зона напря­женного состояния всестороннего растяжения.

Из рис. 2.10 видно, что чем меньше степень деформации, тем больше растягивающие напряжения, и больше протяженность зоны всестороннего растяжения.

Увеличение угла волоки действует аналогично уменьшению степени деформации (рис. 2.11). Чем больше угол волоки, тем больше неравномер­ность напряженного состояния. С увеличением угла волоки радиальное на­пряжение <7_п растет по всему сечению. Продольное напряжение (Т_уу при этом увеличивается на оси проволоки, а у поверхности убывает и достигает даже отрицательного значения.

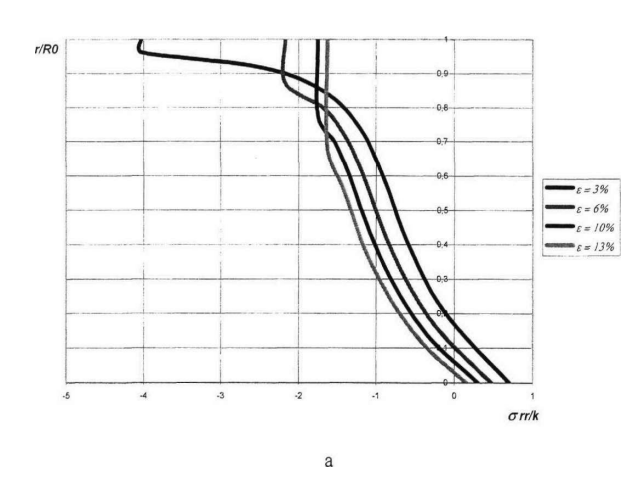
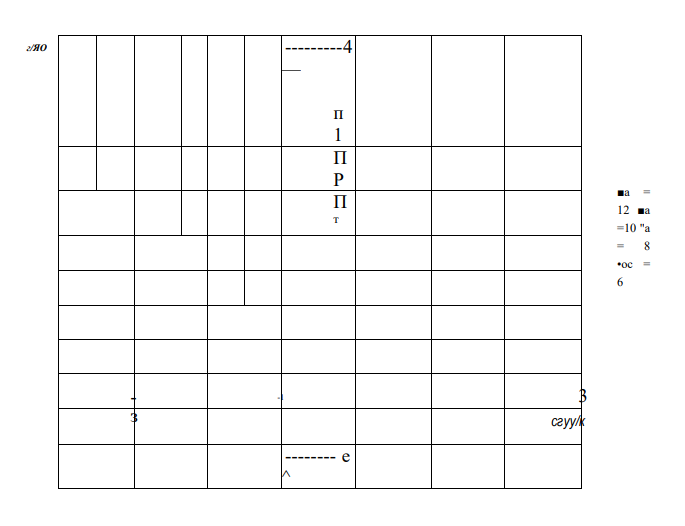
Рис. 2.11. Распределение напряжений С7_п (а) и СТ_уу (б) на входе в очаг дефор­мации в зависимости от полуугла волоки при £ = 13% и / = 0,06

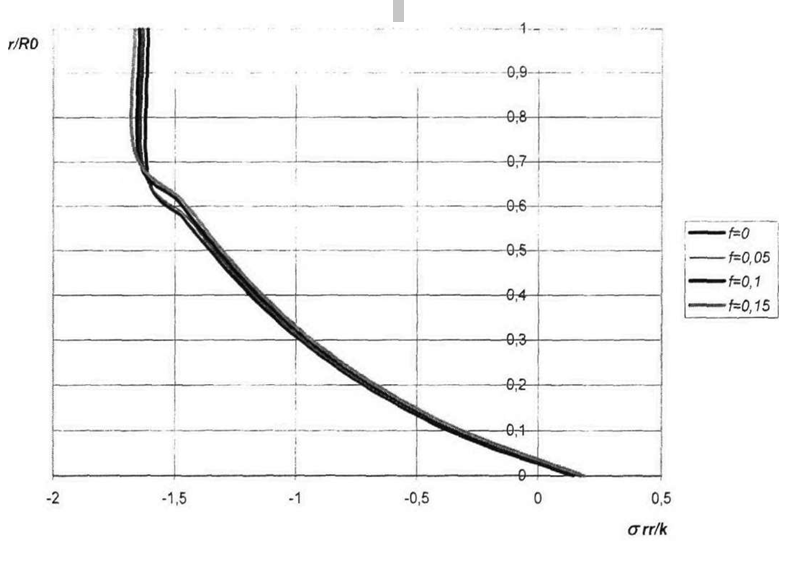
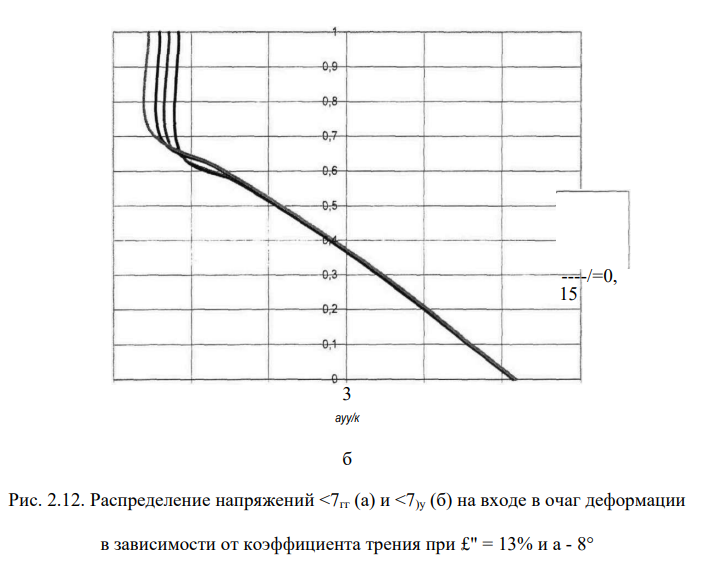
Контактное трение оказывает сравнительно слабое влияние на напря­женное состояние (рис. 2.12). С увеличением трения на контакте неравно­мерность напряженного состояния возрастает.

С увеличением коэффициента трения радиальное напряжение растет по всему сечению, а продольное напряжение на оси увеличивается и убывает к поверхности проволоки. Однако при реально существующих коэффициентах трения / = 0,02 ОД все эти изменения невелики. Таким образом, увеличе­ние контактного трения действует аналогично уменьшению степени дефор­мации и увеличению угла волоки.

Анализируя полученные результаты, можно сделать вывод, что при не­которых параметрах процесса волочения в центре очага деформации имеется зона напряженного состояния всестороннего растяжения. Протяженность её по радиусу проволоки и действующие в ней растягивающие напряжения (7_п. и <7 тем больше, чем меньше степень деформации, больше угол волоки и

контактное трение. Напряженное состояние всестороннего растяжения явля­ется весьма неблагоприятным для материала протягиваемой проволоки. В за­висимости от материала, его структуры, параметров обработки наличие зоны всестороннего растяжения может проявлять себя по разному во внутренней области изделия. В одних случаях могут образовываться внутренние дефекты в проволоке, в других только понижаться твердость и наблюдаться явление «разрыхления» [63].

Для характеристики напряженного состояния и оценки рационально­сти назначаемых режимов обработки введем коэффициенты тип. Коэф­фициент т характеризует протяженность зоны напряженного состояния все­стороннего растяжения в радиальном направлении:

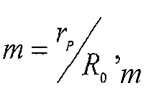
где г_р – радиус, до которого действуют радиальные растягивающие напряже­ния, Я₀ – начальный радиус.
С уменьшением степени деформации и увеличением угла волоки ко­эффициент т увеличивается, а напряженное состояние продукта волочения становится неблагоприятным для последующего профилирования и термиче­ской обработки. (рис. 2.13).

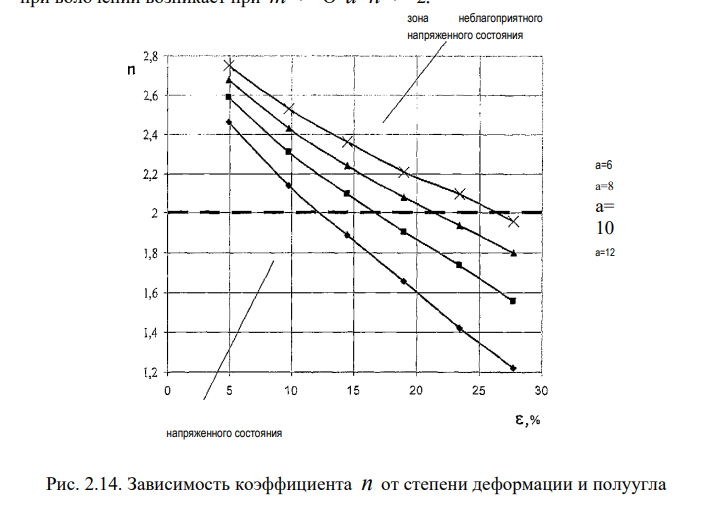
Максимальное растягивающее напряжение действует на оси проволо­ки, в точке О, и является продольным напряжением. Коэффициент п (рис.2.14) позволяет судить о вероятности возникновения дефектов в прово­локе. На оси проволоки, в точке О, сг, = <т , а <т₃ = (7_п.. Тогда из условия пластичности (2.1) получим а =2к + <7_гг. Следовательно, при растягиваю­щем радиальном напряжении с_п > 0 продольное напряжения ст превыша­ет предел текучести, а коэффициент п>2. Итак, неблагоприятное напря­женное состояние при волочении возникает при т > О и п > 2.

Полученные результаты использованы при проектировании режимов волочения заготовки под профилирование.

Выводы

1. Получена инженерная формула, позволяющая определять диаметр круглой заготовки под профилирование арматурного периодического профи­ля по ТУ 14-125-704-96 из учета получения требуемого уровня сцепления с бетоном и минимальной массы погонного метра профиля.
2. На основе метода линий скольжения выполнен анализ напряженно­го состояния в очаге деформации при волочении заготовки под профилиро­вание. Показано влияние основных технологических факторов процесса во­лочения на распределение напряжений в очаге деформации. Для анализа влияния технологических параметров волочения на вероятность возникнове­ния неблагоприятного напряженного состояния предложены коэффициенты тип, характеризующие соответственно размеры зоны всестороннего рас­тяжения и отношение максимального растягивающего напряжения в очаге деформации к пределу текучести обрабатываемой стали.
3. Разработано программное обеспечение расчета напряженного со­стояния в очаге деформации при волочении методом линий скольжения, с помощью которого возможно оперативно моделировать и анализировать ус­ловия деформирования в зависимости от технологических факторов процесса и исходной заготовки с учетом особенностей последующего профилирования и термической обработки.

Список литературы

1. В.В Битков Технология и машины производства проволоки.- УРО РАН, Екатеринбург, 2004., 368С.
2. Зубов В.Я. , Мальцева Л.А. О масштабном факторе при разрушении стальной проволоки //. Термическая обработка и физика металлов. Вып.2. -Свердловск: УПИ, 1976. С. 15-19.
3. Семавина А.Н., Гаврилюк В.Г., Терских С.А. О природе масштабного эффекта в холоднотянутой стальной проволоке // Физико-химическая механика материалов.- 1979.- №2.-С. 24-28.
4. Р.Б. Красильщиков. Деформационный нагрев и производительность волочильного оборудования.- М: Металлургия, 1970, 218 С.
5. Э. Штольте., В. Геллер. Самозакаливающаяся арматурная сталь с улучшенными эксплуатационными свойствами//Черные металлы- №1.- 1974.- С.11-14.
6. Закалка с высоким отпуском пружинной проволоки// Новости черной металлургии за рубежом – №3.- 2005.-С. 48-49.
7. И.А. Юхвец. Производство высокопрочной проволочной арматуры- М.: Металлургия, 1973, 324С.
8. Фогель Л. М. Повышение свойств арматурной проволоки с четырех-сторонним профилем на основе совершенствования режимов волочения и про-филирования. Дис. канд. техн. наук.- Магнитогорск: МГМИ, 1991, 138С.
9. Киреев Е.М. Совершенствование производства высокопрочной арма-турной проволоки с целью повышения ее релаксационной стойкости. Дис. канд. техн. наук.- Магнитогорск: МГМИ, 1984, 146С.
10. Харитонов В.А. Исследование и разработка способа производства вы-сокопрочной арматурной проволоки прокаткой в трехвалковых калибрах: Дис. канд. техн. наук.- Магнитогорск: МГМИ, 1975Д35С.
11. Харитонов В. А Повышение эффективности производства пружинной и арматурной проволоки диаметром 6,0 -8,0 мм холодной прокаткой в трехвал¬ковых калибрах: Дис. канд. техн. наук.- Магнитогорск: МГМИ, 1988, 138С.
12. Белан А.К. Исследование и разработка технологии изготовления низ-коуглеродистой арматурной проволоки прокаткой в многовалковых калибрах. Дис. канд. техн. наук.- Магнитогорск: МГМИ, 1981,172С.
13. Г. JI. Горелик, A.M. Тельтейбаум. Новые виды высокопрочной проволоки для производства железобетонных шпал// Бетон и железобетон .- № 4.- 1991.-С.14-16.
14. Высокопрочная арматурная сталь / Кугушин A.A., Узлов И.Г., Калмы¬ков В.В., Мадатян С.А., Ивченко A.B. – М.: Металлургия, 1986, 272С.
15. Сычков А.Б., Жигарев М.А., Перчаткин A.B. Высокопрочный арма¬турный прокат из высокоуглеродистой стали// Вестник МГТУ им.Г.И. Носова.- 2005.-№ 1.-С.42-45.
16. С.А. Мадатян. Арматура железобетонных конструкций.-М.: Воентех- лит, 2000, 256 С.
17. Мадатян С.А. Новое поколение арматуры железобетонных конструк¬ций // Бетон и железобетон. – 1998. – №2.-С. 3-6.
18. Баскин С. Л. Арматурные профили малых сечений для сборного желе-зобетона//Сталь. – 1987.- № 10.-С. 12-16.
19. В.А. Шеремет. Проблемы производства бунтового проката с заданными физико-механическими свойствами// Труды шестого конгресса прокатчиков., М.: Черметинформация, 2006.- Т.1.-С. 135-136.
20. Рахштадт А.Г. . Пружинные стали и сплавы. М.: Металлургия, 1982,
    400 С.